Использование метода для решения задачи

Обоснование и выбор метода решения

Данная задача принадлежит к типу задач квадратичного программирования. Это частный случай задачи нелинейного программирования.

Вообще, основной недостаток методов нелинейного программирования заключается в том, что с их помощью не удается найти глобальный экстремум при наличии нескольких локальных экстремумов. Поэтому метод считается теоретически разработанным, если найдены соотношения, являющиеся необходимыми и достаточными условиями оптимума, и алгоритмы поиска экстремума с доказательством их сходимости. Этим требованиям удовлетворяют только методы, рассматриваемые в разделе квадратичного программирования, частично методы решения задач с сепарабельными функциями и в значительно меньшей степени прямые методы.

Задача нелинейного программирования.

Рассмотрим задачу математического программирования:

 

,                                                                (1а)

                                                                    (2а)

                                                 (3а)

, ,                                                                  (4а)

 

здесь F(x) - целевая функция, выражение (2) - ограничения равенства, выражение (3) - ограничения неравенства, x - вектор переменных, D_j - некоторые множества.

Если хотя бы одна из функций F(x), φ_i(x) - нелинейная, то это модель задачи нелинейного программирования. Решение подобных задач возможно только для некоторых классов функций F(x), φ_i(x), и когда D_j - множество действительных чисел

Задача квадратичного программирования = частный случай задачи нелинейного программирования, в которой целевая функция = сумма линейной и квадратичной функции, а все ограничения линейны:

 

,           (5а)

,                                          (6а)

                                                                          (7а)

 

или в матричном виде (P,x,B - векторы-столбцы):

 

,                                         (8а)

,                                                                                     (9а)

                                                                                                  (10а)

 

В выражении (8а) матрица С должна быть симметричной и положительно полуопределенной - это гарантирует выпуклость целевой функции (5а). Известно, что для задачи выпуклого нелинейного программирования справедлива теорема Куна-Таккера, выражающая необходимые условия того, что точка x₀ является решением задачи нелинейного программирования:

 

                                                                                                            (11а)

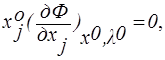
                                                                                                            (12а)

 

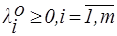
где Ф=Ф(x,λ) - функция Лагранжа.

Теоретически наиболее широко и детально в нелинейном программировании разработан раздел выпуклого программирования, называемый квадратичным.

Методы квадратичного программирования можно разделить на три группы:

-   Алгоритмы, использующие симплекс-метод;

-   Градиентные методы;

    Прочие специальные методы.

К первой группе можно отнести метод Баранкина и Дорфмана. Для поиска опорного решения в нашей задаче мы будем использовать именно его, т.к. данная целевая функция представляет собой сумму линейной и квадратичной функции, а все ограничения линейные.

Метод Баранкина-Дорфмана

Задача формулируется следующим образом (в матричном виде):

 

P’x+x’Cx -> min,£ b,

x ³ 0

 

Исходя из теоремы Куна-Таккера, обозначим:

 

 

В данном случае условия Куна - Таккера запишутся в виде:

 

Ax + y = b;                                                                        (1)

Cx - v + A’l = -p;                                                              (2)

x ³ 0, Y ³ 0, V ³ 0, l ³ 0;                                                   (3)+ Yl = 0. (4)

 

Отметим, что последнее равенство (4) может выполняться только для допустимого базисного решения системы, которое характеризуется той особенностью, что из

(n + m) ограниченных по знаку переменных x, V, Y, l самое большое N переменных, где N = n + m - число равенств в этой системе, отличны от нуля.

Идея метода Баранкина и Дорфмана заключается в том, что процедура последовательного отыскания решения начинается с базисного решения системы (1)-(3), которое не обязательно удовлетворяет условию (4). Затем с использованием симплекс-метода добиваются равенства нулю выпуклой функции xv + yl.

а) алгоритм:

Для удобства изложения все переменные представим в виде 2N - мерного вектора

= ||x,y,v, l||.

 

Можно поставить в соответствии каждому вектору z вектор z’, определяемый соотношением

’ = ||v, l,x,y||,

 

такой, что

 

z’_I=z_i+N, z’_I+N=z_i, = 1,2,..,N,

xV+Yl = 1/2zz’.

 

С помощью этих векторов, условия (1) - (4) запишутся в виде:

 

  (5)(z) = zz’ = 0, z ³ 0.

 

Исходя из некоторого допустимого базисного решения системы (5), совершим последовательность симплекс преобразований, с помощью которых будем уменьшать выпуклую функцию T(z) = zz’, пока не достигнем значения T = 0.

Допустим, имеется некоторое допустимое базисное решение системы (5). Симплекс - таблица в данном случае должна задавать входящие в базис переменные z_g как функцию от N небазисных переменных z_vh=t_h, не входящих в базис:

 

, g=1,2,..,2N.   (6)

 

эту запись можно использовать и для небазисных переменных из числа z_g. Для этого симплекс-таблица дополняется строками, все элементы которой (кроме одного, равного единице) равны нулю. В этих строках для небазисной переменной z_{g =} t_j будет d_gh = 0, h =j, a d_gj = 1. функциональную зависимость (6) можно записать в векторном виде:

 

 . (7)

 

При небазисных переменных t_h = 0 формула (7) перепишется в виде

= d₀ ≥ 0, T=d₀d’₀.

 

Далее t_j=θ>0 и z = d₀+ θd_j. Увеличиваем переменную t_j пока некоторая j-ая из базисных переменных не обратится в нуль. Она определяется из условия:

 

 

при d_gi<0.

Тогда новое базисное решение: z’ = d₀ + θ_id_j, а величина T соответственно

_j = T + θ_jk_j,

 

где K_j=2α_j+ θ_jβ_j,

где α_j=d_jd’₀ и β_j=d_jd’_j.

 

Очевидно, что k_j<0. Если таких несколько, то выбирается то, которому соответствует наименьшее отрицательное произведение θ_jk_j.

б) вычислительная схема

После определения допустимого базисного решения строят симплексную и дополнительную таблицы в виде табл.1.

 

Таблица 1.

 

В отличие от стандартной симплекс-таблицы здесь добавлена таблица для дополнительных переменных α _0, α _j, βj, θj, k_j, которые вычисляются по следующим формулам:

 

α ₀ = T = d₀d’₀=2∑d_i0d_i+N,0

 

При α ₀ = 0 сразу получаем оптимальное решение. В противном случае дополнительно находим:

 

α _j = ∑(d_ijd_i+N,0 + d_i+N,jd_i,0), j = 1,…,N.

 

Далее для j, для которых α _j < 0, определяются:

 

β_j = 2∑d_ijd_i+N,j;

 при d_gj < 0.

Для определения элемента j вычисляются:

_j = 2 α _j + β_jθ_j.

 

В качестве заменяющего столбца выбирается такой, для которого отрицательное произведение θ_j K_j наименьшее. Элемент d_gj, по которому определено θ_j, становится опорным, и из базиса удаляется соответствующая ему g-я переменная, которая встает на место переменной заменяющего столбца. Затем все его элементы делятся на опорный, который при этом становится равным единице. Тем самым получаем заменяющий столбец с новыми элементами. Для получения остальных столбцов новой таблицы, из соответствующих столбцов старой вычитаем уже построенный заменяющий столбец, умноженный на элемент, стоящий на пересечении преобразуемого столбца старой таблицы и заменяющей строки.

Использование метода для решения задачи

 

В настоящее время подобные задачи легко решаются при помощи современных ЭВМ. Для решения данной задачи воспользуемся пакетом программ Gino. Но прежде решим ее вручную.

Решение задачи.

Поиск решения задачи начинается с приведения составленной целевой функции к минимуму:

 

L’ = 1.5p₁² -8500p₁ + 2.1p₂² - 7900p₂ + 0.67p₃² - 13200p₃-> min

 

)-1.5p₁+9500 £ 4900;

)-2.1p₂+7900 £ 5100;

)-0.67p₃+13200 £ 11300;

)-1.5p₁-2.1p₂-0.67p₃+29600 £ 15000;

)p₁ ³ 0;

)p₂ ³ 0;

)p₃ ³ 0;

)V₁ ³ 0;

9)V₂ ³ 0;

)V₃ ³ 0.

Составим следующие матрицы:

 

 

n = 3, m = 4, N = 7, 2N = 14.

Матрица С выполняет требования, т.к. является симметричной и положительно полуопределенной, что гарантирует выпуклость целевой функции. Для нашей задачи из выражения (5) (см. выше) получим:

 

Откуда можно получить следующие уравнения:

 

-1.5*p1 + Y1 = -3600;

*p2 + Y2 = -2800;

*p3 +Y3 = -1900;

*p1 -2.1*p2 - 0.67*p3 + Y4 = -14600; (8)

*p1 - V1 -1.5* λ1 -1.5* λ4 = 8500;

*p2 - V2 - 2.1*λ2 - 2.1*λ4 = 7900;

*p3 - V3 - 0.67*λ3 - 0.67*λ4 = 13200.

 

Для получения допустимого базисного решения (опорного решения) можно использовать любой метод отыскания опорного решения задачи ЛП. Для системы (8) достаточно выбрать p1,p2,p3,Y1,Y2,Y3,Y4 базисными, тогда:

 

 

Значит P1 = 8500/3, P2 = 7900/4.2, P3 = 13200/1.34, Y1 = 650, Y2 = 1150, Y3 = 4800, Y4 = 200- опорное решение. Составим симплекс-таблицу, учтя, что знаки коэффициентов при свободных переменных (в отличии от симплекс-таблицы задачи ЛП) не меняются. Пустые клетки соответствуют нулевым коэффициентам.

 

Таблица 2

	1	V1	V2	V3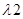
P1	8500/3	0.33			0.5			0.5
P2	7900/4.2		0.238				0.5	0.5
P3	13200/1.34			0.75			0.5	0.5
Y1	650	0.5			0.75			0.75
Y2	1150		0.5			1.05		1.05
Y3	4800			0.5			0.335	0.335
Y4	200	0.5	0.5	0.5	0.75	0.05	0.335	2.135
V1		1
V2			1
V3				1
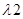1
1
1
1
α j	0
β j
Θj
Κj

 

Т.к. α₀=0, то сразу получаем оптимальное решение:

P1 = 2833.33;= 1880.95;= 9850.746;=650, Y2=1150,Y3=4800,Y4=200; =0, V2=0,V3=0;

λ1=0, λ2=0, λ3=0, λ4=0.

Поделиться:

Воспользуйтесь поиском по сайту: