Задание 4. Непараметрический коэффициент ранговой корреляции Спирмена.

Лабораторная работа № 7

Выяснение влияния факторов. Корреляционный анализ.

Задание 1. Коэффициент корреляции (параметрический):

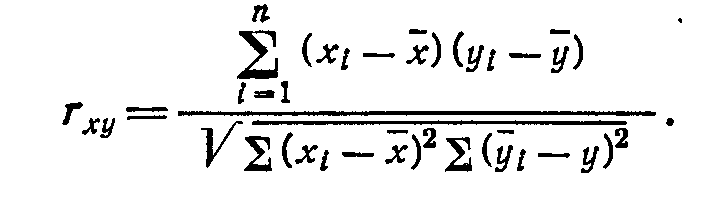
Коэффициент корреляции может принимать значения в промежутке от -1 до +1. При наличие прямой связи между варьирующими признаками коэффициент имеет положительный знак, при обратной связи – отрицательный. Если r=0, то это означает отсутствие корреляции. Коэффициент корреляции показывает степень сопряжённости между признаками и направление такой связи – чем выше значение коэффициента, тем сильнее связь, а «положительность» или «отрицательность» показывает направление такой связи. Обычно считается, что при

r < 0.3 - слабая связь,

0.3 ≤ r < 0.5 - связь умеренная,

0.5 ≤ r < 0.7 – связь значительная,

0.7 ≤ r ≤ 0.9 – связь сильная,

r > 0.9 – связь очень сильная

 

1) Исследовали жирномолочность коров и их дочерних особей, данные наблюдений занесены в таблицу:

% жира в молоке	ху	х2	у2	х-у	(х-у)2
коров (х)	дочерних особей (у)
3.10	3.65
3.17	3.11
3.76	3.57
3.61	3.61
3.27	3.44
3.61	3.71
3.80	3.61
3.65	3.98
3.34	3.36
3.65	3.89
3.45	3.45
4.05	3.79
∑

Имеется ли зависимость жирномолочности дочерних особей коров от аналогичного показателя их матерей?

Для расчета корреляции в среде Excel в строке формул найдите КОРРЕЛ или PEARSON

 

2) для малых (n < 30) выборок коэффициент корреляции рекомендуется рассчитывать с поправкой:

 

примените предлагаемую поправку для корректировки вычисленного коэффициента предыдущего задания

 

Задание 2. Вычисление ошибки коэффициента корреляции:

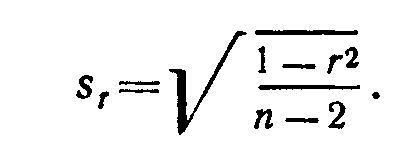
Определите ошибку коэффициента корреляции жирномолочности коров и их дочерних особей, высчитанного обычным способом и с поправкой. Сравните результаты.

 

Задание 3. Вычисление достоверности коэффициента корреляции. Проверка на достоверность полученного коэффициента корреляции можно осуществить несколькими способами, например, с помощью коэффициента Стьюдента и методом z.

1) Коэффициент Стьюдента

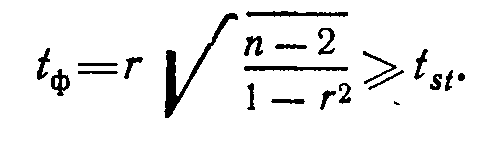
2) метод z. Данный способ применим в случае, если распределение признаков отклоняется от нормального закона (в случае с малыми выборками, например). Распределение величины z является почти неизменным по форме, т.к. мало зависит от размера выборки и величины коэффициента корреляции в генеральной совокупности.

 

1 1+r

z = ------ + ln ----------

R

 

преобразование коэффициента корреляции в величину z производится по специальной таблице.

Затем оценивается достоверность z по формуле:

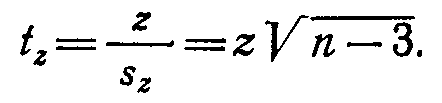
можно вычислить доверительные граници коэффициента корреляции в генеральной совокупности. Для этого сначала высчитывает погрешность z_з=tS_z при необходимом уровне значимости, определяем нижнюю и верхнюю границы z± tS_{z .}

S_z = ------------

√n - 3

3) при недостаточной достоверности z можно высчитать необходимый объём выборки для получения достоверной корреляции, что также позволяет планировать дальнейший эксперимент:

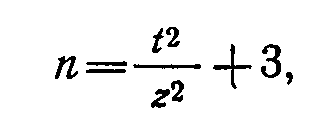
n – искомый объём выборки, t – величина, заданная по принятому уровню значимости (лучше для α=1%), z – преобразованный эмпирический коэффициент корреляции.

 

Произведите необходимые вычисления для выше указанного примера.

 

Задание 4. Непараметрический коэффициент ранговой корреляции Спирмена.

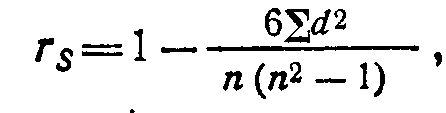
это разность между рангами сопряжённых значений х и у.

 

Для начала ранжируем значения признака х и сопряжённые с ними значения признака у (по отдельности), присваиваем им порядковые номера в соответствии с рангом. Затем определяем разность (d) рангов сопряжённых вариант (обязательно учитываем знак!), возводим её в квадрат. Подставляем в формулу.

 

оценка достоверности:

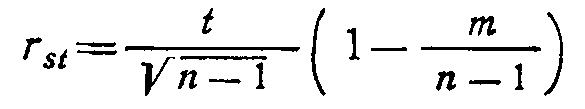
n – объём выборки; t и m – величины, связанные с уровнем значимости α следующим образом: для α=5% t =1.96 m=0.16; для α=1% t=2.58 m=0.69

 

полученный результат сравнивается с табличным.

 

для выборок n≥10 используется формула Стьюдента:

 

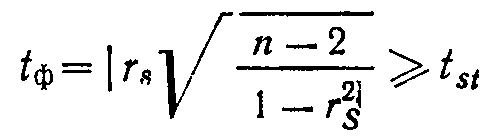
Задание 5 (домашнее). Множественная корреляция. Кроме связей двумерных совокупностей можно обнаруживать многомерные корреляционные связи. Простейшим случаем множественной корреляции является зависимость между тремя признаками: х, у, z. Тесноту связи одного из них с двумя другими измеряют с помощью коэффициента множественной корреляции:

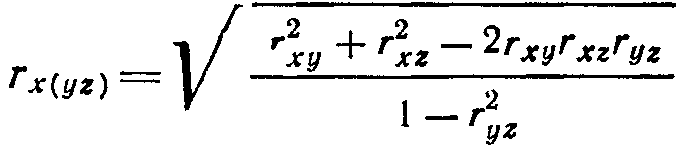
r_xy, r_xz, r_yz – коэффициенты корреляции между парами признаков.

 

В данном случае коэффициент множественной корреляции принимает значения от 0 до 1.

 

1) Из снопа озимой ржи случайным способом было отобрано 10 колосьев. Затем измерили длину каждого колоса (х), подсчитали число колосков (у) и количество зёрен в каждом колосе (z.).

 

Взаимосвязаны ли эти признаки? Укажите на степень связи.

 

Задание 6 (домашнее). Частная корреляция. Если известна связь между признаками х, у, z, то можно определить частные или парциальные коэффициенты корреляции, показывающие корреляционную зависимость между двумя варьирующими признаками при постоянной величине третьего (он берётся в скобки), его влияние временно исключается, чтобы избежать эффекта «наведения», т.е. ложной корреляции:

 

 

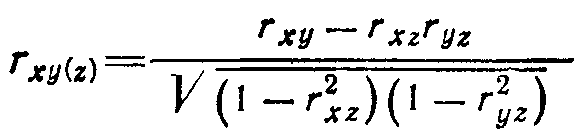
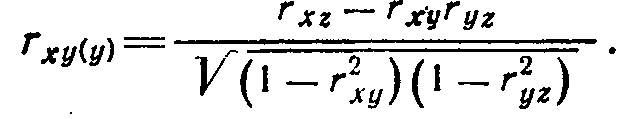
Рассмотрите корреляционную зависимость пар признаков из предыдущего задания. Какая пара признаков имеет набольшую связь? Оцените её степень достоверности.

Поделиться:

Воспользуйтесь поиском по сайту: