 |
Обработка результатов измерений
|
|
|
|
Краткая теория
Дифракцией называется…………...…………………………………………………
……………………………………..…………………….....……………………………..….
Условие наблюдения дифракции: ……………….....……………………………..…
……………………………………..…………………….....……………………………..….
Дифракция Фраунгофера – это ….…………...………………………………………
……………………………………..…………………….....……………………………..….
После прохождения нормально падающей ……………………… монохроматической волны через щель на экране наблюдается дифракционная картина, распределение интенсивности дифрагированного света показано на рисунке 1.
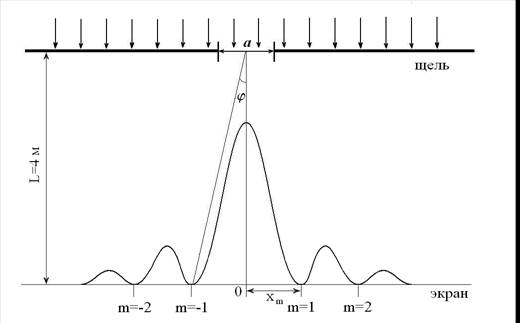
Рис. 1
Разбив фронт волны, ограниченный щелью, на зоны Френеля и определив какое количество зон N окажется в щели, можно узнать, где на экране наблюдения будут располагаться максимумы и минимумы интенсивности света.
Если N нечетное, то ………………………………… освещенность наблюдается при выполнении условия:
(3.1)
где
а – ………………………………………………………………………............................................
j – ………………………………………………………………………............................................
λ – ………………………………………………………………………............................................
m – ………………………………………………………………………...........................................
Если N четное, то ………………………………… освещенность наблюдается при выполнении условия:
(3.2)
При пропускании волны через систему из некоторого количества N (N = 2, 3, 4 …) одинаковых щелей дифракционная картина изменится (рис. 2).
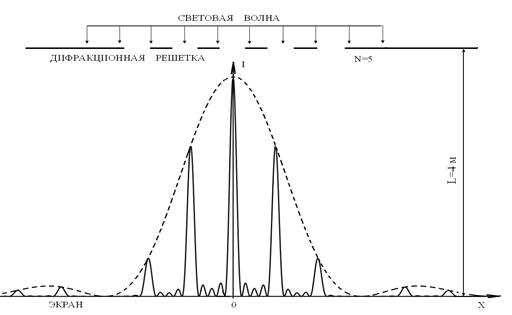
Рис. 2
Полученная картина объясняется тем, что помимо явления …………………….. происходит ………………………………………………………………………………….
……………………………………..…………………….....……………………………..….
|
|
|
…………………..……………………………………….....……………………………..….
На рис. 2 пунктирная линия – это ……………………………………………………
……………………………………..…………………….....……………………………..….
Условие наблюдения главных максимумов картины:
(3.3)
где
d – ………………………………………………………………………............................................
j – ………………………………………………………………………............................................
λ – ………………………………………………………………………............................................
k – ………………………………………………………………………...........................................
Главные минимумы – это минимумы интенсивности света, наблюдаемые ……..
……………………………………..…………………….....……………………………..….
……………………………………..…………………….....……………………………..….
……………………………………..…………………….....……………………………..….
Условие наблюдения главных минимумов картины:
(3.4)
где
a – ………………………………………………………………............................................
m – …………………...…………………………………………............................................
Между соседними главными максимумами расположено ……… добавочных минимумов и ……… добавочных максимумов очень малой интенсивности.
Условие наблюдения добавочных минимумов картины:
(3.5)
Условие наблюдения добавочных максимумов:
(3.6)
где
N – ………………………………………………………………. ..........................................
– ……………………………………………………………............................................
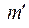С ростом числа щелей N главные максимумы становятся...……………………………………………………………………., а добавочные максимумы и минимумы ……………………………………………………………………..
……………………………………..…………………….....……………………………..….
……………………………………..…………………….....……………………………..….
Экспериментальная часть
В соответствии с порядком выполнения работы для изучения дифракции на щели необходимо выбрать заданный преподавателем цвет, задать ширину щели, измерить на экране монитора координаты x максимумов и минимумов 1, 2 и 3-го порядков и занести результаты в табл. 1.
|
|
|
Для изучения дифракции на решетке необходимо выбрать заданный преподавателем цвет и число щелей, задать период дифракционной решетки и измерить:
- координату x и порядок m одного главного максимума;
- координаты x и порядки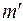 
одного добавочного минимума и одного добавочного максимума, выбранных на полученной картине между нулевым и первым главными максимумами при измененном значении периода решетки.
Результаты занести в табл. 2.
Таблица 1
| Цвет | m | а, мкм | x, мм | φ, рад | λi , мкм | <λ>, мкм | Δλ, мкм | ε, % | |
| min | |||||||||
| max | |||||||||
| min | |||||||||
| max | |||||||||
| min | |||||||||
| max |
Таблица 2
| Цвет | N | m | d, мкм | x, мм | φ, рад | λi, мкм | < λ >, мкм | Δ λ, мкм | ε, % |
| главный максимум | |||||||||
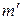
| добавочный минимум | ||||||||
|
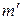
| добавочный максимум | ||||||||
L = …………… - ………………………………………………………………………
……………………………………..…………………….....……………………………..….
Студент(ка) гр. ____ _________________________________ (указать ФИО)
Дата выполнения _________ Подпись преподавателя _________________
Обработка результатов измерений
1. Для одной щели по измеренным координатам x минимумов и максимумов и известному значению L с учетом соотношения L >> x вычислить углы дифракции j (см. рис. 1):
φ = sin φ = tg φ =
m = 1 φmin = m = 1 φmax =
m = 2 φmin = m = 2 φmax =
m = 3 φmin = m = 3 φmax =
2. Вывести из формулы (3.2) и рассчитать длину световой волны по координатам минимумов для каждого порядка:
m = 1 λ1 =
m = 2 λ3 =
m = 3 λ5 =
Результаты занести в таблицу 1.
3. Вывести из формулы (3.1) и рассчитать длину световой волны по координатам максимумов для каждого порядка:
m = 1 λ2 =
m = 2 λ4 =
m = 3 λ6 =
Результаты занести в таблицу 1.
4. Вычислить среднее значение длины световой волны:
<λ> =
5. Найти отклонения λ i от среднего:
Δλ1 = Δλ2 =
Δλ3 = Δλ4 =
Δλ5 = Δλ6 =
6. Найти среднюю квадратичную погрешность:
|
|
|
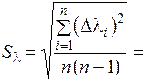
7. Задать надежность α (0,9 или 0,95) и в таблице найти коэффициент Стьюдента
tα = при α =
8. Найти абсолютную погрешность длины волны:
∆λ = tα·Sλ =
9. Найти относительную погрешность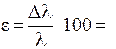 
Результаты занести в таблицу 1.
10. Для дифракции на решетке аналогично пункту 1 вычислить углы дифракции j:
φ = sin φ = tg φ =
- главный максимум m = φmax =
- добавочный минимум 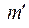= φmin =
- добавочный максимум 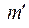= φmax =
11. Вывести из формулы (3.3) и рассчитать длину световой волны по положению главного максимума:
λ1 =
Результат занести в таблицу 2.
12. Вывести из формулы (3.5) и рассчитать длину световой волны по положению добавочного минимума:
λ2 =
Результат занести в таблицу 2.
13. Вывести из формулы (3.6) и рассчитать длину световой волны по положению добавочного максимума:
λ3 =
Результат занести в таблицу 2.
14. Вычислить среднее значение длины световой волны:
<λ> =
15. Найти отклонения λ i от среднего:
Δλ1 = Δλ2 =
Δλ3 =
16. Найти среднюю квадратичную погрешность:
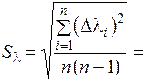
17. Задать надежность α (0,9 или 0,95) и в таблице найти коэффициент Стьюдента
tα = при α =
18. Найти абсолютную погрешность определения длины волны:
∆λ = tα·Sλ =
19. Найти относительную погрешность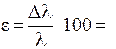
Результаты занести в таблицу 2.
Выводы
В первой части работы моделировали явление ………………………….………
…………………………….., наблюдаемое при прохождении ………………………… ……………………..………………………………… через непрозрачный экран с ………………………………….
По наблюдаемой ………………………………… картине при заданном значении ………………………………………………………………………. измерили …………
………………………………………………………………………………………………..
……………………………………………………………………………………………….
По полученным данным рассчитали длину волны:
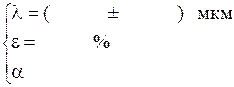
Экспериментальное значение длины волны (соответствует или не соответствует – почему – высказать предположение)
………………………………… теоретическому значению …………………………….
…………………………………………………………….…………………………………
|
|
|
…………………………………………………………….…………………………………
…………………………………………………………….…………………………………
Во второй части работы моделировали прохождение световой волны через дифракционную решетку, имеющую …… щелей, наблюдали …………………………… …………………………………………..и измерили ………………………………………
…………………………………………………………….…………………………………
…………………………………………………………….…………………………………
…………………………………………………………….…………………………………
По полученным данным рассчитали длину волны:
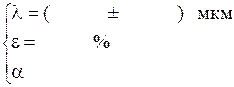
Экспериментальное значение длины волны (соответствует или не соответствует – почему – высказать предположение)
………………………………… теоретическому значению …………………………….
…………………………………………………………….…………………………………
…………………………………………………………….…………………………………
…………………………………………………………….…………………………………
|
|
|
