 |
Определение предикатов на основе правил
|
|
|
|
Рассмотренный ранее пример программ можно легко дополнить с применением многих интересных способов. Вначале введем информацию о мужском или женском поле людей, участвующих в предикате parent. Эту задачу можно решить, добавив следующие факты к программе:
female(pam).
male(tom).
male(bob).
female (liz).
female(pat).
female(ann}.
male(jim).
В этом случае введены предикаты male и female. Эти предикаты являются унарными (или одноместными). Бинарные предикаты типа parent определяют связь между парами объектов. С другой стороны, унарные отношения могут использоваться для объявления простых свойств объектов, которые они могут иметь или не иметь. Первое из приведенных выше унарных предложений можно прочитать таким образом: Пэм — женщина. Вместо этого информацию, объявленную в двух унарных отношениях, можно передать с помощью одного бинарного отношения. В таком случае приведенная выше часть программы примет примерно такой вид:
sех(pam, feminine).
sex(tom, masculine).
sex(bob, masculine).
В качестве следующего дополнения к программе введем предикат offspring (отпрыск), обратный предикату parent. Предикат offspring можно определить таким же образом, как и parent, предоставив список обычных фактов о предикате offspring, и в качестве каждого факта указать такую пару людей, что один из них является сыном или дочерью другого, например:
вffspring(liz, tom).
Но предикат offspring можно определить гораздо более изящно, используя то, что он является противоположным parent и что parent уже было определено. Этот альтернативный способ может быть основан на следующем логическом утверждении:
Для всех X и Y Y является сыном или дочерью X, если X является родителем Y.
Такая формулировка уже более близка к синтаксису языка Prolog. Соответствующее предложение Prolog, которое имеет тот же смысл, выглядит таким образом:
|
|
|
offspring(Y, X):- parent(X, Y).
Это предложение можно также прочитать так:
Для всех X и Y, если X является родителем Y, то Y является сыном или дочерью X.
Предложения Prolog, такие как ospring(Y, X):- parent(X, Y). называются правилами. Между фактами и правилами существует важное различие. Такие факты, как parent(tom, liz), представляют собой логические утверждения, которые всегда и безусловно являются истинными. С другой стороны, правила представляют собой утверждения, которые становятся истинными, если удовлетворяются некоторые условия. Поэтому принято считать, что правила состоят из следующих частей:
• условие (правая часть правила);
• заключение (левая часть правила).
Если условие parernt(X, Y) является истинным, то его логическим следствием становится offspring(Y, X).
Применение правил в языке Prolog иллюстрируется в следующем примере. Зададим программе вопрос, является ли Лиз дочерью Тома:
?- offspring(liz, tom).
Поскольку в программе отсутствуют факты о дочерях и сыновьях, единственным способом поиска ответа на этот вопрос является использование правила с определением предиката offspring. Данное правило является общим в том смысле, что оно применимо к любым объектам X и Y; но его можно также применить и к таким конкретным объектам, как liz и tom. Чтобы применить правило к объектам liz и tom, вместо Y необходимо подставить liz, а вместо X — tom. Это действие называется конкретизацией переменных (в данном случае — X и Y), которое выполняется следующим образом:
X = tom и Y = liz
После конкретизации будет получен частный случай общего правила, который выглядит следующим образом:
offspring(liz, tom):- parent(tom, liz).
Часть с обозначением условия принимает вид parent(tom, liz).
После этого система Prolog пытается определить, является ли истинной часть с обозначением условия. Поэтому первоначальная цель:
offspring(liz, tom) заменяется подцелью parent(tom, liz)
|
|
|
Оказалось, что задача достижения новой цели является тривиальной, поскольку ее можно найти как факт в рассматриваемой программе. Это означает, что часть данного правила с обозначением заключения также является истинной, и Prolog в качестве ответа на вопрос выводит yes.
Теперь введем в рассматриваемый пример программы еще некоторую информацию о семейных отношениях. Определение отношения mother может быть основано на следующем логическом утверждении:
Для всех X и Y, X является матерью Y, если X является одним из родителей Y и X - женщина.
Это утверждение можно перевести на язык Prolog в виде следующего правила:
mother(X, Y):- parent(X, Y), female(X).
Запятая между двумя условиями указывает на конъюнкцию этих условий; это означает, что оба условия должны быть истинными.
Предикат grandparent (родитель родителя) можно непосредственно записать на языке Prolog следующим образом:
grandparent(X, Z):- parent(X, Y), parent(Y, Z).
Схема предиката sister имеет следующее определение:
Для любого X и Y X является сестрой Y, если
1) X и Y имеют общего родителя и
2) X - женщина.
На язык Prolog этот предикат описывется следующим образом:
sister(X, Y):- parent(Z, X), parent(Z, Y), female(X).
Теперь системе можно задать вопрос:
?- sister(ann, pat).
Ответом должно быть "yes", как и следовало ожидать. Поэтому можно сделать вывод, что предикат sister в том виде, в каком он определен, действует правильно. Но в рассматриваемой программе имеется незаметный на первый взгляд недостаток, который обнаруживается при получении ответа на вопрос о том, кто является сестрой Пэт:
?- sister(X, pat).
Prolog находит два ответа, и один из них может оказаться неожиданным.
X = ann;
X = pat
Итак, Пэт является сестрой самой себя?! По-видимому, такой исход не подразумевался при определении предиката sister. Но согласно правилу, касающемуся сестер, ответ системы Prolog является полностью обоснованным. В правиле о сестрах нет упоминания о том, что X и Y не должны быть одинаковыми, если X рассматривается как сестра Y. Поскольку это требование не предъявляется, система Prolog предполагает, что X и Y могут быть одинаковыми, и поэтому приходит к заключению, что любая женщина, имеющая родителя, является сестрой самой себя.
Чтобы исправить приведенное выше правило о сестрах, необходимо дополнительно указать, что X и Y должны быть разными. Такую задачу можно решить несколькими способами, но на данный момент предположим, что системе Prolog уже известно отношение different и условие different(X, Y) удовлетворяется, если и только если X и Y не равны. Поэтому усовершенствованное правило для отношения sister может выглядеть следующим образом:
|
|
|
Sister(X, Y):-parent(Z, X),parent(Z, Y),female(X),different(X, Y).
На основании изложенного в этом разделе можно сделать следующие важные выводы.
• Программы Prolog можно дополнять, вводя новые предложения.
• Предложения Prolog относятся к трем типам: факты, правила и запросы.
• С помощью фактов можно вводить в программу сведения, которые всегда и безусловно являются истинными.
• С помощью правил можно вводить в программу сведения, которые являются истинными в зависимости от заданного условия,
• В процессе вычисления переменные можно заменять другими объектами.
В таком случае переменная становится конкретизированной.
Рекурсивные правила
Введем еще один предикат в рассматриваемую программу с описанием семьи —предикат predecessor (предок). Этот предикат будет определен через предикат parent. Его можно представить с помощью двух правил. Первое правило определяет прямых (непосредственных) предков, а второе правило — непрямых предков. Говорят, что некоторый X является непрямым предком некоторого Z, если существует цепочка родительских связей между людьми от X до Z. В приведенном примере Том является прямым предком Лиз и непрямым предком Пэт.
Первое правило является простым и может быть сформулировано следующим образом:
Для всех X и Z, X - предок Z, если X - родитель Z.
Это утверждение можно сразу же перевести на язык Prolog таким образом:
predecessor(X, Z):-parent(X, Z).
Второе правил является более сложным, поскольку решение задачи представления цепочки родительских связей может вызвать некоторые проблемы. Предикат predecessor должен быть определен как множество следующих предложений:
predecessor(X., Z):-parent(X,Z).
predecessor(X, Z):-parent(X, Y),parent(Y, Z).
predecessor(X, Z):-parent(X, Y1),parent(Yl, Y2),parent(Y2, Z).
predecessor(X,Z):-parent(X,Yl),parent(Yl,Y2),parent(Y2,Y3),parent(Y3, Z).
Пределы действия этой программы довольно ограничены. Она позволяет находить предков в генеалогическом дереве только до определенного уровня, поскольку длина цепочки людей между предками и потомками лимитируется длиной существующих предложений с определением предков.
|
|
|
Но для формулировки отношения predecessor можно применить гораздо более изящную и правильную конструкцию. Она является правильной в том смысле, что позволяет находить предков до любого колена. Основная идея состоит в том, что предикат predecessor должен быть определен в терминах себя самого. Эта идея выражается в виде следующего логического утверждения:
Для всех Х и Z X - предок Y, если имеется такой Y, что
1) X — родитель Y и
2) Y - предок Z.
Предложение Prolog1, имеющее такой же смысл, приведено ниже.
predecessor(X, Z):-parent(X, Y),predecessor(Y, Z}.
Таким образом, сформулирована полная программа для отношения predecessor, которая состоит из двух правил: первое из них определяет прямых, а вторая — непрямых предков. Оба правила, записанные вместе, приведены ниже.
predecessor(X, Z):-parent(X, Z).
predecessor(X, Z):-parent(X,Y),predecessor(Y, Z).
Ключом к анализу этой формулировки является то, что отношение predecessor используется для определения самого себя. Подобные определения имеют общее название рекурсивных.
Cистема Prolog действительно способна очень легко применять рекурсивные определения. Рекурсивное программирование фактически является одним из фундаментальных принципов программирования на языке Prolog. Без использования рекурсии на языке Prolog невозможно решать какие-либо сложные задачи.
Возвращаясь к рассматриваемой программе, можно задать системе Prolog вопрос о том, кто является потомками Пэм. Иными словами, для кого Пэм является предком?
? - predecessor(pam, X).
X = bob;
X = ann;
X = pat;
X = jim
Ответы системы Prolog, безусловно, верны и логически следуют из определения отношений predecessor и parent.
Семантическая сеть
В семантической структуре понятий существуют отношения, по крайней мере, двух типов:
отношение включения (IS — A);
отношение «целое – часть» (PART — OF).
Например, в предложении
человек IS — A млекопитающее
основной мыслью является, что человек принадлежит к классу млекопитающих. Это означает, что имеет место отношение включения. Для этих отношений характерным является то, что экземпляры понятий нижнего уровня содержат все атрибуты понятий верхнего уровня. Это свойство называется наследованием атрибутов между уровнями иерархии IS — A.
Отношение «целое - часть» можно иллюстрировать предложением
нос PART — OF тело,
которое характеризует то, что экземпляры понятия «нос» являются частью любого экземпляра понятия «тело».
|
|
|
Часто используется графическое представление семантических сетей в виде диаграммы. Так, предложение
все собаки – млекопитающие
можно представить графом, содержащим две вершины, соответствующие понятиям, и дугу, указывающую отношение между ними (рис. 3.2).

Рис. 3.2
Если собака имеет конкретное имя, например, Шарик, то семантическая сеть может быть расширена (рис. 3.3).

Рис. 3.3
Наряду с тем, что с помощью данной сети описаны два факта
Шарик – собака
собака – млекопитающее
из нее можно вынести, используя отношение наследования, факт
Шарик – млекопитающее.
Этот факт показывает, что способ представления семантической сетью позволяет легко делать выводы благодаря иерархии наследования.
Семантическими сетями можно представлять знания, касающиеся атрибутов объекта. Например, факт
Собаки имеют лапы
можно отобразить в виде рисунка 3.4.
Это означает, что, используя отношения «IS – A» и «PART – OF», можно вывести факт:
Шарик имеет лапы.
Вершины в семантической сети обычно показывают объект проблемной области или ситуацию, а дуги — это отношения между ними. При расширении семантической сети в ней возникают дополнительные отношения. Например, если рассматриваемую сеть дополнить фактами
Шарик имеет конуру
и Шарик имеет конуру с весны по осень,

Рис. 3.4
то получим еще одну семантическую сеть (рис. 3.5).
Если подробнее рассмотреть структуру, то семантическая сеть представляет собой ориентированный граф с помеченными (поименованными) дугами и вершинами. При этом вершинам семантической сети соответствуют понятия, события и свойства (рис. 3.6).

Рис. 3.5
Понятия представляют собой сведения об абстрактных или физических объектах предметной области (реального мира).
События представляют собой действия, происходящие в реальном мире, и определяются указанием: типа действия; ролей, которые играют объекты в этом действии.
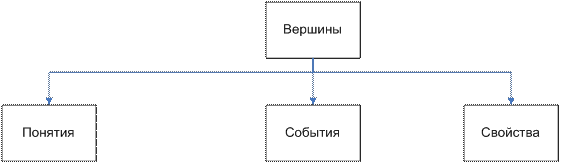
Рис. 3.6
Свойства используются для уточнения понятий и событий. Применительно к понятиям они описывают их особенности и характеристики (цвет, размер, качество), а применительно к событиям — продолжительность, время, место.
Дуги графа семантической сети отображают многообразие семантических отношений, которые условно можно разделить на четыре класса (рис. 3.7).

Рис. 3.7
Лингвистические отношения отображают смысловую взаимосвязь между событиями, между событиями и понятиями или свойствами. Лингвистические отношения бывают:
глагольные (время, вид, род, залог, наклонение);
атрибутивные (цвет, размер, форма);
падежные (см. ниже).
Логические отношения — это операции, используемые в исчислении высказываний: дизъюнкция, конъюнкция, импликация.
Теоретико - множественные — это отношения подмножества, отношение части целого, отношение множества и элемента. Примерами таких отношений являются IS—A, PART—OF.
Квантифицированные отношения — это логические кванторы общности и существования. Они используются для представления таких знаний, как «Любой станок надо ремонтировать», «Существует работник А, обслуживающий склад Б».
Рассмотрим использование семантических сетей для представления структуры понятий. Основой для определения любого понятия является множество его отношений с другими понятиями. Обязательными отношениями являются:
класс, которому принадлежит данное понятие;
свойства, выделяющие понятие из всех понятий данного класса;
экземпляры данного понятия.
Так как термы, используемые в определении понятия, сами являются понятиями, то их определение организуется по той же схеме. В итоге связи понятий образуется сетевая структура, в которой используется как минимум два типа связей (IS — A и PART – OF).
Пример: Семантическая сеть, отображающая связи понятий при описании знаний о структуре понятия «Юридическое лицо» будет иметь вид, представленный на рисунке 3.8.

Рис. 3.8
Так, для понятия «предприятие» в этой сети:
определен класс, которому оно принадлежит, и все свойства которого оно наследует (юридическое лицо);
выделено три свойства, которые выделяют это понятие из всех остальных понятий класса «Юридическое лицо»;
определен экземпляр данного понятия, а именно: Авиазавод.
Рассмотрим использование семантических сетей для представления структуры событий.
При представлении событий предварительно выделяются простые отношения, которые характеризуют основные компоненты события. В первую очередь из события выделяется действие, которые обычно описываются глаголом. Далее определяются объекты:
1. которые действуют;
2. над которыми эти действия выполняются.
Все связи понятий, событий и свойств с действием (глаголом) называют падежами или падежными отношениями, которые относятся к классу лингвистических отношений. Обычно рассматривают следующие основные падежи:
| Падеж | Лингвистическое отношение, определяющее связь действия с: |
| агент | предметом, являющимся инициатором действия; |
| объект | предметом, подвергающимся действию; |
| источник | размещение предмета перед действием; |
| приемник | размещение предмета после действия; |
| время | моментом выполнения действия; |
| место | местом проведения действия; |
| цель | действием другого события. |
Так, например, семантическая структура знания о событии «Директор авиазавода остановил 30.03.08 цех 4, чтобы заменить оборудование» представлена на риунке 3.9.

Рис. 3.9
Особенность семантической сети как модели знаний состоит в единстве базы знаний и механизма вывода.
Основным способом вывода в семантической сети является сопоставление частей сетевой структуры. Сущность его состоит в следующем. Содержание и цель запроса списывается автономной семантической сетью (сетью запроса), построенной по тем же правилам и отображающей те же объекты и отношения, которые представлены семантической сетью. Поиск ответа на запрос реализуется сопоставлением сети запроса с фрагментами семантической сети. Положительный результат сопоставления позволяет получить один из ответов запроса. Все ответы можно получить путем обнаружения всех сопоставимых с сетью запроса фрагментов
Рассмотрим пример семантической сети, отражающей подчиненность сотрудников организации (рис. 3.10).

Рис. 3.10
Запрос: «Кто руководит Сидоровым?» представим в виде подсети (рис. 3.11).

Рис. 3.11
Сопоставление общей сети с сетью запроса начинается с поиска вершины «руководит», имеющий ветвь «объект», направленную к вершине «Сидоров». Затем производится переход по ветви «агент», что и приводит к ответу «Петров».
Необходимо отметить ряд преимуществ семантической сети:
1) описание понятий и событий производится на уровне, очень близком к естественному языку;
2) обеспечивается возможность объединения различных фрагментов сети;
3) отношение между понятиями и событиями образуют достаточно небольшое и хорошо формализованное множество;
4) для каждой операции над данными и знаниями можно выделить из полной сети, представляющей все знания, некоторый ее участок, который охватывает необходимые в данном запросе смысловые характеристики.
Фреймовая модель
В сложных семантических сетях, включающих множество понятий, процесс обновления узлов и контроль связей между ними становится затруднительным. При этом количество опосредованных связей между понятиями резко возрастает.
Термин фрейм (от англ. frame – рамка, каркас) предложен Марвином Минским, одним из пионеров ИИ, в 70-е годы ХХ века для обозначения структуры знаний для восприятия пространственных сцен. Эта модель, как и семантическая сеть, имеет глубокое психологическое обоснование.
Фрейм – это абстрактный образ для представления некоего стереотипа восприятия.
Отправным моментом для данной теории служит тот факт, что человек, пытаясь познать новую для себя ситуацию или по-новому взглянуть на уже привычные вещи, выбирает из своей памяти некоторую структуру данных (образ), называемую нами фреймом, с таким расчетом, чтобы путем изменения в ней отдельных деталей сделать ее пригодной для понимания более широкого класса явлений или процессов.
Фрейм является структурой данных для представления стереотипной ситуации. С каждым фреймом ассоциирована информация разных видов. Одна ее часть указывает, каким образом следует использовать данный фрейм, другая - что предположительно может повлечь за собой его выполнение, третья - что следует предпринять, если эти ожидания не подтвердятся.
Фрейм можно представлять себе в виде сети, состоящей из узлов и связей между ними. "Верхние уровни" фрейма четко определены, поскольку образованы такими понятиями, которые всегда справедливы по отношению к предполагаемой ситуации. На более низких уровнях имеется много особых вершин-терминалов или "ячеек", которые должны быть заполнены характерными примерами или данными.
Марвин Минский «Фреймы для представления знаний»
Фреймы подразделяются на:
· Фреймы – образцы или прототипы, хранящиеся в базе знаний
· Фреймы-экземпляры, которые создаются для отображения реальных фактических ситуаций на основе поступающих данных
· Модель фрейма является достаточно универсальной, поскольку позволяет отобразить все многообразие знаний о мире через:
фреймы-структуры, использующиеся для обозначения объектов и понятий (заем, залог, вексель);
· фреймы-роли (менеджер, кассир, клиент);
· фреймы-сценарии (банкротство, собрание, празднование именин);
фреймы-ситуации (тревога, авария, рабочий режим устройства).
Во фреймовых моделях фиксируется жесткая структура информационных единиц, которая называется фреймом-прототипом (протофреймом). В общем виде она выглядит следующим образом:
(Имя фрейма:
Имя слота 1 (значение слота 1);
Имя слота 2 (значение слота 2);
...
Имя слота К (значение слота К)
)
Фрейм-прототип - фрейм, в котором значения слотов не определены
Ту же запись можно представить в виде таблицы, дополнив ее двумя столбцами.
| ИМЯ СЛОТА | ЗНАЧЕНИЕ СЛОТА | СПОСОБ ПОЛУЧЕНИЯ ЗНАЧЕНИЯ | ПРИСОЕДИ-НЕННАЯ ПРОЦЕДУРА |
Дополнительные столбцы предназначены для описания способа получения слотом его значения и возможного присоединения к тому или иному слоту специальных процедур, что допускается в теории фреймов.
При конкретизации фрейма ему и слотам присваивают конкретные имена и происходит заполнение слотов.
Из фреймов-прототипов получаются фреймы-экземпляры. Экземпляр фрейма - фрейм, в котором определены значения слотов.
Значением слота может быть:
· числа или математические соотношения,
· тексты на естественном языке,
· программы,
· правила вывода,
· ссылки на другие слоты данного фрейма или других фреймов,
· набор слотов более низкого уровня – реализация принципа «матрешки».
Если в качестве значения слота выступает имя другого фрейма, то образуются сети фреймов.
ПРИМЕР
Фрейм-прототип:
(Список студентов:
Фамилия (значение слота 1);
Год рождения (значение слота 2);
Специальность (значение слота 3);
Средний балл (значение слота 4)
)
Фрейм-экземпляр:
(Список студентов:
Фамилия (Иванов-Петров-Сидоров)
Год рождения (1980-1981-1982)
Специальность (ОЗИ-САПР-ПО)
Средний балл (4-4-5)
)
Связи между фреймами могут задаваться значениями специального слота с именем «Связь».
Важнейшее свойство теории фреймов – заимствование из теории семантических сетей наследования свойств. И во фреймах и в семантических сетях наследование происходит по AKO-связям (A-Kind-Of = это).
Слот AKO указывает на фрейм более высокого уровня иерархии, откуда неявно наследуются, то есть переносятся, значения аналогичных слотов.
ПРИМЕР
В сети фреймов понятие «ученик» наследует свойства фреймов «ребенок» и «человек», которые находятся на более высоком уровне иерархии.
На вопрос «любят ли ученики сладкое» следует ответ «да», так как этим свойством обладают все дети, что указано во фрейме «ребенок». Наследование свойств может быть частичным, так как возраст учеников не наследуется из фрейма «ребенок», поскольку указан явно в своем собственном фрейме.

Основное преимущество фреймов как модели представления знаний – эта модель отражает концептуальную основу организации памяти человека, а также ее гибкость и наглядность.
|
|
|


