Математическая постановка задачи моделирования потребительского спроса.

Лабораторная работа № 3.

МОДЕЛИРОВАНИЕ ПОТРЕБИТЕЛЬСКОГО СПРОСА

 

Будем считать, что потребитель располагает доходом M, который он полностью тратит на потребление благ (продуктов). Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определенное количество благ. Математическая модель такого его поведения называется моделью потребительского выбора.

Рассмотрим потребительские наборы из двух благ - вектор (x₁,x₂), координата x₁ которого равна количеству единиц первого блага, а координата x₂ равна количеству единиц второго блага. Такая модель удобна, прежде всего, возможностью графической интерпретации, сохраняя при этом все принципиальные свойства общей модели.

Выбор потребителя (индивидуума) характеризуется отношением предпочтения, суть которого состоит в следующем. Ha множестве потребительских наборов (x₁,x₂) определенна функция u(x₁,x₂) (называемая функцией полезности потребителя), значение u(x₁,x₂) которой при потребительском наборе (x₁,x₂) равно потребительской оценке индивидуума для этого набора. Потребительскую оценку u(x₁,x₂) набора (x₁,x₂) принято называть уровнем (или степенью) удовлетворения потребностей индивидуума, если он приобретает или потребляет данный набор (x₁,x₂). Каждый потребитель имеет, вообще говоря, свою функцию полезности.

Функция полезности удовлетворяет следующим свойствам:

1) , .

Первые частные производные называются предельными полезностями соответствующего блага.

2) .

Отражают закон убывания предельной полезности.

Линия, соединяющая потребительские наборы (x₁,x₂), имеющие один и тот же уровень удовлетворения потребностей индивидуума, называется линией безразличия. Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличий называется картой линий безразличия. На рис. 1 показан фрагмент карты линий безразличия. Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются. Если линия безразличия l _t3 расположена выше. и правее ("северо-восточнее") линии безразличия то t₃>t₂. Верно и обратное. Иными словами, чем "северо-восточнее" расположена линия безразличия, тем большему уровню удовлетворения потребности она соответствует.

 

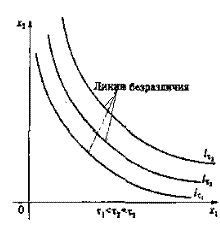
Рис. 1. Карта линий безразличий

 

Задачи потребительского выбора (Задачарационального поведения потребителя на рынке) заключается в выборе такого потребительского набора (x₁⁰,x₂⁰), который максимизирует его функцию полезности при заданном бюджетном ограничении.

Бюджетное ограничение означает, что денежные расходы на продукты не могут превышать дохода, т.е. p₁x₁+p₂x₂ M, где p₁ и p₂ – рыночные цены одной единицы первого и второго продуктов соответственно, а – доход индивидуума, который он готов потратить на приобретение первого и второго продуктов. Величины p₁, p₂, и I заданы.

 

Математическая постановка задачи моделирования потребительского спроса.

1.1. Задача максимизации функции полезности при заданном бюджетном ограничении.

Формально задача потребительского выбора имеет вид:

 

u(x₁, x₂) 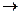(max) (1)

при условиях

p₁x₁+p₂x₂£ M

x₁³0, x₂³0.

 

Допустимое множество (т.е. множество наборов благ, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности. Поиск этой точки можно интерпретировать графически как последовательный переход на линии все более высокого уровня полезности (вправо – вверх) до тех пор, пока эти линии еще имеют общие точки с допустимым множеством.

Набор (x , x ), который является решением задачи потребительского выбора, принято называть оптимальным для потребителя или локальным рыночным равновесием потребителя.

Остановимся на свойствах задачи. Во-первых, решение задачи (x , x ) сохраняется при любом монотонном (т.е. сохраняющем порядок значений) преобразовании функции полезности u(x₁, x₂). Поскольку значение u(x , x ) было максимальным на всем допустимом множестве, оно остается таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остается неизменным).

Во-вторых, решение задачи потребительского выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и тоже число раз l.

Это равнозначно умножению на положительное число l обеих частей бюджетного ограничения p₁x₁+p₂x₂£ М, что дает неравенство, эквивалентное исходному. Поскольку ни цены, ни доход M не входят в функцию полезности, задача остается той же, что и первоначально.

В приведенной постановке задача потребительского выбора является задачей нелинейного программирования. Однако если на каком-то потребительском наборе (x₁, x₂), бюджетное ограничение p₁x₁+p₂x₂£ M будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого-либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор (x , x ), максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. p₁x +p₂ x = M. Графически это означает, что решение (x , x ) задачи потребительского выбора должно лежать на бюджетной прямой, которую удобнее всего провести через точки пересечения с осями координат и .

Итак, задачу потребительского выбора можно заменить задачей на условный экстремум функции u(x₁, x₂)

 

u(x₁, x₂) 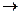(max) (2)

при условии

p₁x₁+p₂x₂ = M.

 

Для решения этой задачи на условный экстремум применим метод Лагранжа.

Выписываем функцию Лагранжа

, (3)

Находим ее первые частные производные по переменным x₁, x₂ и l приравниваем эти частные производные к нулю:

 

,

, (4)

.

 

Исключив из полученной системы трех уравнений с тремя неизвестными неизвестную l, получим систему двух уравнений с двумя неизвестными x₁ и x₂

 

, (5)

p₁x₁+p₂x₂ = M.

Решение (x , x ) этой системы есть “укороченная” критическая точка функции Лагранжа. В [1] доказано, что “укороченная” критическая точка
(x , x ) функции Лагранжа обязательно есть решение задачи потребительского выбора. Подставив решение (x , x ) в левую часть равенства

 

(6)

получим, что в точке (x , x ) локального рыночного равновесия индивидуума отношение предельных полезностей и продуктов равно отношению рыночных цен p₁ и p₂ на эти продукты

 

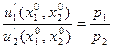. (7)

 

В связи с тем, что отношение равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия (x , x ), из (6) следует, что эта предельная норма равна отношению рыночных цен на продукты. Приведенный результат играет важную роль в экономической теории.

Геометрически решение (x , x ) можно итерпретировать как точку касания линии безразличия функции полезности с бюджетной прямой
p₁x₁+p₂x₂ = M (см. рис. 2).

 

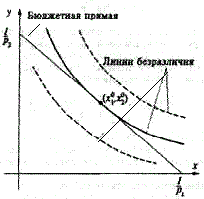
Рис. 2. Линии уровня

 

Координаты x и x решения (x , x ) задачи потребительского выбора есть функции параметров p₁, p₂ и M

 

,

.

Эти функции называются функциями потребительского спроса по Маршаллу.

В общем случае для набора состоящего из n благ, количество блага зависит от цен благ и бюджета индивида M:

, .

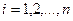Когда все факторы, определяющие объем спроса на благо, кроме его цены, постоянны, функция спроса принимает частный вид функции спроса по цене: . Объем спроса на благо при постоянных ценах в зависимости от дохода принимает частный вид функции спроса по доходу: .

Предположим, что функция полезности имеет вид

,

где , а также – некоторые постоянные величины. При этом показатели степени 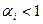, 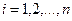. Это условие гарантирует, что предельные полезности являются убывающими функциями.

Так как , то

.

 

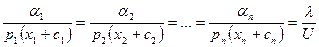Отсюда

и

,

откуда

.

Тогда функция спроса на -е благо выражается соотношением

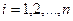, . (8)

В частном случае, когда , функция полезности имеет вид

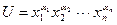, (8.1)

и для функции спроса на -е благо справедлива следующая зависимость от цены на -е благо и величины дохода:

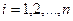, . (8.2)

 

1.2 Задача минимизации расходов при фиксированном уровне полезности.

 

Пусть задан определенный уровень полезности , который устраивает потребителя.Требуется определить набор благ, позволяющий выйти на этот уровень с наименьшими расходами. Аналитически задача минимизации расхода потребителя формулируется следующим образом

 

p₁x₁+p₂x₂ = M(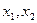) 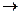min (9)

u(x₁, x₂)= (10)

 

Решим задачу минимизации методом Лагранжа.

 

(11)

Решив полученную систему трех уравнений с тремя неизвестными, найдем значения , , 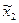, которые зависят от значений . Функции

) (12)

)

называют функциями спроса по Хиксу (функциями компенсированного спроса).Подставляя функции спроса по Хиксу в целевую функцию p₁x₁+p₂x₂ = M(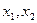) получим функцию,которая называется функцией минимального расхода.

 

(13)

 

Задания к лабораторной работе:

Задание №1

Функция полезности,имеет вид 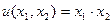, бюджетное ограничение

p₁x₁+p₂x₂ = M. (14)

Исходные данные для различных вариантов приведены в таблице 1

 

M

Таблица 1

 

а) Найдите функции спроса по Маршаллу

,

для заданной функции полезности.

б) Найдите оптимальный набор благ для заданного бюджетного ограничения, т.е. значения и .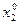

в) Найдите уровень полезности U, соответствующий найденному оптимальному набору благ 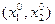. Постройте в одной системе координат изокванту (кривую безразличия) функции полезности

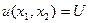и бюджетную линию (14). Объясните их взаимное положение.

г) Найдите функцию спроса по цене

, зафиксировав доход и цену второго товара на уровне заданном в варианте. Постройте графики полученных функций.

Найдите функции спроса по доходу , зафиксировав цены и в соответствии с вариантом. Постройте их графики.

 

Задание №2

Используем функцию полезности и исходные данных из задания № 1. Пусть цена первого блага увеличилась на 80% и стала равна 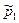при неизменном доходе M и цене второго блага .

а) Найдите оптимальный набор благ и , соответствующий новому уровню цен. Определите уровень полезности , соответствующий найденному оптимальному набору благ.

б) Постройте в одной системе координат изокванту (кривую безразличия) функции полезности

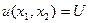и новую бюджетную линию , а также изокванту и старую бюджетную линию p₁x₁+p₂x₂ = M. Объясните расположение линий.

в) Чтобы сохранить прежний уровень полезности при возросшей цене блага потребитель должен получить компенсирующую надбавку к своему доходу.Определите каким должен стать доход потребителя , чтобы при новом уровне цен сохранился прежний уровень полезности . Определите потребительский спрос , решив систему уравнений

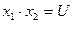
г) Исследуйте изменение потребительского спроса в случае если доход потребителя возрастет до величины ,при этом цены благ останутся на прежнем уровне 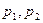. Найдите оптимальный набор благ и уровень полезности для этого случая

г) Постройте в одной системе координат:

1) изокванту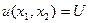

2) бюджетную линию p₁x₁+p₂x₂ = M

3) бюджетную линию

4)изокванту

5) бюджетную линию

6) изокванту

7) бюджетную линию p₁x₁+p₂x₂ =

Объясните расположение линий и взаимосвязь значений наборов благ 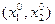, и с точки зрения уравнения Слуцкого.

Задание №3

Функция полезности,имеет вид 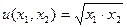. Уровень полезности , который устраивает потребителя, и цены благ по вариантам заданы в таблице 2

	6.124	3.873	4.33	4.743	3.873	3.75	5.303	6.124	5.303

Таблица 2

а) Найдите методом Лагранжа по формулам (11) потребительский набор , минимизирующий функцию расходов потребителя (9). Найдите функции спроса по Хиксу (12).

б) Найдите минимальный расход , соответствующий потребительскому набору , по формуле (9). Постройте в одной системе координат изокванту (кривую безразличия) функции полезности

и бюджетную линию p₁x₁+p₂x₂ = .

в) Напишите уравнение функции минимального расхода (13) и постройте график зависимости минимального расхода от цены , зафиксировав значение и в соответствии со своим вариантом. Аналогично постройте график зависимости минимального расхода от цены .

Поделиться:

Воспользуйтесь поиском по сайту: