 |
в системе электроснабжения
|
|
|
|
Симметричная трехфазная система напряжений может быть представлена тремя выражениями:
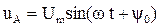 ; (3.25)
; (3.25)
 ; (3.26)
; (3.26)
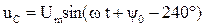 , (3.27)
, (3.27)
где y0 – начальная фаза напряжения uA.
При симметричной трехфазной системе
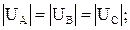 (3.28)
(3.28)
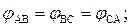 (3.29)
(3.29)
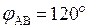 .
.
Если значения напряжения фаз оказываются различными или углы между фазами не равны 120°, то симметричная система преобразуется в несиммет-ричную.
Для удобства расчетов несимметричная трехфазная система векторов (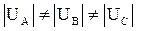 или
или 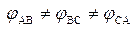 , или оба фактора вместе) разлагается на симметричные составляющие:
, или оба фактора вместе) разлагается на симметричные составляющие:
прямой последовательности –
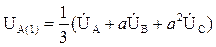 ; (3.30)
; (3.30)
обратной –
 ; (3.31)
; (3.31)
нулевой –
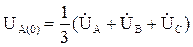 . (3.32)
. (3.32)
Напомним, что оператор
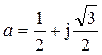 и
и 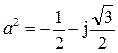 . (3.33)
. (3.33)
Для симметричных систем напряжений прямой и обратной последовательностей можно записать:
прямая последовательность –
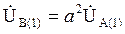 ; (3.34)
; (3.34)
 ; (3.35)
; (3.35)
обратная –
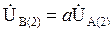 ; (3.36)
; (3.36)
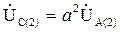 ; (3.37)
; (3.37)
нулевая –
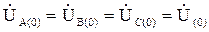 . (3.38)
. (3.38)
Используя такой метод, можно считать, что симметричные составляющие разных фаз не зависят друг от друга.
Количественно несимметрия токов и напряжений оценивается величиной коэффициента несимметрии:
тока –
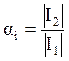 ; (3.39)
; (3.39)
напряжений по обратной последовательности –
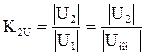 , (3.40)
, (3.40)
напряжений по нулевой последовательности –
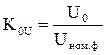 , (3.41)
, (3.41)
где I2, I1 – токи обратной и прямой последовательностей соответственно;
U2, U1, U0 – напряжение обратной, прямой и нулевой последовательности;
Uном ф – номинальное фазное напряжение.
Несимметрия токов приводит
к недоиспользованию мощностей генераторов, трансформаторов и про-пускной способности линии, так как в любой фазе нагрузка не может превышать номинального значения;
возрастанию потерь в системе электроснабжения из-за неравномерности нагрузки фаз;
|
|
|
возникновению несимметрии напряжения в узлах сети;
дополнительному уменьшению располагаемой мощности генераторов электрических станций из-за повышенного нагрева ротора и обмоток возбуждения.
Запишем мгновенные значения:
электрической мощности –
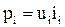 ; (3.42)
; (3.42)
напряжения –
 ; (3.43)
; (3.43)
тока –
 . (3.44)
. (3.44)
Следовательно,
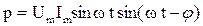 . (3.45)
. (3.45)
Известно, что 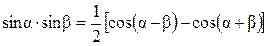 . Учтем, что
. Учтем, что 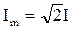 ;
; 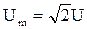 , где I, U – действующие (среднеквадратичные) значения тока и напряжения за период соответственно.
, где I, U – действующие (среднеквадратичные) значения тока и напряжения за период соответственно.
Тогда
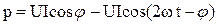 ; (3.46)
; (3.46)
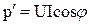 – (3.47)
– (3.47)
активная мощность, не зависящая от времени;
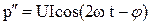 – (3.48)
– (3.48)
колеблющаяся мощность.
Отношение
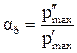 – (3.49)
– (3.49)
коэффициент неравномерности мощности;
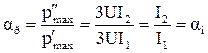 , (3.50)
, (3.50)
где ai – коэффициент несимметрии токов.
Таким образом, для трехфазной цепи коэффициент несимметрии токов численно равен коэффициенту неуравновешенности электрической мощности.
3.4.1. Несимметрия токов одной тяговой подстанции
Вспомним схему питания контактной сети от одной тяговой подстанции (рис. 3.7).
Мгновенное значение мощности в плече а
 (3.51)
(3.51)
Для плеча b
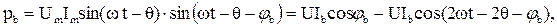 (3.52)
(3.52)
где q – угол между векторами напряжения плеч.
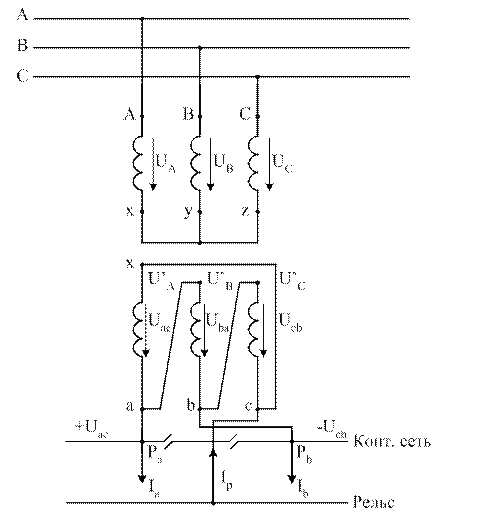
Рис. 3.7. Схема питания контактной сети от одной тяговой подстанции
Активная мощность
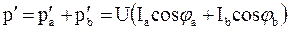 . (3.53)
. (3.53)
колеблющаяся –
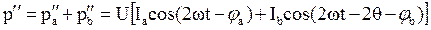 . (3.54)
. (3.54)
Обозначим 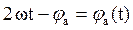 ;
;  . Тогда
. Тогда
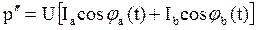 . (3.55)
. (3.55)
По правилу суммы проекций
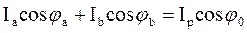 , (3.56)
, (3.56)
по теории косинусов
 .
.
Тогда
 . (3.57)
. (3.57)
Подставим выражение (3.57) в формулу (3.53).
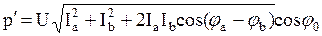 . (3.58)
. (3.58)
По аналогии для колеблющейся мощности
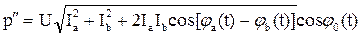 . (3.59)
. (3.59)
Подставляя значение 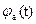 и
и 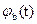 в выражение (3.59), получим:
в выражение (3.59), получим:
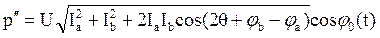 . (3.60)
. (3.60)
Максимальное значение активной мощности
 ; (3.61)
; (3.61)
колеблющейся –
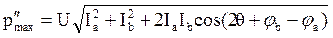 . (3.62)
. (3.62)
Тогда
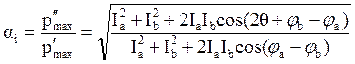 . (3.63)
. (3.63)
Пусть 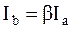 , где
, где 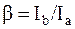 – отношение токов плеч, характеризует режим работы подстанции.
– отношение токов плеч, характеризует режим работы подстанции.
После замены отношения токов плеч  и подстановки ее в формулу (3.63) получим:
и подстановки ее в формулу (3.63) получим:
 . (3.64)
. (3.64)
Угол q между векторами напряжений плеч питания подстанции характеризует схему соединения обмоток трансформатора. Для трехфазного трансформатора, обмотки которого соединены по схеме Y/D, q = – 60°.
|
|
|
Углы 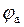 и
и 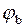 – фазы токов плеч относительно напряжений, отражают характер нагрузки. Обычно
– фазы токов плеч относительно напряжений, отражают характер нагрузки. Обычно 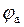 »
» 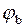 .
.
3.4.2. Несимметрия токов трехфазной системы,
питающей несколько однофазных нагрузок
Рассмотрим схему параллельной работы группы тяговых подстанций на контактную сеть (рис. 3.8).
Определим токи прямой и обратной последовательностей подстанций I, II, III типа. В общем виде для одного плеча мгновенная мощность может быть получена по формуле (3.42), а активная и колеблющаяся – по выражениям (3.47) и (3.48) соответственно.

|
Для трехфазной системы, питающей плечи тяговой нагрузки (когда система напряжений симметрична, а токи несимметричны и система нулевой последовательности отсутствует) можно записать, что
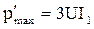 ; (3.65)
; (3.65) 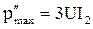 ; (3.66)
; (3.66)
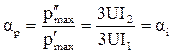 , (3.67)
, (3.67)
а также –
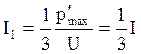 , (3.68)
, (3.68) 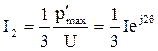 . (3.69)
. (3.69)
где I – ток плеча.
Для всех типов тяговых подстанций значения тока I1 приведены в табл. 3.1.
Таблица 3.1
Значения тока прямой последовательности при равномерной нагрузке
тяговых подстанций
| Тип подстанции | Плечо а | Плечо b | Для подстанции |
| I1 | I1 | ||
| I II III | 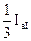
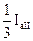
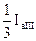
| 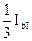
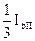
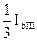
| 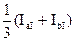
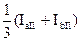
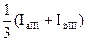
|
Значения тока обратной последовательности приведены в табл. 3.2. На основе данных табл. 3.2 построим векторную диаграмму (рис. 3.9).
Из диаграммы видно, что если нагрузки обратной последовательности и токи плеч одинаковы на всех подстанциях, то их векторы будут сдвинуты на 120°.
В общем случае положение векторов I2I, I2II, I2III зависит от соотношения токов плеч и они могут находиться в любой точке своей фазовой плотности.
Таблица 3.2
Значения тока обратной последовательности при равномерной нагрузке
тяговых подстанций
| Тип подстанции | Плечо а | Плечо b | Для подстанции | ||
| q | I1 | q | I1 | ||
| I II III | 0° 0° 120° | 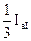
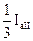
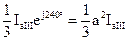
| 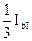
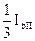
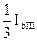
| 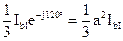
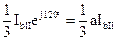
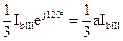
| 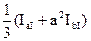
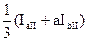

|
Несимметрия токов и напряжений в системе электроснабжения представлена на рис. 3.10. В результате чередования фаз токи обратной последовательности подстанций I, II, III сдвигаются по фазе.

Рис. 3.9. Фазовые плоскости токов
|
|
|
Благодаря этому на участках (0–1) и (1–2), где протекают токи нескольких подстанций, токи обратной последовательности существенно не увеличиваются (участок 1–2) или значительно снижаются (головной участок).
Для частного случая подстанций одинаковой мощности можно обеспечить полное симметрирование нагрузки на головном участке за счет 120-градусного сдвига.
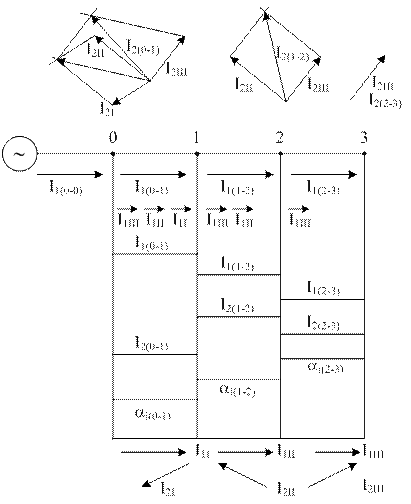
Рис. 3.10. Несимметрия токов в системе электроснабжения
3.4.3. Несимметрия напряжения в системах электроснабжения
Для рассмотрения несимметрии напряжений в системе электроснабжения обратимся к схеме, представленной на рис. 3.11, где показаны источник электрической энергии и точки присоединения тяговых подстанций 0, 1, 2, 3,..., К.
|
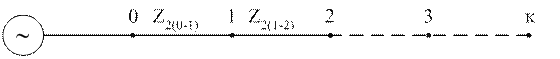
Рис. 3.11. Схема для рассмотрения напряжения
обратной последовательности в узлах
Напряжение обратной последовательности в узле К
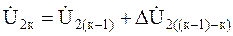 . (3.70)
. (3.70)
Потеря напряжения обратной последовательности до К-го узла определяется как
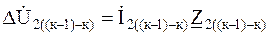 . (3.71)
. (3.71)
Например, для узла 2 можно записать:
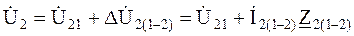 ; (3.72)
; (3.72)
Напряжение обратной последовательности в узле 1 можно получить следующим образом:
 , (3.73)
, (3.73)
где 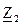 – сопротивление току обратной последовательности.
– сопротивление току обратной последовательности.
Библиографический список
1. Марквардт К. Г. Электроснабжение электрифицированных железных дорог/ К. Г. Марквардт. М.: Транспорт, 1982. 528 с.
2. Бурков А. Т. Электронная техника и преобразователи / А.Т. Бурков. М.: Транспорт, 1999. 464 с.
3. ГОСТ 13109-97. Нормы качества электрической энергии в системах электроснабжения общего назначения. Минск: Изд-во стандартов, 1998. 31с.
Учебное издание
МАСЛОВ Геннадий Петрович, МАГАЙ Герман Самсонович,
СИДОРОВ Олег Алексеевич
ё
ЭЛЕКТРОСНАБЖЕНИЕ ЖЕЛЕЗНЫХ ДОРОГ
Конспект лекций
Часть 2

Редактор Н. А. Майорова
***
 |
Подписано в печать 26.03.2007. Формат 60 × 84.
Плоская печать. Бумага офсетная. Усл. печ. л. 3,6. Уч.-изд. л. 4,0.
Тираж 150 экз. Заказ
**
Редакционно-издательский отдел ОмГУПСа
Типография ОмГУПСа
*
644046, г. Омск, пр. Маркса, 35
|
|
|
|
|
|


