 |
Потенциальная энергия взаимодействия тела с Землей
|
|
|
|
Потенциальная энергия взаимодействия зарядов
Потенциальная энергия взаимодействия двух точечных зарядов равна
q1q2
Wп=k——.
r
Вместо того, чтобы выводить эту формулу, вычислим с её помощью силу взаимодействия точечных заряженных тел; если получим закон Кулона, значит исходная формула верна. Пусть заряд q2 неподвижен, а заряд q1 перемещается на малое расстояние Δr=r2-r1, причём r1»r2»r, тогда силу можно считать постоянной, а r1r2=r2.
A=FΔr=-(Wп2-Wп1),
q1q2 q1q2 r2-r1 q1q2Δr
FΔr=Wп1-Wп1=k—— - k——= kq1q2——=k———.
r1 r2 r1r2 r2
Сокращяя на Δr, получаем закон Кулона, значит приведённая выше формула потенциальной энергии взаимодействия точечных зарядов верна.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел.
Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.
При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.
Силы, работа которых зависит от формы траектории, называются непотенциальными. При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.
Потенциальная энергия взаимодействия тела с Землей
Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg.
|
|
|
Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна
. (5)
Рис. 1
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу
, (6)
где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.
Рис. 2
Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:
, (7)
где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С.
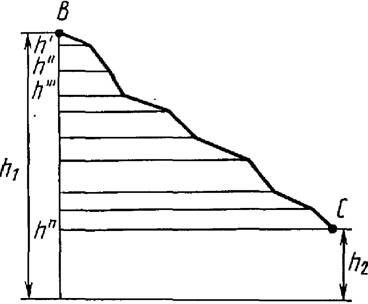
Рис. 3
Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.
При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.
Равенство (7) можно представить в таком виде:
. (8)
Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.
Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2, в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.
|
|
|
. (9)
Потенциальная энергия обозначается буквой Е p.
Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:
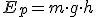. (10)
ДРУГОЙ ВАРИАНТ
Потенциальная энергия 
— скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.
Единицей измерения энергии в СИ является Джоуль.
Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
Ep = mgh,
где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
|
|
|
