 |
Экономико-математическая модель.
|
|
|
|
ЛИНЕЙНЫЕ МОДЕЛИ
Задание 1
Транспортная задача (минимум)
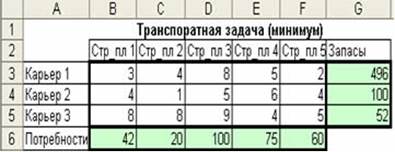
Постановка задачи.
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пятим потребителям (строительным площадкам). Стоимость на доставку включается у себестоимость объекта, что сопровождается, потому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом. Дано: запасы (предложения) песка на карьерах (поставщиков); потребности (спрос) песка стройплощадок (потребителей); затраты (цена) на транспортирования между каждой парой «поставщик-потребитель». Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при котором общие затраты были бы минимальными.
Экономико-математическая модель.
- Найти План перевозок при котором:
- Об_затраты=План*Цена_перевозок - min
- При ограничениях: Ввезено=Потребности; Вывезено<=Запасы и План>=0
Реализация в Excel. Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Об_затраты):

- столбец Вывезено заполняем формулой: =СУММ(План_карьеры);
- строку Ввезено заполняем формулой: =СУММ(План_стр_пл);
- в столбец Остаток вводим формулу: Запас-Вывезено;
- в целевую ячейку (Об_затраты) вводим формулу: =СУММПРОИЗВ(Цена; Пдан).

Запускаем программу Поиск решений командой Данные/Анализ / Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
|
|
|
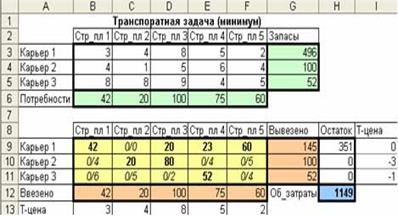
Анализ результатов. Минимальные затраты на транспортирование составляют 1149 д. ед. Нормированная стоимость показывает, до какого значения нужно уменьшить затраты на перевозку, что бы невыгодные маршруты стали выгодными. Теневые цены запасов поставщиков есть отрицательные числа, они показывают, как уменьшиться Об_затраты при увеличении дефицитных запасов поставщиков. Теневые цены потребностей потребителей указывают, как увеличится. Об_затраты при увеличении потребностей.
Задание 2
Расписание
Постановка задачи.
Расписание касается людей или машин, состояние которых на определенном этапе определяются двумя вариантами – человек в определенный день вышел/ не вышел, машина на определенной стадии работает/ не работает т. д. Соответственно, расписание имеет вид комбинаций типу 011100101.
В нашем случае 10 работниц исполняют положение на них функции, на каждый день известны потребности в их численности, при чем установлена 5-дневная рабочая неделя. Нужно определить расписание выхода на роботу, чтобы удовлетворить эти потребности с минимальным количеством чел./день.
Экономико-математическая модель.
- Найти таблицу расписания такую, чтобы
- Чтобы общие количество человек - min
- При ограничениях: Всего задействованных человек = Потребностям в них; количество рабочих дней каждой работницы = 5, а также все неизвестные двоичного типа.
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Количество):
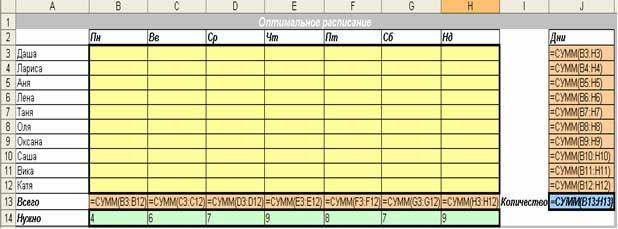
- в столбец Дни вводим формулу сумы по строкам матрицы расписания;
- в строку Всего вводим формулу сумы по столбцам матрицы расписания;
- в целевую ячейку Количество вводим формулу: =СУММ(Всего).

Запускаем программу Поиск решений командой Данные/Анализ / Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
|
|
|
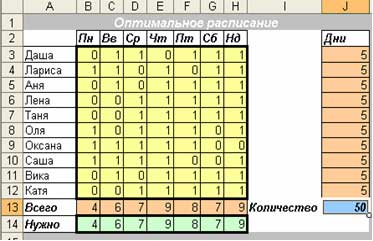
Анализ результатов.
В полученном результате видим, что данное расписание соответствует нашим заданным ограничениям и при котором задействовано наименьшее количество работниц – это значит что наш план оптимальный.
Задание 3
Назначение на должность
Постановка задачи:
Название задачи и соответственной модели – о назначении (assignment problem) – непосредственно исходить от практической кадровой ситуации, когда претендентов нужно назначить на вакантные должности наилучшим образом.
Критерий максимизации общего аффекта используется тогда, когда известны о каждом претенденте заданные оценки способности исполнения определенной функции (чем выше, тем лучше), минимизации – когда, скажем, для каждого претендента заданная величина затрат на его подготовку для определенной деятельности (чем выше, тем хуже).
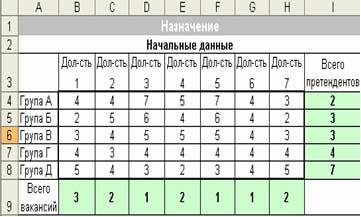
Пример. Предприятие объявило набор работников для нового цеха – указало названия семи должностей и количество вакансий по каждой из них. Кадровая служба собрала от 18 претендентов на эти должности, провела тестирование по каждой из них и за результатами определила 5 групп с одинаковыми оценками и возможностями, получивши соответственную таблицу средних оценок их умений и знаний.
Нужно назначить на вакантные должности претендентов таким образом, что бы общая эффективность исполнения ними соответствующих обязанностей была максимальной.
Особенность – наличие высокой оценки еще не гарантирует успех, поскольку целью оптимизации о назначении есть максимальный общий эффект.
Экономико-математическая модель.
Найти такую матрицу назначений, чтобы
Общий эффект=Матрица_оценок*Матрица_назначений - mах
При ограничениях: Назначено<=Всего_претендентов;
Занято=Всего_вакансий.
|
|
|
Матрица_назначений>=0.
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Об_эффект):
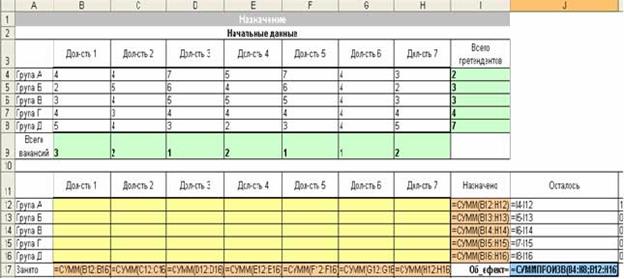
в столбец Назначено вводим формулу сумы по сроках матрицы назначено;
в столбец Осталось вводим формулу Всего претендентов-Назначено;
в строку Занято вводим формулу сумы по столбцах матрицы назначено;
целевую ячейку заполняем формулой: =СУММПРОИЗВ(Матрица_оценок; Матрица_назначений).
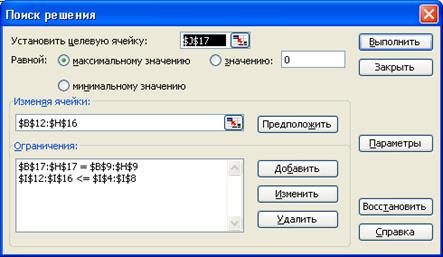
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
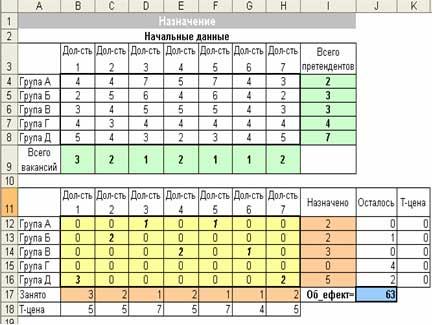
Анализ результатов.
Оптимальный план назначений (смотри таблицу) обеспечивает общую эффективность 63.
Теневые цены для претендентов показывают на сколько изменится целевая ячейка при увеличении данного претендента на 1 ед. Теневые цены для вакансий показывают «ценность» соответствующих должностей.
Нормированные стоимости для нулевых назначений означают:
на сколько нужно увеличить оценку, чтобы можно было претендовать на назначение;
на сколько уменьшиться общая эффективность, если на должность будет назначен этот «невыгодный» претендент.
Задание 4
Инвестиции
|
Постановка задачи.
Инвестор, рискуя, планирует наилучшим образом определить части сумм денег («яйца») общим объемом S д. ед., которые будут вложены у n предприятий («корзины») путем покупки акций с целью получения прибыли у определенном последующем периоде. Условие оптимально означает, что существует два альтернативные критерии оптимизации:
- минимизация риска при фиксированном доходе (аккуратный подход) или
- максимизация дохода при фиксированном риске (риске).
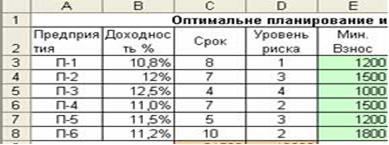
В инвестиционномменеджменте набор частей сумм инвестирования называется портфель, оптимальным портфелем есть такой набор, который инвестор признает для себя наилучшим относительно дохода и риска. Чем больший доход, тем больший риск.Наш инвестор хочет вложить деньги в суме 30000 д. ед. в акции 6 предприятий, для каждого с которых известны доходность акций (%), срок действия, оценка риска, максимальная величина инвестиций на одно предприятие не больше 7500 в предприятия с уровнем риска больше 3 вложить не больше 1/3 сумы всех денег, а в предприятия со сроком больше чем 5 лет не меньше? сумы денег.Инвестор должен выбрать на основе фиксированных предприятиями рисков оптимальный вариант – куда и сколько вложить денег, что бы получить максимальный доход.
|
|
|
Экономико-математическая модель.
- Найти план инвестирования при котором,
- Об_Доход=План*Доходность(%) - mах
- При ограничениях: План=30000; План_предприятие<=7500; План>=Мин_взнос Предприятия(риск>=3) <=10000; Предприятия(срок>5)>=15000.
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Об_Доход):

- столбец Доход заполняем формулами План*Доходность;
- столбец Портфель заполняем формулами План/Об_Доход;
- под столбцом Уровень риска вводим формулу: =СУММЕСЛИ(Риск;>=3;план);
- под столбцом Срок вводим формулу: =СУММЕСЛИ(Срок;>5;план);
- в целевую ячейку Об_Доход вводим формулу: =СУММ(Доход).
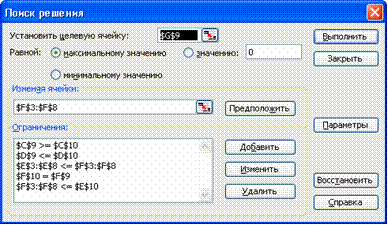
Запускаем программу Поиск решений командой Данные/Анализ / Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
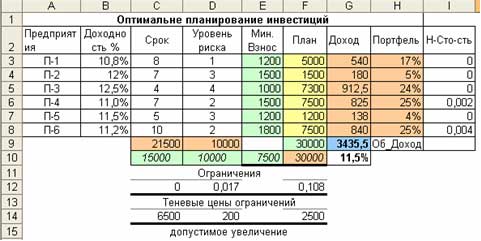
Анализ результатов. Оптимальный план инвестирования (540; 180; 912,5; 825; 138; 840) обеспечит максимальный Доход в размере 3435,5 д. ед., что составило 11,5% сумы инвестиций (не плохо, если идеальный 12,5%). Нормированная стоимость неизвестных (План) указывает, как изменится Об_Доход при принудительном увеличении значения неизвестных. Теневая цена 0,108 для величины инвестиций (30000) указывает на увеличение Об_Дохода почти на 11 копеек при увеличении сумы инвестирования на 1 д. ед. Теневая цена 0,017 для величины ограничения на суму рискованных инвестиций (10000) указывает на увеличение Об_Дохода на эту величину при увеличении ограничения на 1 ед.
|
|
|


