 |
Сопряженные и симметричные линейные операторы в евклидовом пространстве.
|
|
|
|
Занятие 13 (Фдз 14).
Ортогональные операторы в евклидовом пространстве.
Сопряженные и симметричные линейные операторы в евклидовом пространстве.
13.1. Ортогональный оператор и его свойства.
13.2. Сопряженный линейный оператор
13.3. Симметричный (самосопряженный) линейный оператор. Существование и нахождение ортонормированного собственного базиса симметричного линейного оператора.
13.1. Линейный оператор  , заданный в евклидовом пространстве
, заданный в евклидовом пространстве 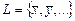 со скалярным произведением
со скалярным произведением 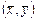 , называется ортогональным оператором, если
, называется ортогональным оператором, если  , где
, где  .
.
Ортогональный оператор не изменяет длин векторов и углов между ними, т.е.
 .
.
В произвольном базисе  пространства
пространства 

 , (1)
, (1)
где  - матрица ортогонального оператора,
- матрица ортогонального оператора,  - матрица Грама,
- матрица Грама, 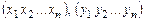 - координаты векторов
- координаты векторов  в базисе
в базисе  . В случае ортонормированного базиса
. В случае ортонормированного базиса 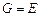 , и равенство (1) заменяется равенством
, и равенство (1) заменяется равенством
 . (2)
. (2)
Следовательно, в любом ортонормированном базисе пространства  ортогональный оператор имеет ортогональную матрицу
ортогональный оператор имеет ортогональную матрицу  .
.
Пример 1. Рассмотрим двумерное евклидово пространство  , содержащее все векторы на декартовой плоскости
, содержащее все векторы на декартовой плоскости  со стандартным скалярным произведением
со стандартным скалярным произведением  . Пусть
. Пусть  - линейный оператор поворота векторов вокруг начала координат
- линейный оператор поворота векторов вокруг начала координат  на заданный угол
на заданный угол  . Доказать, что
. Доказать, что  - ортогональный оператор.
- ортогональный оператор.
Решение.
С геометрической точки зрения ортогональность заданного оператора  очевидна.
очевидна.
Проведем строгое доказательство.
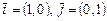 - единичные векторы осей
- единичные векторы осей  . Эти векторы образуют стандартный ортонормированный базис пространства
. Эти векторы образуют стандартный ортонормированный базис пространства  , с которым связано стандартное скалярное произведение.
, с которым связано стандартное скалярное произведение.
 . (3)
. (3)
Рассмотрим два произвольных вектора  .
.

 .
.

 .
.


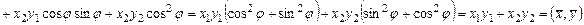 .
.
Т.к.  , делаем вывод:
, делаем вывод:  - ортогональный оператор.
- ортогональный оператор.
В дополнение к проведенному доказательству проверим ортогональность матрицы  оператора
оператора  в ортонормированном базисе
в ортонормированном базисе  . Из формул (3), (2) находим
. Из формул (3), (2) находим
|
|
|
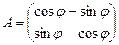 ,
, 
 - ортогональная матрица.
- ортогональная матрица.
Пример 2. Рассмотрим двумерное евклидово пространство 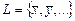 со скалярным произведением
со скалярным произведением  в базисе
в базисе  . Пусть
. Пусть  - линейный оператор, имеющий в базисе
- линейный оператор, имеющий в базисе  матрицу
матрицу  . Требуется выяснить, является ли оператор
. Требуется выяснить, является ли оператор  ортогональным оператором.
ортогональным оператором.
Решение.
Проверим выполнение равенства 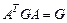 .
.

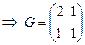 - матрица Грама в базисе
- матрица Грама в базисе  .
.

 не является ортогональным оператором.
не является ортогональным оператором.
13.2. Пусть даны два линейных оператора  и
и  в евклидовом пространстве
в евклидовом пространстве 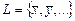 со скалярным произведением
со скалярным произведением 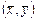 . Оператор
. Оператор  называется сопряженным оператором оператору
называется сопряженным оператором оператору  , если
, если  , где
, где  .
.
Если  и
и  матрицы оператора
матрицы оператора  и сопряженного ему оператора
и сопряженного ему оператора  в базисе
в базисе  пространства
пространства  , и
, и  - матрица Грама скалярного произведения в этом базисе, то
- матрица Грама скалярного произведения в этом базисе, то
 . (4)
. (4)
Указанная связь между матрицами  и
и  позволяет найти матрицу
позволяет найти матрицу  , если известна матрица
, если известна матрица  , и наоборот, найти матрицу
, и наоборот, найти матрицу  , если известна матрица
, если известна матрица  .
.
В ортонормированном базисе, где 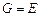 , равенство (4) заменится равенством
, равенство (4) заменится равенством  .
.
Следует отметить, что сопряженный оператор  оператору
оператору  совпадает с оператором
совпадает с оператором  . Поэтому, операторы
. Поэтому, операторы  и
и  называются взаимно сопряженными.
называются взаимно сопряженными.
Пример 3. Рассмотрим двумерное евклидово пространство 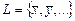 со скалярным произведением
со скалярным произведением  в базисе
в базисе  . Пусть
. Пусть  - линейный оператор, имеющий в базисе
- линейный оператор, имеющий в базисе  матрицу
матрицу  . Потребуем найти матрицу
. Потребуем найти матрицу  сопряженного оператора
сопряженного оператора  в данном базисе. Проверить также, что матрица
в данном базисе. Проверить также, что матрица  оператора
оператора  , сопряженного оператору
, сопряженного оператору  , совпадает с матрицей
, совпадает с матрицей  оператора
оператора  .
.
Решение.

 - матрица Грама в базисе
- матрица Грама в базисе  .
.
Из матричного равенства (5) выводим:  .
.
 .
.
Займемся теперь поиском матрицы  оператора
оператора  . Согласно формуле (5) выводим:
. Согласно формуле (5) выводим:
 .
.
13.3. Пусть  - линейный оператор, действующий в евклидовом пространстве
- линейный оператор, действующий в евклидовом пространстве 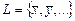 со скалярным произведением
со скалярным произведением 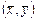 . Оператор
. Оператор  называется самосопряженным или симметричным, если
называется самосопряженным или симметричным, если 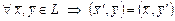 , где
, где  .
.
Если  - матрица оператора
- матрица оператора  в базисе
в базисе  пространства
пространства  , и
, и  - матрица Грама скалярного произведения в этом базисе, то
- матрица Грама скалярного произведения в этом базисе, то
|
|
|
 .
.
В ортонормированном базисе (в котором 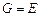 ) это равенство заменится равенством
) это равенство заменится равенством
 .
.
Следовательно, в ортонормированном базисе симметричный оператор имеет симметрическую матрицу.
Важные свойства симметричного оператора фиксирует следующая теорема.
Все собственные значения симметричного оператора действительны, и собственные векторы, отвечающие различным собственным значениям ортогональны.
Из собственных векторов симметричного оператора можно не только образовать собственный базис, но и даже ортонормированный собственный базис. Поэтому, любой симметричный оператор является оператором простого типа (см. занятие 7).
Пример 4. Найти собственный ортонормированный базис симметричного оператора  , действующего в двумерном евклидовом пространстве, если в ортонормированном базисе
, действующего в двумерном евклидовом пространстве, если в ортонормированном базисе  оператор
оператор  имеет матрицу
имеет матрицу  .
.
Решение.
1. Из характеристического уравнения найдем собственные значения оператора  .
.
 .
.
2. Теперь найдем собственные векторы.

 - собственный вектор с собственным значением
- собственный вектор с собственным значением  .
.

 - собственный вектор с собственным значением
- собственный вектор с собственным значением  .
.
В ортонормированном базисе  скалярное произведение задается формулой
скалярное произведение задается формулой
 , где
, где  - координаты векторов
- координаты векторов  в этом базисе.
в этом базисе.

 - ортогональные векторы (что согласуется с выводами теоремы, приведенной выше)
- ортогональные векторы (что согласуется с выводами теоремы, приведенной выше) 
 - линейно независимая система. Т.к. евклидово пространство двумерно, приходим к выводу:
- линейно независимая система. Т.к. евклидово пространство двумерно, приходим к выводу:  - ортогональный собственный базис.
- ортогональный собственный базис.
Чтобы получить ортонормированный собственный базис  нужно пронормировать векторы
нужно пронормировать векторы  .
.
 .
.
 .
.
Итак,  - собственный базис симметричного оператора
- собственный базис симметричного оператора  .
.
Пример 5. Найти собственный ортонормированный базис симметричного оператора  , действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе
, действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе 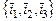 оператор
оператор  имеет матрицу
имеет матрицу
 .
.
Решение.
Найдем собственные значения и собственные матрицы оператора  .
.
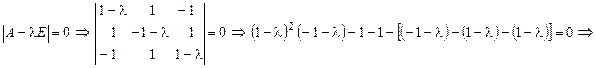
 .
.

 - собственный вектор с собственным значением
- собственный вектор с собственным значением 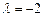 .
.

 - собственный вектор с собственным значением
- собственный вектор с собственным значением  .
.
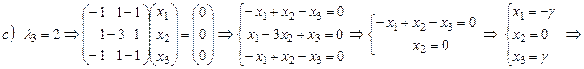
 - собственный вектор с собственным значением
- собственный вектор с собственным значением  .
.
Собственные векторы 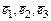 отвечают различным собственным значениям. Следовательно,
отвечают различным собственным значениям. Следовательно,  - ортогональная система векторов и одновременно является собственным ортогональным базисом оператора
- ортогональная система векторов и одновременно является собственным ортогональным базисом оператора  . Чтобы получить собственный ортонормированный базис
. Чтобы получить собственный ортонормированный базис  , пронормируем векторы
, пронормируем векторы 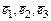 .
.
|
|
|
 .
.
 .
.
 .
.
Пример 6. Найти собственный ортонормированный базис симметричного оператора  , действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе
, действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе 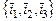 оператор
оператор  имеет матрицу
имеет матрицу  .
.
Решение. Найдем собственные значения и собственные матрицы оператора  .
.
 .
.

 ,
,  .
.
 - два линейно независимых собственных вектора с собственным значением
- два линейно независимых собственных вектора с собственным значением 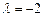 .
.

 - собственный вектор с собственным значением
- собственный вектор с собственным значением  .
.
Собственные векторы 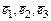 образуют собственный базис оператора
образуют собственный базис оператора  .
.
Этот базис не является ортогональным:
 ортогонален
ортогонален  , т.к.
, т.к.  ,
,
 не ортогонален
не ортогонален  , т.к.
, т.к.  .
.
Линейная оболочка векторов  совпадает с множеством всех собственных векторов с собственным значением
совпадает с множеством всех собственных векторов с собственным значением  и образует линейное подпространство
и образует линейное подпространство  в пространстве
в пространстве  . Система векторов
. Система векторов  служит базисом подпространства
служит базисом подпространства  . Каждый из векторов этой оболочки ортогонален вектору
. Каждый из векторов этой оболочки ортогонален вектору  .
.
Проведем ортогонализацию базиса  подпространства
подпространства  .
.
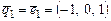 .
.
 ,
,  .
.
Векторы  образуют ортогональный базис подпространства
образуют ортогональный базис подпространства  , а тройка векторов
, а тройка векторов  - ортогональный базис (собственный базис оператора
- ортогональный базис (собственный базис оператора  ) пространства
) пространства  .
.
Пронормировав векторы  , получим собственный ортонормированный базис
, получим собственный ортонормированный базис  .
.
 .
.
 .
.
 .
.
Домашнее задание.
1. В двумерном евклидовом пространстве 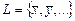 со скалярным произведением
со скалярным произведением  в базисе
в базисе  задан линейный оператор
задан линейный оператор  , имеющий в базисе
, имеющий в базисе  матрицу
матрицу  . Найти матрицу
. Найти матрицу  в базисе
в базисе  оператора
оператора  , сопряженного оператору
, сопряженного оператору  ли оператор
ли оператор  .
.
2. Найти собственный ортонормированный базис симметричного оператора  , действующего в двумерном евклидовом пространстве, если в ортонормированном базисе
, действующего в двумерном евклидовом пространстве, если в ортонормированном базисе  оператор
оператор  имеет матрицу
имеет матрицу  .
.
3. Найти собственный ортонормированный базис симметричного оператора  , действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе
, действующего в трехмерном евклидовом пространстве, если в ортонормированном базисе 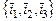 оператор
оператор  имеет матрицу
имеет матрицу  .
.
|
|
|


