 |
Линейные пространства. Замена базиса. Линейные системы. Критерий совместности системы (теорема Кронекера-Капелли).
|
|
|
|
Занятие 1 (Фдз 2).
1.1. Закон преобразования координат вектора при переходе к новому базису. Матрица перехода от старого базиса к новому базису.
1.2. Ранг матрицы. Критерий совместности линейной системы (теорема Кронекера-Капелли).
1.1. Пусть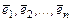 
и 
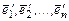- два базиса 
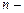мерного линейного пространства 
.
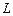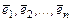- "старый" базис и 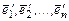- "новый" базис. Они связаны равенствами
,
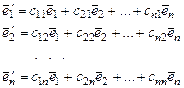которые в матричном виде записываются так: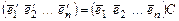 
,
где 
- невырожденная квадратная матрица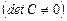 
,
называемая матрицей перехода от "старого" базиса 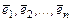к "новому" базису 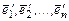. Столбцы матрицы 
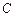- координаты векторов 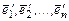в базисе .
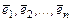Пусть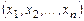 
- координаты вектора 
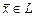в базисе 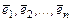и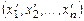 
- координаты вектора 
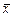в базисе 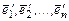, т.е. 
, 
.
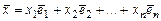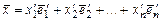Тогда координаты вектора 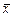в старом и новом базисах связаны равенствами:
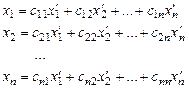или 
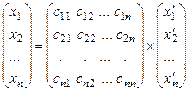. (1)
Формулы (1) называются законом преобразования координат вектора при переходе к новому базису.
Пример 1. Даны два базиса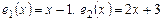 
и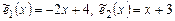 
линейного пространства 
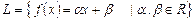. Найти матрицу 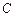перехода от базиса 
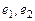к базису 
.
Решение.
1) 
первый столбец матрицы .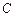
2) 
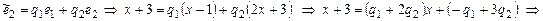
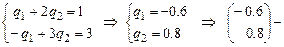второй столбец матрицы .
.
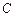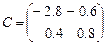Пример 2. Пусть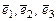 
и 
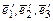- два базиса трехмерного линейного пространства ,
.
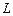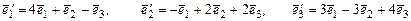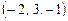- координаты вектора 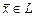в базисе 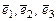. Найти координаты вектора 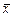в базисе ,
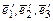Решение.
Сначала найдем матрицу 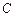перехода от базиса 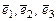к базису .
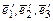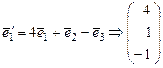- 1-й столбец , 
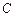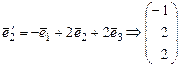- 2-й столбец ,
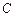- 3-й столбец .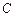 
. 
.
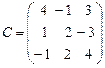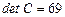Отличие определителя от нуля доказывает невырожденность матрицы 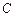(если бы оказалось, что 
, то следовало сделать такой вывод: 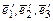не может быть базисом пространства 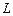и поставленную задачу решить нельзя).
Обозначим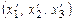 
- координаты вектора 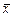в базисе 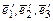. Согласно закону (6) преобразования координат находим,
.
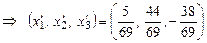Пример 3. Дано линейное пространство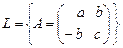 
. Надо доказать, что 
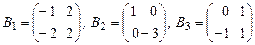и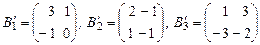 
- базисы этого пространства и найти матрицу 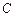перехода от базиса 
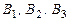к базису 
.
|
|
|
Решение.
Пространство 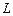имеет стандартный базис 
, поэтому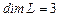 
. Для того, чтобы доказать, что 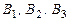и - базисы 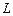достаточно показать линейную независимость этих систем матриц. Предоставляем сделать это читателю.
Здесь же поступим иначе. Найдем разложения матриц 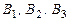и в базисе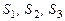 
, из которых определим матрицы 
и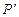 
, связывающие стандартный базис 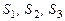с заданными системами матрицами 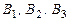и :
, (2)
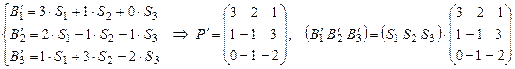. (3)
Вычислим определители матриц , : 
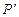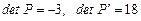. В силу того, что определители оказались не равны нулю, сразу можно сделать вывод: 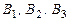и - базисы пространства 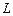. Матрицу 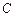перехода от базиса 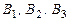к базису найдем, используя матричные равенства (2), (3).
.
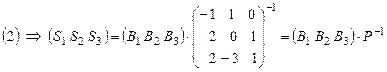
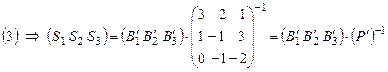
Вычисление элементов матрицы 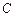предоставляем читателю.
1.2. Рассмотрим теперь линейную систему алгебраических уравнений.
, (
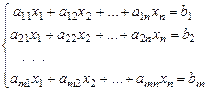-неизвестные) (4)
Напомним, что система называется совместной, если у нее есть хотя бы одно решение. Если же у системы нет ни одного решения, то ее называют несовместной. В 1-м семестре совместность
(несовместность) системы устанавливалась в ходе ее решения методом Гаусса. Ответ на вопрос: совместна или нет заданная система дает также теорема Кронекера-Капелли. Система (4) совместна тогда и только тогда, когда ранг расширенной матрицы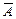 
системы равен рангу матрицы 
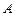системы, т.е.
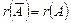, где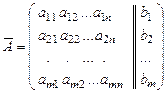 
, 
.
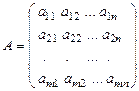Рангом матрицы называется наибольший порядок ненулевого определителя в этой матрице. Ранг матрицы не изменяется, если:
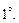В матрице поменять местами две строки (два столбца).
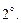Строку (столбец) умножить на число, отличное от нуля.
К строке (столбцу) прибавить другую строку (другой столбец), умноженную (умноженный) на некоторое число.
С помощью действий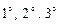 
матрицу можно привести к треугольному виду, из которого легко выделяется ненулевой определитель максимального порядка и находится ранг матрицы.
В случае совместности системы она имеет только одно решение, когда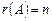 
, если же 
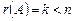, то общее решение системы содержит бесконечно много решений и зависит от 
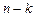параметров.
|
|
|
Пример 4. Найти ранг матрицы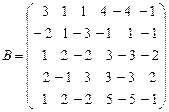 
Решение.
С помощью действий 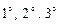приведем матрицу 
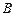к треугольному виду
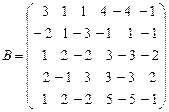
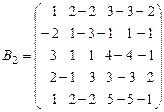
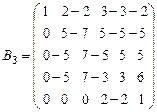
1. В матрице 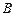переставили местами 1-ю и 3-ю строки, получили матрицу 
.
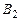2. В матрице 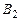: прибавили ко 2-й строке 1-ю строку, умноженную на число 2;
прибавили к 3-й строке 1-ю строку, умноженную на число (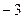
);
прибавили к 4-й строке 1-ю строку, умноженную на число (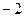
);
прибавили к 5-й строке 1-ю строку, умноженную на число (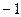
).
Получили матрицу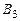 
3. В матрице 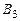: прибавили 2-ю строку к 3-й строке;
прибавили 2-ю строку к 4-й строке. Получили матрицу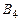 
.
.
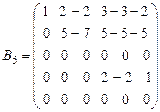
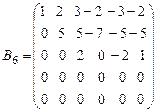4. В матрице 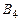прибавили к 5-й строке 4-ю строку, умноженную на число (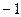). Получили 
.
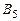5. В матрице 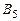сначала переставили местами 3-ю и 4-ю строки, затем переставили местами
3-й и 4-й столбцы. В результате получили матрицу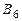 
.
Ранги матриц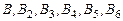 
совпадают. Ранг матрицы 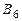равен трем, т.к. у этой матрицы есть определитель третьего порядка (это определитель на пересечении первых трех строк и первых трех столбцов), отличный от нуля:
,
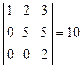а все определители четвертого и пятого порядка содержат нулевую строку, и поэтому равны нулю.
Следовательно,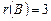 
.
Пример 5. С помощью теоремы Кронекера-Капелли исследовать совместность системы
.
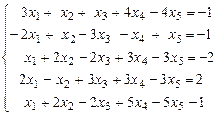Решение.
Найдем одновременно ранги расширенной матрицы 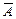и матрицы 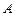данной системы. При этом следует иметь в виду, что последний столбец расширенной матрицы нельзя переставлять местами с другими столбцами. Заметим, что матрица 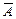совпадает с матрицей 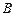из примера 4. Поэтому, нахождение ранга 
в точности повторяет действия, выполненные при нахождении ранга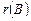 
.
.
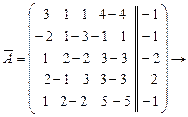
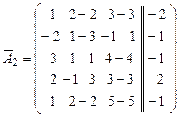
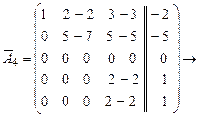
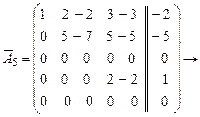
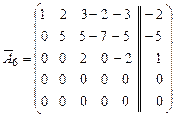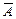. Последний столбец не переставлялся местами с другими столбцами, поэтому по матрице 
, исключая из рассмотрения последний столбец матрицы , находится ранг матрицы 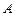системы. 
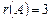. Итак, установлено, что 
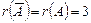. Следовательно, система совместна. У нее число 
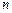неизвестных равно 5, и 
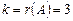. Значит, общее решение системы содержит бесконечно много решений, зависящее от 
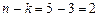параметров.
Пример 6. С помощью теоремы Кронекера-Капелли исследовать совместность системы
.
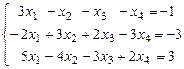Решение.
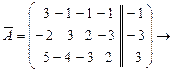
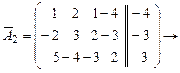
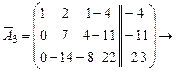
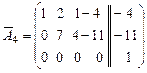
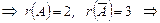система несовместна.
______________________________________________________________________
Домашнее задание.
|
|
|
1. Найти координаты вектора 
, заданного в базисе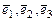 
в новом базисе 
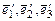, если 
.
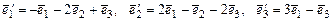2. Найти координаты матрицы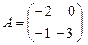 
в стандартном базисе 
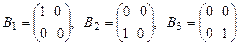и с помощью закона преобразования координат в базисе 
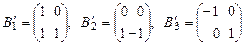линейного пространства 
.
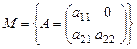3. С помощью теоремы Кронекера-Капелли исследовать совместность следующих линейных систем:
3.1.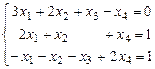 
; 3.2. 
.
|
|
|
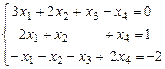