 |
Действия с линейными операторами. Образ, ядро, ранг, дефект линейного оператора.
|
|
|
|
Занятие 4 (Фдз 5).
4.1. Умножение линейного оператора на число, сложение линейных операторов, перемножение линейных операторов. Связь указанных действий с соответствующими операциями над матрицами линейных операторов.
4.2. Условие существования обратного отображения к линейному оператору, его свойства. Матрица обратного оператора, ее нахождение по матрице оператора.
4.3. Ядро и образ линейного оператора, их свойства. Ранг и дефект линейного оператора. Критерий обратимости линейного оператора в терминах его ядра, образа, ранга, дефекта.
4.1. Пусть даны два линейных оператора 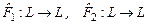 , действующие в одном и том же конечномерном линейном пространстве размерности
, действующие в одном и том же конечномерном линейном пространстве размерности  .
.
По определению.
1) При умножении линейного оператора  на число
на число  получается линейный оператор
получается линейный оператор  , действующий по правилу:
, действующий по правилу:  , где
, где  .
.
2) При сложении линейных операторов  и
и  получается линейный оператор
получается линейный оператор  , действующий по правилу:
, действующий по правилу:  , где
, где  .
.
3) Произведение  линейных операторов
линейных операторов  и
и  также дает линейный оператор
также дает линейный оператор  , действующий по правилу
, действующий по правилу  .
.
Аналогично определяется произведение  :
:  , где
, где  .
.
Отметим, что  и
и  (в общем случае).
(в общем случае).
Пусть  - базис пространства
- базис пространства 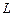 и
и
 - матрицы линейных операторов
- матрицы линейных операторов  ,
,  в базисе
в базисе  .
.
Тогда матрицы операторов  ,
,  ,
,  ,
,  в базисе
в базисе  находятся так:
находятся так:
 - матрица оператора
- матрица оператора  в базисе
в базисе  ;
;
 - матрица оператора
- матрица оператора  в базисе
в базисе  ;
;
 - матрица оператора
- матрица оператора  в базисе
в базисе  ;
;
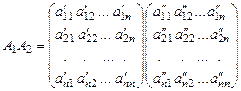 - - матрица оператора
- - матрица оператора  в базисе
в базисе  .
.
Пример 1. Даны два линейных оператора  и
и  :
:
 - оператор поворота векторов на декартовой плоскости
- оператор поворота векторов на декартовой плоскости  (вокруг начала координат против часовой стрелки) на угол
(вокруг начала координат против часовой стрелки) на угол  ;
;
 - оператор проектирования векторов на ось
- оператор проектирования векторов на ось  .
.
Найти матрицы операторов 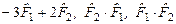 в базисе
в базисе  , где
, где  - единичные векторы на осях
- единичные векторы на осях  .
.
Решение.
Сначала найдем матрицы 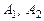 операторов
операторов  в базисе
в базисе  .
.
|
|
|
 - первый столбец матрицы
- первый столбец матрицы  ,
,
 второй столбец матрицы
второй столбец матрицы  . Следовательно,
. Следовательно,  .
.
 - первый столбец матрицы
- первый столбец матрицы  ,
,
 второй столбец матрицы
второй столбец матрицы  . Следовательно,
. Следовательно,  .
.
Обозначим  - матрицы операторов
- матрицы операторов 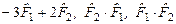 в базисе
в базисе  .
.
Найдем эти матрицы с помощью матриц 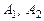 .
.
 .
.
 .
.
 .
.
4.2. В случае, когда линейный оператор  осуществляет взаимно однозначное отображение линейного пространства
осуществляет взаимно однозначное отображение линейного пространства 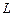 на себя, то существует обратный линейный оператор
на себя, то существует обратный линейный оператор  . Если
. Если  - матрица оператора
- матрица оператора  в базисе
в базисе  пространства
пространства 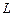 , то матрица оператора
, то матрица оператора  в этом базисе равна
в этом базисе равна  . Следовательно, линейный оператор
. Следовательно, линейный оператор  обратим (имеет обратный оператор
обратим (имеет обратный оператор  ) тогда и только тогда, когда матрица
) тогда и только тогда, когда матрица  оператора
оператора  не вырождена (т.е.
не вырождена (т.е. 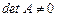 ).
).
Пример 2. Выяснить, какие из линейных операторов  ,
,  примера 1 являются обратимыми?
примера 1 являются обратимыми?
Решение.
Матрица оператора  (в базисе
(в базисе  ) равна
) равна
 .
.  .
.
Следовательно, матрица  не вырождена (отсюда сразу же вытекает, что в любом другом базисе матрица оператора
не вырождена (отсюда сразу же вытекает, что в любом другом базисе матрица оператора  также не вырождена). Оператор
также не вырождена). Оператор  обратим, и матрица обратного оператора
обратим, и матрица обратного оператора  в базисе
в базисе  равна
равна
 .
.
Матрица оператора  (в базисе
(в базисе  ) равна
) равна
 .
.  .
.
Следовательно, матрица  вырождена (отсюда сразу же вытекает, что в любом другом базисе матрица оператора
вырождена (отсюда сразу же вытекает, что в любом другом базисе матрица оператора  также вырождена). Оператор
также вырождена). Оператор  не обратим, и обратного оператора
не обратим, и обратного оператора  не существует.
не существует.
4.3. Ядром линейного оператора  называется множество всех
называется множество всех  , для которых
, для которых  . Для ядра линейного оператора
. Для ядра линейного оператора  принято обозначение
принято обозначение  . Ядро не может быть пустым множеством, т.к.
. Ядро не может быть пустым множеством, т.к.  для любого линейного оператора
для любого линейного оператора  и, значит, нулевой элемент линейного пространства
и, значит, нулевой элемент линейного пространства 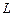 всегда принадлежит множеству
всегда принадлежит множеству  .
.
Образ 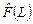 линейного оператора
линейного оператора  и ядро
и ядро  этого оператора являются линейными подпространствами в пространстве
этого оператора являются линейными подпространствами в пространстве 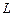 .
.
Рангом  линейного оператора
линейного оператора  называется размерность образа этого оператора. Дефектом
называется размерность образа этого оператора. Дефектом  линейного оператора называется размерность ядра этого оператора. Если
линейного оператора называется размерность ядра этого оператора. Если  , то
, то
 .
.
Если известна матрица  линейного оператора
линейного оператора  в каком-нибудь базисе
в каком-нибудь базисе  , то ранг этого оператора можно найти по рангу матрицы
, то ранг этого оператора можно найти по рангу матрицы  :
:  .
.
|
|
|
Пример 3. Найти ядро, образ, а также ранг и дефект линейного оператора  , где
, где  , и оператор
, и оператор  действует по правилу
действует по правилу
 .
.
Решение.
 . Базис пространства
. Базис пространства  состоит из четырех многочленов. Например, многочлены
состоит из четырех многочленов. Например, многочлены  ,
,  ,
,  ,
,  образуют базис
образуют базис  .
.
Найдем образ  оператора
оператора  .
.
 .
.
 - линейная оболочка трех многочленов
- линейная оболочка трех многочленов 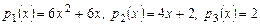 . Эти многочлены представляют полную линейно независимую систему в
. Эти многочлены представляют полную линейно независимую систему в  . Следовательно,
. Следовательно,  - базис
- базис  . Значит,
. Значит,  - ранг оператора
- ранг оператора  .
.
 -дефект оператора
-дефект оператора  .
.
Найдем ядро  оператора
оператора  . Ядро состоит из тех многочленов
. Ядро состоит из тех многочленов  , для которых
, для которых 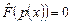 .
.
 .
.
Многочлен тождественно равен нулю (т.е. для всех  ) тогда и только тогда, когда коэффициенты при всех степенях
) тогда и только тогда, когда коэффициенты при всех степенях  равны нулю.
равны нулю.
Следовательно,  .
.
Таким образом, ядро образует множество всех постоянных многочленов.
 - одномерное линейное пространство (его базисом служит
- одномерное линейное пространство (его базисом служит  )
)  . Этот результат подтверждает ранее найденное значение дефекта оператора.
. Этот результат подтверждает ранее найденное значение дефекта оператора.
Ранг  оператора
оператора  можно получить другим способом. Найдем матрицу
можно получить другим способом. Найдем матрицу  оператора
оператора  в базисе
в базисе  ,
,  ,
,  ,
,  пространства
пространства  .
.
 - первый столбец матрицы
- первый столбец матрицы  .
.
 - второй столбец матрицы
- второй столбец матрицы  .
.
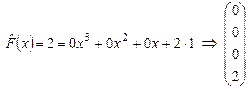 - третий столбец матрицы
- третий столбец матрицы  .
.
 - четвертый столбец матрицы
- четвертый столбец матрицы  .
.
 . Ранг этой матрицы равен трем. Следовательно,
. Ранг этой матрицы равен трем. Следовательно,  .
.
Пример 4. Найти образ, ядро, ранг и дефект линейного оператора  , где
, где  , и оператор
, и оператор  действует по правилу
действует по правилу  , где
, где  .
.
Решение.
Стандартным базисом пространства  служит система матриц
служит система матриц 
 .
.
Найдем образ  оператора
оператора  .
.

 , где
, где  - произвольное число (в силу произвольности чисел
- произвольное число (в силу произвольности чисел  ). Следовательно,
). Следовательно,
 - одномерная линейная оболочка с базисом
- одномерная линейная оболочка с базисом  .
.
 - ранг
- ранг  ,
,  - дефект
- дефект  .
.
Найдем ядро  оператора
оператора  . Нулевым элементом пространства
. Нулевым элементом пространства  является нулевая матрица.
является нулевая матрица.
 .
.
Общее решение полученной системы из одного уравнения с четырьмя неизвестными  (если считать
(если считать  свободными неизвестными) записать в виде
свободными неизвестными) записать в виде
 , где
, где 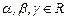 .
.
 - линейная оболочка с базисом
- линейная оболочка с базисом  .
.
Вычислим теперь ранг оператора  по матрице этого оператора. Матрицу
по матрице этого оператора. Матрицу  оператора
оператора  проще всего найти в базисе
проще всего найти в базисе 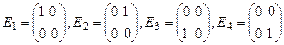 пространства
пространства  .
.
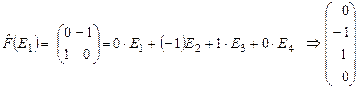 - первый столбец матрицы
- первый столбец матрицы  .
.
 - второй столбец матрицы
- второй столбец матрицы  .
.
 - третий столбец матрицы
- третий столбец матрицы  .
.
 - четвертый столбец матрицы
- четвертый столбец матрицы  .
.
 .
.
Матрица  получена из матрицы
получена из матрицы  так: ко 2-й строке матрицы
так: ко 2-й строке матрицы  прибавили 3-ю строку.
прибавили 3-ю строку.
Ранги матриц  и
и  одинаковы.
одинаковы.  .
.
___________________________________________________________________________
Домашнее задание.
|
|
|
1. Даны два линейных оператора  , действующие в пространстве
, действующие в пространстве  .
.
 - оператор поворота векторов плоскости
- оператор поворота векторов плоскости  против часовой стрелки вокруг начала координат на угол
против часовой стрелки вокруг начала координат на угол  .
.
 - оператор проектирования векторов плоскости
- оператор проектирования векторов плоскости  на прямую
на прямую  .
.
Найти матрицы операторов  в базисе
в базисе  . Указать, какие из операторов
. Указать, какие из операторов  имеют обратный оператор?
имеют обратный оператор?
2. Найти ядро, образ, ранг и дефект линейного оператора
 ,
, 
 .
.
Допускает ли данный оператор обратный оператор  ?
?
3. Найти ядро, образ, ранг и дефект линейного оператора  ,
,
действующего в линейном пространстве 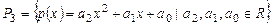 .
.
|
|
|


