 |
Собственные значения и собственные векторы линейного оператора.
|
|
|
|
Занятие 5 (Фдз 6).
5.1. Определение собственного вектора и собственного значения линейного оператора, их геометрический смысл. Главные направления линейного оператора. Примеры нахождения собственных векторов и собственных значений линейного оператора.
5.1. Собственным вектором линейного оператора  называется такой элемент
называется такой элемент  , что
, что  , при этом число
, при этом число  называется собственным числом линейного оператора
называется собственным числом линейного оператора  . Нулевой элемент
. Нулевой элемент  пространства
пространства  исключается из множества собственных векторов по той причине, что
исключается из множества собственных векторов по той причине, что 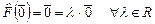 и
и  . Другими словами, элемент
. Другими словами, элемент  не выявляет каких-либо различий у различных линейных операторов.
не выявляет каких-либо различий у различных линейных операторов.
Если  - векторное пространство, то собственный вектор приобретает ясный геометрический смысл:
- векторное пространство, то собственный вектор приобретает ясный геометрический смысл: 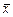 - собственный вектор оператора
- собственный вектор оператора  тогда и только тогда, когда его образ
тогда и только тогда, когда его образ  параллелен вектору
параллелен вектору 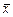 (т.к.
(т.к.  ).
).
Если 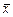 - собственный вектор оператора
- собственный вектор оператора 
 , то вектор
, то вектор  при любом значении постоянной
при любом значении постоянной  также является собственным вектором оператора
также является собственным вектором оператора  с тем же собственным значением
с тем же собственным значением  , которое отвечает вектору
, которое отвечает вектору 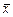 . Действительно,
. Действительно,
 .
.
Таким образом, собственный вектор 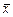 с собственным значением
с собственным значением  оператора
оператора  определяет в пространстве
определяет в пространстве  прямую, образованную векторами
прямую, образованную векторами  и называемую главным направлением оператора
и называемую главным направлением оператора  с собственным значением
с собственным значением  .
.
Одной из основных задач теории линейных операторов является задача по нахождении собственных значений, собственных значений и главных направлений заданного линейного оператора.
Пример 1. Найти собственные значения, собственные векторы, главные направления линейного оператора  , действующего в линейном пространстве
, действующего в линейном пространстве 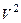 векторов на декартовой плоскости
векторов на декартовой плоскости  следующим образом:
следующим образом:  проектирует векторы на ось
проектирует векторы на ось  .
.
Решение.
Собственные векторы и отвечающие им собственные значения заданного линейного оператора легко определяются, исходя из геометрического смысла собственного вектора и геометрии действия оператора.
|
|
|
Рассмотрим единичные векторы 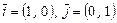 на осях
на осях  и
и  соответственно. Эти векторы образуют базис пространства
соответственно. Эти векторы образуют базис пространства 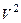 .
.

 - собственный вектор оператора
- собственный вектор оператора  с собственным значением
с собственным значением  .
.

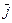 - собственный вектор оператора
- собственный вектор оператора  с собственным значением
с собственным значением  .
.
Главными направлениями оператора  являются:
являются:
ось  (с собственным значение
(с собственным значение  ) и ось
) и ось  (с собственным значением
(с собственным значением  ).
).
Пример 2. Найти собственные значения, собственные векторы, главные направления линейного оператора  , действующего в линейном пространстве
, действующего в линейном пространстве 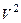 векторов на декартовой плоскости
векторов на декартовой плоскости  следующим образом:
следующим образом:  поворачивает каждый вектор
поворачивает каждый вектор  на угол
на угол  против часовой стрелки вокруг начала координат – точки
против часовой стрелки вокруг начала координат – точки  .
.
Решение.
Собственные векторы у этого оператора есть только при двух значениях угла  :
:  и
и  .
.
1) Если  , то заданный оператор
, то заданный оператор  является тождественным отображением.
является тождественным отображением.
 . Следовательно, любой ненулевой вектор плоскости
. Следовательно, любой ненулевой вектор плоскости  является собственным вектором линейного оператора
является собственным вектором линейного оператора  с собственным значением
с собственным значением  , и любая прямая, проходящая через начало координат, будет главным направлением оператора
, и любая прямая, проходящая через начало координат, будет главным направлением оператора  с собственным значением
с собственным значением  .
.
2) Если  , то оператор
, то оператор  осуществляет отображение по закону:
осуществляет отображение по закону:
 . Следовательно, любой ненулевой вектор плоскости
. Следовательно, любой ненулевой вектор плоскости  является собственным вектором линейного оператора
является собственным вектором линейного оператора  с собственным значением
с собственным значением  , и любая прямая, проходящая через начало координат, служит главным направлением оператора
, и любая прямая, проходящая через начало координат, служит главным направлением оператора  с собственным значением
с собственным значением  .
.
3) Если  , то такой оператор поворота векторов не имеет ни одного собственного вектора. В этом случае,
, то такой оператор поворота векторов не имеет ни одного собственного вектора. В этом случае,  вектор
вектор  не параллелен вектору
не параллелен вектору  , и значит, не существует числа
, и значит, не существует числа  такого, что
такого, что 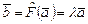 .
.
Пример 3. Найти собственные значения, собственные векторы, главные направления линейного оператора  , действующего в линейном пространстве
, действующего в линейном пространстве 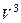 векторов декартова пространства
векторов декартова пространства  следующим образом:
следующим образом:  проектирует каждый вектор
проектирует каждый вектор  на плоскость
на плоскость  .
.
|
|
|
Решение.
Также как и в примерах выше, собственные векторы и отвечающие им собственные значения заданного линейного оператора легко находятся из геометрического смысла собственного вектора.
1) Если вектор  лежит на плоскости
лежит на плоскости  (или параллелен этой плоскости), то
(или параллелен этой плоскости), то  . Значит, любой такой вектор является собственным вектором линейного оператора
. Значит, любой такой вектор является собственным вектором линейного оператора  , с собственным значением
, с собственным значением  . Указанные векторы
. Указанные векторы  имеют координаты
имеют координаты  .
.
Соответственно, главными направлениями с собственным значением  является множество всех прямых в плоскости
является множество всех прямых в плоскости  , проходящих через начало координат.
, проходящих через начало координат.
2) Другими собственными векторами рассматриваемого оператора будут все векторы  , параллельные оси
, параллельные оси  . Для них
. Для них  , т.е. векторы
, т.е. векторы  - собственные векторы линейного оператора
- собственные векторы линейного оператора  с собственным значением
с собственным значением  . Указанные векторы
. Указанные векторы  имеют координаты
имеют координаты  .
.
Соответственно, главным направлением со значением  является ось
является ось  .
.
Других собственных векторов, отличных от указанных выше, у оператора  нет.
нет.
Пример 4. Найти собственные значения и собственные векторы линейного оператора  , действующего в линейном пространстве
, действующего в линейном пространстве 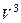 векторов декартова пространства
векторов декартова пространства  следующим образом:
следующим образом:  зеркально отражает каждый вектор пространства от плоскости
зеркально отражает каждый вектор пространства от плоскости  .
.
Решение.
1) Любой вектор  , направленный перпендикулярно плоскости
, направленный перпендикулярно плоскости  , при зеркальном отражении от этой плоскости изменяет свое направление на противоположное, не меняя при этом своей длины. Т.е.
, при зеркальном отражении от этой плоскости изменяет свое направление на противоположное, не меняя при этом своей длины. Т.е.  . Следовательно, все такие векторы
. Следовательно, все такие векторы  - собственные векторы с собственным значением
- собственные векторы с собственным значением  . Из уравнения плоскости легко находится вектор
. Из уравнения плоскости легко находится вектор  , перпендикулярный этой плоскости. Т.к.
, перпендикулярный этой плоскости. Т.к.  параллелен
параллелен  , то
, то  , где
, где  . Таким образом, множество всех собственных векторов линейного оператора
. Таким образом, множество всех собственных векторов линейного оператора  с собственным значением
с собственным значением  образуют векторы с координатами
образуют векторы с координатами  , где
, где  .
.
2) Теперь рассмотрим векторы  , лежащие в (или параллельные) плоскости
, лежащие в (или параллельные) плоскости  . Эти векторы при зеркальном отражении от указанной плоскости не меняются, т.е.
. Эти векторы при зеркальном отражении от указанной плоскости не меняются, т.е.  . Значит векторы
. Значит векторы  - собственные векторы линейного оператора
- собственные векторы линейного оператора  с собственным значением
с собственным значением  .
.
Других собственных векторов у заданного линейного оператора нет.
Пример 5. Найти собственные значения и собственные векторы линейного оператора  , действующего в линейном пространстве
, действующего в линейном пространстве 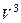 векторов декартова пространства
векторов декартова пространства  следующим образом:
следующим образом:  поворачивает каждый вектор на
поворачивает каждый вектор на  вокруг прямой
вокруг прямой  , проходящей через начало координат
, проходящей через начало координат  .
.
|
|
|
Решение.
Рассмотрим сначала векторы  , лежащие на заданной прямой. Эти векторы параллельны направляющему вектору
, лежащие на заданной прямой. Эти векторы параллельны направляющему вектору  , и значит, имеют координаты
, и значит, имеют координаты  , где
, где  .
.
Под действием оператора  векторы
векторы  переходят в себя, т.е.
переходят в себя, т.е.  .
.
Следовательно, векторы  - собственные векторы линейного оператора
- собственные векторы линейного оператора  с собственным значением
с собственным значением  .
.
Другими собственными векторами оператора  будут векторы
будут векторы  , перпендикулярные прямой
, перпендикулярные прямой  . Под действием
. Под действием  векторы
векторы  переходят в векторы
переходят в векторы  , т.е.
, т.е.  .
.
Следовательно, векторы  - собственные векторы линейного оператора
- собственные векторы линейного оператора  с собственным значением
с собственным значением  .
.
Если обозначить координаты векторов  через
через  , то возможные значения этих координат найдутся из условия ортогональности векторов
, то возможные значения этих координат найдутся из условия ортогональности векторов  и
и  , и будут представлять ненулевые решения уравнения
, и будут представлять ненулевые решения уравнения  .
.
Пример 6. Найти собственные значения и собственные векторы линейного оператора  , действующего в линейном пространстве
, действующего в линейном пространстве 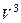 векторов декартова пространства
векторов декартова пространства  следующим образом:
следующим образом:  проектирует каждый вектор на прямую
проектирует каждый вектор на прямую  .
.
Решение.
Векторы  , лежащие на прямой
, лежащие на прямой  , являются собственными векторами оператора
, являются собственными векторами оператора  с собственным значением
с собственным значением  . Оператор
. Оператор  не меняет эти векторы.
не меняет эти векторы.  .
.
Векторы  , перпендикулярные прямой
, перпендикулярные прямой  , проектируются в точку (т.е. нулевой вектор) на этой прямой.
, проектируются в точку (т.е. нулевой вектор) на этой прямой.  . Следовательно, векторы
. Следовательно, векторы  - собственные векторы линейного оператора
- собственные векторы линейного оператора  с собственным значением
с собственным значением  .
.
Пример 7. Найти собственные значения и собственные векторы линейного оператора  , где
, где  , и оператор
, и оператор  действует по правилу
действует по правилу  , где
, где  .
.
Решение.
Данный линейный оператор рассматривался в примере 4 занятия 4. Там установлено, что
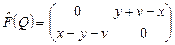 .
.
Согласно определению собственного вектора линейного оператора ненулевая матрица 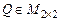 будет собственной матрицей (вектором) оператора
будет собственной матрицей (вектором) оператора  , если
, если  , т.е. когда
, т.е. когда  .
.
Из 1-го и 4-го уравнений полученной системы видно, что  , либо
, либо  .
.
Рассмотрим первый случай:  . Из уравнений системы выводим
. Из уравнений системы выводим
 , где
, где  .
.
Следовательно, собственными матрицами линейного оператора  со значением
со значением  являются все матрицы из ядра
являются все матрицы из ядра  этого оператора.
этого оператора.
|
|
|
Рассмотрим второй случай:  . Теперь из уравнений системы выводим
. Теперь из уравнений системы выводим
 . (*)
. (*)
Здесь в свою очередь: либо  ; либо
; либо  .
.
1) Если  , то из системы (*) находим:
, то из системы (*) находим:  , где
, где  . Учитывая, что в рамках второго случая
. Учитывая, что в рамках второго случая  , заключаем: матрицы вида
, заключаем: матрицы вида  являются собственными матрицами линейного оператора
являются собственными матрицами линейного оператора  с собственным значением
с собственным значением  .
.
2) Если же  , то из системы (*) находим:
, то из системы (*) находим: 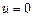 . В результате получили нулевую матрицу
. В результате получили нулевую матрицу  , которая по определению не включается в множество собственных векторов линейного оператора
, которая по определению не включается в множество собственных векторов линейного оператора  .
.
Других собственных матриц у линейного оператора  нет.
нет.
__________________________________________________________________
Домашнее задание.
1. Исходя из геометрии действия линейного оператора, найти собственные векторы и собственные значения следующих линейных операторов:
1.1. Оператора проектирования векторов на плоскость 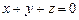 ;
;
1.2. Оператора отражения векторов от оси  ;
;
1.3. Оператора поворота векторов на  вокруг оси
вокруг оси  .
.
2. Используя определение собственного вектора и собственного значения оператора найти собственные векторы и собственные значения следующих линейных операторов.
2.1.  ,
,  ,
,  .
.
2.2.  ,
,  ,
,  .
.
2.3.  ,
, 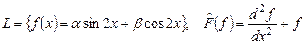 .
.
|
|
|


