 |
Нахождение собственных значений и собственных векторов линейного оператора.
|
|
|
|
Занятие 6 (Фдз 7).
6.1. Характеристическая матрица, характеристический многочлен и характеристическое уравнение. Нахождение собственных значений из характеристического уравнения и собственных векторов из однородной системы уравнений с характеристической матрицей.
6.1. Собственные значение и собственные векторы линейного оператора  обычно находят по матрице оператора.
обычно находят по матрице оператора.
Пусть  ;
;  - базис линейного пространства
- базис линейного пространства  ;
;  - координаты вектора
- координаты вектора 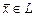 в базисе
в базисе  ;
;
 - матрица оператора
- матрица оператора  в базисе
в базисе  ;
;  - единичная матрица.
- единичная матрица.

 называется характеристической матрицей.
называется характеристической матрицей.
Определитель  после его вычисления дает
после его вычисления дает
многочлен степени  относительно переменной
относительно переменной  . Полученный многочлен называется характеристическим многочленом.
. Полученный многочлен называется характеристическим многочленом.
Уравнение
 (1)
(1)
называется характеристическим уравнением. Это уравнение позволяет найти все собственные числа (значения) оператора  (и действительные и комплексные), они называются также собственными числами матрицы
(и действительные и комплексные), они называются также собственными числами матрицы  .
.
Таким образом, собственные числа – корни характеристического уравнения. Следует особо отметить, что собственные числа оператора  не зависят от базиса, они одни и те же в любом базисе пространства
не зависят от базиса, они одни и те же в любом базисе пространства  .
.
Ниже будем искать только действительные собственные числа оператора  и отвечающие им собственные векторы.
и отвечающие им собственные векторы.
После того, как характеристическое уравнение решено, и действительные собственные числа 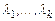 оператора
оператора  найдены, собственные векторы оператора
найдены, собственные векторы оператора  (они называются также собственными векторами матрицы
(они называются также собственными векторами матрицы  ) находятся из систем линейных уравнений, матричное представление которых имеет вид:
) находятся из систем линейных уравнений, матричное представление которых имеет вид:
 . (2)
. (2)
Множество всех ненулевых решений системы (2) – собственные векторы линейного оператора  (матрицы
(матрицы  ) с собственным значением
) с собственным значением  .
.
|
|
|
Пример 1. Найти собственные значения и собственные векторы матрицы  .
.
Решение.
Запишем характеристическое уравнение
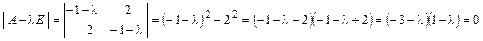 .
.
 - корни кратности 1 характеристического многочлена. Это - собственные числа матрицы
- корни кратности 1 характеристического многочлена. Это - собственные числа матрицы  .
.
Найдем собственные векторы, отвечающие собственному числу  .
.

 - все собственные векторы матрицы с собственным числом
- все собственные векторы матрицы с собственным числом  . Все эти векторы находятся по вектору
. Все эти векторы находятся по вектору 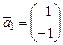 , умножением на произвольное число
, умножением на произвольное число  . Поэтому, в качестве собственного вектора матрицы
. Поэтому, в качестве собственного вектора матрицы  с собственным значением
с собственным значением  в ответе обычно указывается вектор
в ответе обычно указывается вектор  .
.
Найдем теперь собственные векторы, отвечающие собственному числу  .
.

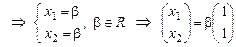 - все собственные векторы матрицы с собственным числом
- все собственные векторы матрицы с собственным числом  . Здесь вектор
. Здесь вектор  служит "определяющим" собственным вектором матрицы
служит "определяющим" собственным вектором матрицы  , отвечающим собственному числу
, отвечающим собственному числу  данной матрицы.
данной матрицы.
Пример 2. Найти собственные значения и собственные векторы матрицы  .
.
Решение.
Запишем характеристическое уравнение
 .
.
Это уравнение имеет два комплексных корня  , где
, где  . Таким образом, собственные числа матрицы
. Таким образом, собственные числа матрицы  - комплексные числа
- комплексные числа 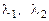 . Обычно ограничиваются нахождением действительных собственных чисел матрицы и соответствующих им собственных векторов. Ответ в этом случае таков: заданная матрица не имеет ни одного действительного собственного числа, и значит, не имеет собственных векторов с действительными координатами.
. Обычно ограничиваются нахождением действительных собственных чисел матрицы и соответствующих им собственных векторов. Ответ в этом случае таков: заданная матрица не имеет ни одного действительного собственного числа, и значит, не имеет собственных векторов с действительными координатами.
Однако у матрицы  имеются собственные векторы с комплексными координатами. Найдем их.
имеются собственные векторы с комплексными координатами. Найдем их.
Сначала найдем собственные векторы, отвечающие собственному числу  .
.
 .
.
Если 2-е уравнение полученной системы умножить на  , то получим 1-е уравнение этой системы. Поэтому, система эквивалентна системе
, то получим 1-е уравнение этой системы. Поэтому, система эквивалентна системе  из одного уравнения.
из одного уравнения.
Положим в ней  , получим
, получим  . Следовательно,
. Следовательно,  - собственный вектор матрицы
- собственный вектор матрицы  , отвечающий собственному числу
, отвечающий собственному числу  . Все другие собственные векторы с данным собственным значением получаются из вектора
. Все другие собственные векторы с данным собственным значением получаются из вектора  , умножением на произвольное комплексное число
, умножением на произвольное комплексное число  .
.
|
|
|
Найдем теперь собственные векторы, отвечающие собственному числу  .
.
 .
.
Положим  , получим
, получим  . Следовательно,
. Следовательно,  - собственный вектор матрицы
- собственный вектор матрицы  , отвечающий собственному числу
, отвечающий собственному числу  . Все другие собственные векторы с данным собственным значением получаются из вектора
. Все другие собственные векторы с данным собственным значением получаются из вектора  , умножением на произвольное комплексное число
, умножением на произвольное комплексное число  .
.
Пример 3. Найти собственные значения и собственные векторы матрицы  .
.
Решение.
Собственные числа матрицы  найдем из характеристического уравнения
найдем из характеристического уравнения
 .
.
 - корень кратности 2 и
- корень кратности 2 и  - корень кратности 1 характеристического уравнения.
- корень кратности 1 характеристического уравнения.
Найдем собственные векторы, отвечающие собственному числу  .
.

 - все собственные векторы.
- все собственные векторы.
"Определяющий" собственный вектор для числа  – вектор
– вектор  .
.
Найдем теперь собственные векторы, отвечающие собственному числу  .
.

 - все собственные векторы.
- все собственные векторы.
"Определяющий" собственный вектор для числа  – вектор
– вектор  .
.
Пример 4. Найти собственные значения и собственные векторы линейного оператора  , где
, где  , если оператор
, если оператор  действует по правилу
действует по правилу  , где
, где 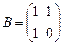 .
.
Решение.
Поставленная задача уже была решена в примере 7 занятия 5 исходя из определений собственного вектора и собственного значения линейного оператора. Здесь приведем другое решение, основывающееся на матрице оператора и характеристическом уравнении.
1) Найдем матрицу  оператора
оператора  в стандартном базисе пространства
в стандартном базисе пространства  :
:
 .
.
 .
.
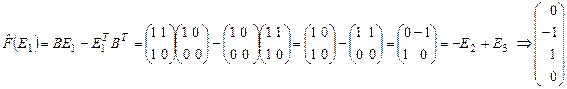 ,
,
 ,
,
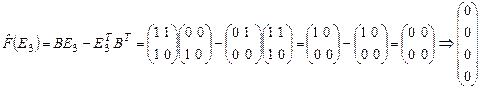 ,
,
 .
.
Полученные столбцы приводят к следующей матрице  .
.
Характеристическое уравнение:
 .
.
Его корни  - собственные значения оператора
- собственные значения оператора  .
.
2) Найдем собственные векторы, отвечающие собственному числу  .
.


 - собственные векторы матрицы с собственным числом
- собственные векторы матрицы с собственным числом  , они представляют линейную комбинацию трех "определяющих" собственных векторов:
, они представляют линейную комбинацию трех "определяющих" собственных векторов:  .
.
Вектор  эквивалентен матрице
эквивалентен матрице  .
.
Вектор  эквивалентен матрице
эквивалентен матрице 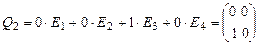 .
.
Вектор  эквивалентен матрице
эквивалентен матрице  .
.
Таким образом, собственному числу  оператора
оператора  отвечают собственные матрицы:
отвечают собственные матрицы:  .
.
3) Теперь найдем собственные векторы матрицы  для числа
для числа  .
. 
 - все собственные векторы матрицы с собственным числом
- все собственные векторы матрицы с собственным числом  . Они представляют линейную комбинацию на векторе:
. Они представляют линейную комбинацию на векторе:  , который приводит к матрице
, который приводит к матрице
 .
.
Итог: собственному числу  оператора
оператора  отвечают собственная матрица
отвечают собственная матрица  .
.
Сравнение полученных результатов с результатами примера 7 занятия 5 показывает их полную идентичность.
|
|
|
Пример 5. Найти собственные значения и собственные векторы линейного оператора  , где
, где 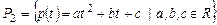 , и оператор
, и оператор  действует по правилу
действует по правилу 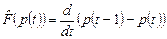 .
.
Решение.
 .
.
 . (3)
. (3)
Найдем теперь матрицу  оператора
оператора  в стандартном базисе
в стандартном базисе  пространства
пространства  .
.
Полагая  из (3) находим
из (3) находим
 - первый столбец матрицы
- первый столбец матрицы  .
.

 - второй столбец матрицы
- второй столбец матрицы  .
.
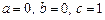
 - третий столбец матрицы
- третий столбец матрицы  .
.
 - собственные числа матрицы
- собственные числа матрицы  и одновременно собственные значения линейного оператора
и одновременно собственные значения линейного оператора  .
.
 .
.
Собственному вектору  отвечает многочлен
отвечает многочлен  .
.
Собственному вектору 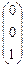 отвечает многочлен
отвечает многочлен  .
.
Следовательно, многочлены вида  являются собственными многочленами (отвечающими собственному значению
являются собственными многочленами (отвечающими собственному значению  ) заданного линейного оператора
) заданного линейного оператора  .
.
_____________________________________________________________________
Домашнее задание.
1. Найти собственные значения и собственные векторы матриц
1.1.  , 1.2.
, 1.2. 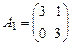 , 1.3.
, 1.3. 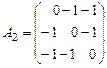 .
.
2. Найти собственные значения и собственные векторы линейного оператора  , где
, где 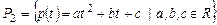 , и оператор
, и оператор  действует по правилу
действует по правилу  . Провести решение с помощью матрицы оператора в стандартном базисе
. Провести решение с помощью матрицы оператора в стандартном базисе  пространства
пространства  .
.
|
|
|


