 |
Линейные, билинейные и квадратичные функции в линейном пространстве.
|
|
|
|
Занятие 8 (Фдз 9).
8.1. Линейная функция в линейном пространстве и ее представление в заданном базисе.
8.2. Билинейная функция в линейном пространстве и соответствующая ей билинейная форма в заданном базисе. Векторно-матричная запись билинейной формы. Матрица билинейной формы, закон ее изменения при переходе к новому базису и инвариантность ранга этой матрицы.
8.3. Квадратичная функция в линейном пространстве. Симметричные билинейные функции и соответствующие им квадратичные функции. Квадратичные функции и соответствующие им квадратичные формы. Матрица квадратичной формы.
8.1. Пусть 
- 
-мерное линейное пространство. Линейной функцией 
на этом пространстве называется отображение векторов 
на вещественную ось 
, обладающее свойством линейности:
или
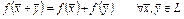и 
. (1)
Если 
- базис пространства 
и 
- координаты вектора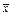 
в базисе 
, то
, где 
.
Пример 1. На линейном векторном пространстве 
заданы две числовые функции 
. Проверить, есть ли среди них линейные функции.
Решение.
.
.
Согласно (2) функция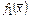 
не является линейной функцией.
,
.
.
Выполнены оба свойства (2). Следовательно,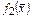 
- линейная функция.
Пример 2. 
. 
стандартный базис пространства . На этом пространстве задана линейная функция 
такая, что
. Найти 
, если 
.
Решение.
.
.
8.2. Билинейной функцией на линейном пространстве называется числовая функция 
линейная по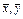 
одновременно, т.е.
; (2)
. (3)
В базисе пространства билинейная функция принимает вид
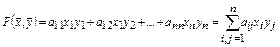, (4)
где 
, и 
- координаты векторов 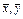в базисе .
Выражение 
называется билинейной формой координат и .
Если 
, то билинейная функция называется симметричной.
Билинейную форму можно записать в векторно-матричной форме
|
|
|
, (5)
где 
.
Матрица 
называется матрицей билинейной формы или матрицей билинейной функции в базисе .
У симметричной билинейной формы матрица симметрична 
. Соответствующая форма (5) называется симметричной билинейной формой.
При переходе к новому базису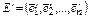 
пространства , в котором координаты векторов 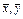соответственно равны 
и 
билинейная функция представляется билинейной формой
,
в которой 
.
Матрицы и 
связаны между собой равенством
. (6)
Здесь 
- матрица перехода от базиса к базису 
.
Пример 3. На линейном векторном пространстве заданы две числовые функции 
. Проверить, есть ли среди них билинейные функции.
Решение.
Пусть
,
.
1) Исследуем функцию 
. Сначала проверим линейность функции по первому аргументу.
.
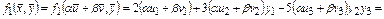
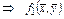линейна по первому аргументу.
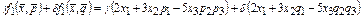Теперь проверим линейность функции по второму аргументу.
.
.
не линейна по второму аргументу.
Окончательный вывод: функция не является билинейной функцией.
2) Исследуем функцию 
. Сначала проверим линейность функции 
по первому аргументу.
линейность по первому аргументу.
Теперь проверим линейность функции по второму аргументу.
линейность по второму аргументу.
Окончательный вывод: - билинейная функция.
В дополнение приведем векторно-матричное выражение для и ее матрицу.
.
Здесь 
.
Следовательно,
- матрица билинейной функции в базисе 
.
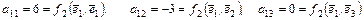и т.д.
Пример 4. Билинейная функция 
на двумерном линейном пространстве в базисе
представлена следующей билинейной формой,
, где 
- координаты векторов 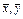в базисе .
Найти выражение функции и матрицу этой функции в базисе 
, если 
.
Решение.
, где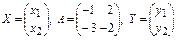 
.
- матрица функции в базисе .
Найдем матрицу перехода от базиса к базису
-1-й столбец матрицы . 
- 2-й столбец .
.
По формуле (6) вычисляем матрицу билинейной функции в базисе .
.
В базисе билинейная функция имеет следующее выражение
.
Здесь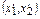 
, 
- координаты векторов 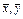в базисе .
|
|
|
8.3. Квадратичной функцией 
на - мерном линейном пространстве называется билинейная функция при совпадающих аргументах, т.е. при 
.
Следовательно, 
. В базисе пространства
.
В найденном выражении функции 
, слагаемые 
и 
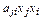
представляют подобные члены: 
. Поэтому,
, где 
при 
и 
.
Выражение квадратичной функции в виде 
называется квадратичной формой.
Пример 5. Найти квадратичные формы соответствующие билинейным формам:
; 
.
Решение.
1) 
.
2) 
.
Следует отметить, что две различные билинейные формы могут давать одну и ту же квадратичную форму. Например, билинейные формы
,
приводят к одинаковой квадратичной форме
.
Таким образом, между билинейными и квадратичными формами не существует взаимно однозначного соответствия. Однако, если рассматривать только симметричные билинейные формы , то между этими формами и соответствующими им квадратичными формами 
автоматически устанавливается взаимно однозначное соответствие.
Каждой квадратичной форме можно поставить в соответствие симметричную матрицу 
, в которой 
. Такое соответствие взаимно однозначно (биективно) отображает множество всех квадратичных форм на множество симметричных матриц. Матрицу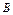 
называют матрицей квадратичной формы.
Пример 6. Найти матрицы квадратичных форм
, 
.
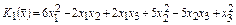Решение.
1) 
.
- матрица квадратичной формы 
.
2) 
.
- матрица квадратичной формы 
.
С помощью матрицы 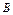квадратичной формы эту квадратичную форму можно переписать в следующей векторно-матричной форме
.
Пример 7. Записать квадратичные формы
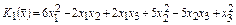, в векторно-матричной форме.
Решение.
Воспользуемся матрицами 
квадратичных форм и , найденными в примере 6.
.
При переходе к новому базису 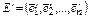, с которым связаны координаты , квадратичная форма меняется по закону
,
где 
, 
- матрица квадратичной формы в новом базисе, ее получают из матрицы 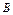с помощью формулы 
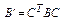, в которой - матрица перехода от старого базиса к новому базису ( - невырожденная матрица, ее определитель отличен от нуля).
Напомним, что старые и новые координаты связаны равенством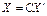 
или
.
Эти формулы называются невырожденным линейным преобразованием координат.
_______________________________________________________________
Домашнее задание.
|
|
|
1. Билинейные формы 
, 
в базисе 
имеет вид
1.1. 
.
1.2. 
.
Найти матрицу билинейной формы, ее матричное представление, а также матрицу и выражение в новом базисе 
.
2. Найти квадратичные формы, соответствующие билинейным формам
из примеров 1.1, 1.2. Записать эти квадратичные формы в матричном виде. По квадратичным формам записать соответствующие им симметричные билинейные формы.
|
|
|
