 |
Сопряжение двух дуг окружности дугой заданного радиуса.
|
|
|
|
Форма 1

Форма 2

Форма 2а

Сопряжения-теоритический материал для выполнения задания
Плавный переход прямой линии в дугу или одной дуги в другую называют сопряжением. Для построения сопряжения надо найти центры, из которых проводят дуги, т. е. центры сопряжений (рис.3). Затем нужно найти точки, в которых одна линия переходит в другую, т. е. точки сопряжений. При построении контура изображения сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения лежит на перпендикуляре, опущенном из центра О дуги на сопрягаемую прямую (рис.3, а), или на линии О1О2, соединяющей центры сопрягаемых дуг (рис.3, б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку сопряжения


Сопряжение двух пересекающихся прямых дугой заданного радиуса.
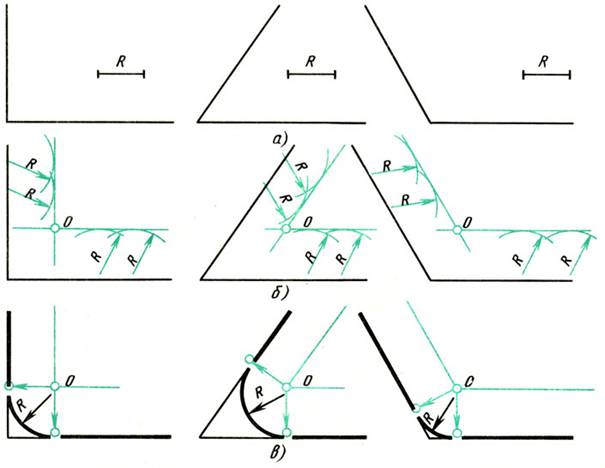
Даны пересекающиеся под прямым, острым и тупым углами прямые линии. Нужно построить сопряжения этих прямых дугой заданного радиуса R.
Для всех трех случаев применяют общий способ построения.
1. Находят точку О - центр сопряжения, который должен лежать на расстоянии R от сторон угла в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них.
Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.
2. Находят точки сопряжений. Для этого опускают перпендикуляры из точки О на заданные прямые.
3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рис.4, в).
Сопряжение двух параллельных прямых.
Заданы две параллельные прямые и на одной из них точка сопряжения т (рис.5, а). Требуется построить сопряжение.
|
|
|
Построение выполняют следующим образом:
1. Находят центр сопряжения и радиус дуги (рис.5, б). Для этого из точки m на одной прямой восставляют перпендикуляр до пересечения с другой прямой в точке п.
2. Из точки О - центра сопряжения радиусом Оm = Оn описывают дугу до точек сопряжения тип (рис.5, в).

Проведение касательной к окружности.
Задана окружность с центром О и точка А (рис.6, а). Требуется провести из точки А касательную к окружности.
1.Точку А соединяют прямой с заданным центром О окружности.
Строят вспомогательную окружность диаметром, равным ОА (рис. 6, а). Чтобы найти центр О1 делят отрезок ОА пополам.
2. Точки m и n пересечения вспомогательной окружности с заданной - искомые точки касания. Точку А соединяют прямой с точками m или n (рис.6, б). Прямая Am будет перпендикулярна к прямой Оm, так как угол АmО опирается на диаметр.

Сопряжение двух дуг окружности дугой заданного радиуса.
Заданы две дуги радиусами R1 и R2. Требуется построить сопряжение дугой, радиус которой задан.
Различают два случая касания: внешнее (рис.5, б) и внутреннее (рис.5, в). В обоих случаях центры сопряжений должны быгь расположены на расстоянии, равном радиусу дуги сопряжения, от заданных дуг. По общему правилу на прямых, соединяющих центры сопрягаемых дуг, находят точки сопряжения.
Ниже приведен порядок построения для внешнего и внутреннего касаний.
Для внешнего касания. 1. Из центров O1 и О2 раствором циркуля, равным сумме радиусов заданной и сопрягающей дуг, проводят вспомогательные дуги (рис.7, а); радиус дуги, проведенной из центра O1, равен R + R3, а радиус дуги, проведенной из центра O2, равен R2 + R3. На пересечении вспомогательных дуг расположен центр сопряжения - точка О3,.
2. Соединив прямыми точку O1 с точкой O3 и точку O2 с точкой O3, находят точки сопряжения m и n (рис.7, б),
|
|
|
3. Из точки О3 раствором циркуля, равным R3, между точками m и n описывают сопрягающую дугу.
Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов сопрягающей и заданной дуг, т.е. R4-R1 и R4-R2. Точки сопряжения р и k лежат на продолжении линий, соединяющих точку О4 с точками O1 и O2

Задания на выполнение сопряжений
Для гр.1712


Для гр. 1712



|
|
|


