 |
Задача о ранце (или рюкзаке)
|
|
|
|
ПОИС
Методические указания к практической работе.
Информационные системы и технологии в логистике. Часть 1. Программы оптимизации загрузки транспортных средств.
Теоретическая часть
Справочный материал:
Транспортная логистика
Транспортная логистика — это система по организации доставки, а именно по перемещению каких-либо материальных предметов, веществ и пр. из одной точки в другую по оптимальному маршруту. Одно из основополагающих направлений науки об управлении информационными и материальными потоками в процессе движения товаров.
Задачи, решаемые в транспортной логистике:
1. Выбор типа и вида транспортного средства.
2. Совместное планирование транспортных процессов со складскими и производственными операциями.
3. Совместное планирование транспортных процессов на различных видах транспорта.
4. Обеспечение технологического единства транспортно-складского процесса.
5. Определение рациональных маршрутов поставки.
Все эти задачи решаются взаимосвязано, в комплексе.
Оптимальная загрузка транспортных средств
Оптимальная загрузка транспортных средств одна из важнейших задач в логистике, эффективное решение которой не только позволяет уменьшить затраты на перевозку, но и сократить время погрузо-разгрузочных работ.
Существуют специальные Программы определения оптимального размещения груза в кузове автомобиля/контейнере/вагоне – Программы Оптимизации Загрузки Транспорта. “Данные Программы позволяют:
• сэкономить на перевозке, увеличив плотность загрузки на 5-20%;
• быстро ответить на вопрос о том сколько места займет груз в контейнере/полуприцепе/вагоне;
|
|
|
• не кладя трубки телефона рассчитать, какое кол-во груза нужно, чтобы заполнить весь объем транспорта;
• оптимально подобрать транспорт;
• точно определить, сколько понадобится контейнеров для большой отгрузки;
• быть абсолютно уверенным, что ничего не останется у поставщика.
Если Программа рассчитала, что поместится, значит поместится;
• заранее знать погонную длину груза в кузове при перевозке его как сборного;
• снизить количество боя при транспортировке;
• и т.д.
За короткое время, Программы перестали быть интересной игрушкой, а стали неотъемлемой частью программного обеспечения логистов. …
Компании с большими объемами отгрузок поспешили внедрить Программы в свои ERP-системы для еще более эффективной работы. Ведь по некоторым оценкам, снижение на 1% затрат в логистике предприятия эквивалентно увеличению продаж на 10-15%.
В условиях жесткой конкуренции и борьбе за выживаемость такие преимущества могут стать решающими.”[1] Из статьи Андрея Якимовича “Особенности национальной логистики или Почему в России до сих пор возят воздух?” (http://www.packer3d.ru/downloads/articles/national_logistic.pdf)
Задача о ранце (или рюкзаке)
Все программы оптимизации загрузки транспорта решают задачу известную в науке как “Задача о ранце” (англ. Knapsack problem) – это одна из задач комбинаторной оптимизации, существует много её разновидностей [2].
Пример формулировки “Задачи о ранце”: Общий вес ранца заранее ограничен. Какие предметы положить в ранец, чтобы общая полезность отобранных предметов была максимальна? Вес каждого предмета известен.
Математическая постановка задачи[3]
Пусть задано конечное множество предметов 
, для каждого 
известна ценность (стоимость) ci и определен обьем ai. Имеется рюкзак объема B. Требуется упаковать рюкзак так, чтобы общая ценность упакованных предметов была наибольшей, а их общий обьем не превосходил B. Традиционно полагают, что 
- целые неотрицательные числа.
|
|
|
Введем двоичные переменные 
:
xi = 1, если предмет 
выбран для упаковки,
xi = 0 в противном случае.
Тогда задача о рюкзаке сводится к следующей задаче линейного целочисленного программирования с булевыми переменными: найти такие значения переменных , при которых достигается максимум суммы
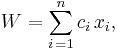(1)
и выполняется ограничение
(2)
Если имеется только одно ограничение вида (2), то задачу о рюкзаке называют одномерной, в противном случае - многомерной.
Неизвестно кто и когда первым привел формулировку данной задачи. Одно из первых упоминаний о ней встречается в статье Джорджа Балларда Мэтьюса 1897 г., основное же изучение “Задачи о ранце” началось во второй половине XX века. Несмотря на свою “древность” “Задача о ранце” не забывается и интерес к ней только возрастает, различные её модификации широко применяются в реальной жизни, на практике
- в криптографии,
- в логистике, для нахождения решения оптимальной загрузки различных транспортных средств: самолетов, кораблей, железнодорожных вагонов и т.д.
- при размещение грузов в складском помещении минимального объёма.
- при раскройке ткани — для заданного куска материала получить максимальное число выкроек определенной формы.
- в экономике – при расчете оптимальных капиталовложений и др.
|
|
|
