 |
Теория возмущений в приближении граничных МО
|
|
|
|
Квантово-химические правила отбора элементарных стадий
Любая термодинамически разрешенная реакция, в которой происходит незначительное перемещение ядер (близость минимумов энергетических термов) и мало изменяются электронные состояния (принцип наименьшего движения), и молекулярность которой не превышает 2, имеет шанс быть согласованным процессом, элементарной стадией. Однако, для того, чтобы величина 
была небольшой и реакция протекала с измеряемой скоростью, необходимо выполнение двух требований, вытекающих из квантово-химической теории. Эффективное взаимодействие двух частиц с достаточно низкой величиной барьера может происходить в случае, когда симметрия перекрывающихся молекулярных орбиталей (МО) будет одинаковой, а энергии этих МО будут близки. Например, бимолекулярная реакция (27)
H2 + I2 = 2HI (27)
с небольшим изменением координат ядер и валентных оболочек не является элементарным процессом (ЭС), поскольку запрещена по симметрии граничных МО. Рассмотрим подробнее некоторые квантово-химические подходы к проблеме реакционной способности.
Теория возмущений в приближении граничных МО
Из правила БЭП следует, что знание энергетического состояния исходных и конечных продуктов позволяет оценивать кинетические характеристики ЭС (вероятность реализации элементарного акта). Метод возмущения МО (МВМО), оперируя только граничными занятыми и свободными МО (ВЗМО, НСМО) и зарядами (на атомах в молекулах и на атомных орбиталях в МО) в исходных реагентах, позволяет в ряде случаев предсказать вероятность, направление и эффективность взаимодействия двух реагентов.
|
|
|
Чем эффективнее взаимодействие, тем ниже Еакт и тем выше вероятность согласованного (элементарного) акта.
Если энергии граничных орбиталей c 1 и c 2 близки, то энергия взаимодействия определяется резонансным (обменным) интегралом b 12
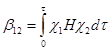(28)
где H – гамильтониан системы, t – элемент объема, в котором происходит перекрывание орбиталей. Величина b 12 в этом случае определяет и величину расщепления новых МО Y 1 и Y 2 или энергию стабилизации e = b 12.
Если энергии c 1 и c 2 различаются сильно, то величина e определяется не только b 12, а зависит и от разности энергий c 1 и c 2 по уравнению (29):
(29)
где Е 1 и Е 2 – энергии низшей и высшей МО
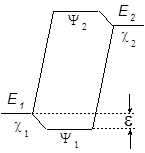
Чем больше величина e, тем стабильнее образующийся аддукт, тем ниже Еакт его образования.
МВМО не дает оценки Е переходного состояния и Еакт. Рассчитывается лишь разница между полной электронной энергией реагирующей системы Е и энергиями исходных реагентов 
и 
(малое возмущение):
D Е = Е – – , (30)
справедливое только для начальных участков координаты реакции. Только на больших расстояниях между реагентами не происходит смешения МО, нет межмолекулярного отталкивания и можно говорить о чистых МО исходных реагентов. Вместе с тем, такое приближение позволяет оценить наиболее вероятный путь реакции.
Энергию возмущения D Е при взаимодействии реагентов S и Т (S и Т – молекулы или активные центры в молекулах) рассчитывают по уравнению (31):
(31)
В случае только двух граничных МО (например, молекул донора и акцептора) уравнение упрощается (32):
(32)
|
|
|
В уравнениях (31, 32) qS и qT – эффективные заряды на центрах S и Т, RST – расстояние между центрами в ходе взаимодействия, e – диэлектрическая проницаемость среды. Таким образом, первый член (возмущение 1го порядка) отражает энергию кулоновского взаимодействия. Второй член (возмущение 2го порядка) определяет энергию орбитального перекрывания и включает: g ST – коэффициент, учитывающий заселенность электронами орбиталей c 1 и c 2, 
и 
– квадраты коэффициентов при атомных орбиталях центров S и Т волновой функции граничных МО c 1 и c 2, 
– квадрат обменного интеграла, Е 1 и Е 2 – энергии орбиталей c 1 и c 2. Разные случаи заселенности орбиталей c 1 и c 2 реагирующих частиц и коэффициент g ST приведены ниже:
| Число электронов на граничных орбиталях | g ST |
| 2 + 2, 0 + 0 | 0 (нет перекрывания) |
| 2 + 1, 1 + 0 | 1 |
| 2 + 0, 1 + 1 | 2 (самое сильное перекрывание) |
Если Е 1 – Е 2 в знаменателе уравнения (32) мало, заселенность g ST равна 1 и 2, симметрия орбиталей одинакова (b 12 > 0), геометрия орбиталей удобна для перекрывания (коэффициенты CS и CT имеют большие значения в одинаковых областях пространства) и второй член существенно больше первого, можно говорить об орбитально-контролируемой реакции.
Если Е 1 – Е 2 величина большая, второй член становится небольшим даже при больших CS и CT. Если при этом qS и qT также велики, говорят о зарядово-контролируемой реакции. Эти простые оценки полуэмпирическими методами МО ЛКАО позволяют определить (без расчетов ППЭ), в каком направлении (по каким центрам) пойдет та или другая реакция и можно ли ожидать высокой скорости от выбранной элементарной стадии. Естественно, что все соображения об оценке энергии D Е относятся только к элементарным стадиям.
Предположим, что донорная молекула, типичный нуклеофил SCN– реагирует с акцептором, имеющим НСМО. Если энергии ВЗМО донора (c 1) и НСМО акцептора (c 2) близки, реакция будет орбитально-контролируемой. Такая реакция будет протекать между молекулой акцептора и тем центром нуклеофила (донора), который обладает наивысшей плотностью заряда (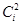
) на граничных орбиталях донора. Высшая занятая МО нуклеофила SCN– Y 2 имеет вид:
Y 2 = 0.74 j S + 0.33 j C – 0.59 j N
= 0.55 
= 0.35 >
Поэтому реакция с акцептором пойдет через атом S
|
|
|
(33)
Если орбиталь акцептора лежит высоко и Е 1 – Е 2 велика, реакция контролируется зарядовым взаимодействием. В этом случае, первый (кулоновский) член в уравнении (32) будет больше для того центра нуклеофила, у которого выше qi. Для расчета qS и qN необходимо учесть коэффициент 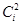при этих центрах на всех орбиталях, т.е. кроме y 2 нужно учесть и НЗМО y 1
y 1 = 0.33 j S + 0.59 j C + 0.74 j N
qi рассчитывается по уравнению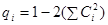 
qS = 1 – 2(0.332 + 0.742) = – 0.313
qN = 1 – 2(0.592 + 0.742) = – 0.7914
т.е. в анионе 
на атоме N эффективный отрицательный заряд выше | qN | > | qS | (заряд на атоме С, q С» 0.1). Таким образом, в условиях кулоновского контроля нуклеофил SCN– будет взаимодействовать с акцептором атомом азота
(34)
МВМО дал теоретическое объяснение ряду эмпирических правил и обобщений. В 1958 г Арланд, Чатт и Дэвис предложили классификацию комплексов металлов, разделив их на две группы (а) и (б). К группе (а) были отнесены ионы металлов (в наиболее распространенных степенях окисления), которые образуют наиболее устойчивые комплексы с лигандами, имеющими донорные атомы N, O, F. К группе (б) они отнесли ионы, образующие наиболее стабильные комплексы с лигандами, содержащими донорные атомы элементов третьего и последующих периодов (P, S, Cl, Br, J). Так, например, устойчивость галогенидных комплексов Zn2+ (группа (а)) и Hg2+ (группа (б)) меняется в следующих рядах:
Zn2+ F– >> Cl– > Br– > I–
Hg2+ I– > Br– > Cl– >> F–
При переходе к Hg2+ происходит обращение ряда устойчивости по сравнению с “обычным” рядом (Zn2+), согласующимся с простыми электростатическими представлениями.
Очевидно, что в случае первой группы ионов определяющим является зарядовый, а в случае второй группы ионов – орбитальный фактор. Аналогичные объяснения получили правило взаимодействия жестких и мягких кислот и оснований (Пирсон, 1963) и правило Корнблюма.
В терминах теории Пирсона взаимодействие жестких частиц (кислот и оснований, акцепторов и доноров) соответствует зарядовому контролю, взаимодействие мягких частиц – орбитальному контролю. Степень жесткости и мягкости акцептора (A) и донора (D) можно оценивать по различным критериям. Приведем величины орбитальных электроотрицательностей En (A) Em (D) (в эВ) по Клопману:
|
|
|
| Акцепторы: (кислоты) | Al3+ | Mg2+ | Cr3+ | Fe2+ | H+ | Na+ | Cu2+ | Zn2+ | Cu+ | Hg2+ | ||||||
| 6 | 2.42 | 2.06 | 0.69 | 0.42 | 0.0 | -0.55 | -1.0 | -2.3 | -4.6 | |||||||
|
|
|
|
|
|
|
|
| |||||||||
| Доноры: | F– | H2O | OH– | Br– | CN– | SH– | I– | H– | ||||||||
| -12.18 | -10.7 | -10.45 | -9.2 | -8.78 | -8.59 | -8.31 | -7.37 | |||||||||
В приведенной таблице самая жесткая кислота – Al3+, самое жесткое основание – F–. Самая мягкая кислота – Hg2+, самое мягкое основание – H–.
|
|
|
