Размещения, с повторениями

Размещением из n элементов по k с повторениями - кортежи, содержащая m элементов, взятых из данного множества, отличающихся либо элементами, либо их порядком следования, причем элементы в комбинациях могут повторяться от 1 до m раз.

Дано множество X={a,b,c,d}. составить все размещения из этого четыре элементного множества по два с повторениями. Эта записывается в виде: Ā _n^k.

Запишем некоторые кортежи длины 2. (a; a), (a; b). (a; c), (a; d), (b; b) …Всего таковых кортежей = 4·4=16. С другой стороны это есть численность декартового произведения =т(АхА)= 4·4=16

Запишем некоторые кортежи длины 3. (a; a; a), (a; a; b) …. Всего таковых кортежей = 4·4·4=64

Общая задача. Найти число кортежей дины k, которые можно составить из элементов множества, содержащего n элементов.

- число размещений с повторения из n элементов по k

Перестановки с повторениями

Необходимо составить шеренгу из 20 физкультурников, среди которых 10 имеют белые майки, 4- синие, 6 – красные. Сколькими способами это можно сделать? Если бы цвета не повторялись, то это можно сделать P(20)=20!. В виду того, что цвета будут повторяться, то перестановок с повторениями будет меньше в 10!·41·61· раз.

Общая задача. Имеются элементы k видов. Причем k₁ вида n₁ штук, k₂ вида n₂ штук и т.д. Сколько перестановок можно сделать из этих элементов?

, где n = n₁+n₂+…=n - сумма всех элементов.

Сочетания с повторениями

В магазине имеется вода жерех видов. Покупателю нужно приобрести 10 бутылок. Сколькими способами он это может сделать. По-другому, сколько различных наборов по 10 элементов можно составить из 4 наименований.

Составляемые наборы будут отличаться количеством элементов каждого наименования. Причем не обязательно, что бы присутствовали в таких наборах элементы всех наименований. Например, можно выбрать элементы только одного наименования или по несколько элементов каждого. В любом случае набор должен содержать установленное для данной ситуации число элементов, например 10 бутылок, как в рассматриваемой конкретной ситуации.

Ситуации такого характера приводят к сочетаниям с повторениями, Обозначается .

Общая задача. Требуется составить k наборов (кортежей) из элементов данных n множеств d₁. d₂, d₃,…d_n. Число элементов в каждом из множеств d_i не меньше числа k.

Формула вычисления числа сочетаний с повторениями имеет несколько разновидностей:

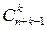= . = . =P(n-1;k).. Наиболее предпочтительнее первая формула, сведенная к вычислению сочетаний без повторения.

4. Примеры комбинаторных задач из различных областей знаний. Комбинаторика в древней Греции. Комбинаторика в биологии, генетике, химии и др.

В древне Греции философы, служители религии, астрологи, гадалки много внимания уделяли науке нумерологии – науке о числах. Они устанавливали различные закономерности числе, изучали влияние чисел и их комбинаций на человека, природу, мироздание.

Модель строения ДНК была расшифрована методами комбинаторики в 1953 году в Кембридже Ф.Криком и Дж. Уотсоном. Ими была изготовлена спиральная модель ДНК после рассмотрения различных комбинаций связи нуклеотидов, аминокислот и других объектов между собой. При этом был открыт генетический код, который содержит информацию о виде растения или животного, в том числе наследственную и иную информацию.

Без комбинаторных задач не было бы информатики, компьютера, сотового телефона. Например, установления кодов в ЭВМ для записи информации, такими, что бы они ни были избыточными и были достаточными для записи любой информации. Соединение элементов в ЭВМ, установление связей в кристалле, и микросхеме рассчитывается с помощью комбинаторных задач.

С точки зрения теории множеств, комбинаторика изучает подмножества конечных множеств, и операции над ними.

Приведем несколько общих таковых задач:

1.Найти конфигурацию элементов, обладающих заранее заданными свойствами.

2. Доказать существование или отсутствие конфигурации с заданным свойством.

3. Найти число конфигураций с заданным свойством

4. Описать все способы решения указанных выше задач.

5. Из всех возможных способов решения такой задачи выбрать наиболее оптимальную.

К перечисленным задачам подходят такие ситуации как:

1.Соеденить некоторое число точек на плоскости не пересекающими (пересекающими в одной, двух и более точках) линиями.

2. Транспортные задачи, связанные перевозками.

3. Задачи массового обслуживания

4.Определить число выпускаемых лотерейных биолитов, что бы были заинтересованы покупатели и авторы лотереи..

Практические замятия. Решение комбинаторных задач

Требования к знаниям умениям и навыкам Студент должен знать: основные комбинаторные объекты (типы выборок); формулы и правила количества выборок (для каждого из типов выборок) уметь: определять тип комбинаторного объекта (тип выборки); рассчитывать количество выборок заданного типа в заданных условиях.

 

Практические задания

1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра в запись числа входит только один раз?

2. Решение. Искомое число трехзначных чисел Р=3!=2-3 = 6.

3. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по два?

4. Решение. Искомое число сигналов М =6-5 = 30.

5. 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

6. Ответ: Искомое число способов С= 45.

7. 4. Их села N в село D ведет k дорог, а из села D в село Q ведет s дорог. Сколько существует различных способов поездки из села N в cело Q.

8. Имеется по 10 различных конвертов, открыток и марок. Сколькими способами можно составить комплект: конверт, марка, открытка?

9. Сколько необходимо издать словарей для перевода с одного языка на другой для 10 языков.

10.Из колоды в 36 карт составляется пара черная – красные масти. Сколькими способами это можно сделать.

11.Из колоды в 36 карт вытаскивается одна карта. Какова вероятность того, что вытащенная карта туз

12.Из колоды в 36 карт вытаскивается две карты подряд. Какова вероятность того, что первая ката будет дама, вторая – туз?

13.Брошены два игральных кубика. Найти вероятность того, что сумма выпавших очков четная.

Решение. Всего возможных вариантов равно 6·6=36. Благоприятствующие исходы наступят при выпадение следующих пар очков: 2-2, 2-4, 2-6, 4-2, 4-4, 4-6, 6-2, 6-4, 6-6. Всего получилось 9 таких вариантов. р=9/36=1/4=0,25

14.В группе 6 мужчин и 4 женщины. Наудачу отобрали 7 человек. Найти вероятность того, что среди отобранных лиц окажется 3 женщины.

Ответ: Р=(С₄³ · С₆⁴ ) / С₁₀⁷ =0,5

15.В группе спортсменов находится 7 человек перворазрядников и 3 второго разряда по шахматам. Наудачу отбирают поочередно троих человек Какова вероятность того, что все отобранные лица будут спортсмены первого разряда.

Ответ: Р= 7/10 · 6/9 · 5/8 = 7/24

16. Сколькими способами можно рассадить 5 человек на одной скамейке.

17.Сколькими способами можно выбрать из 20 человек 10 человек для участии в олимпиаде по информатике?

18.Сколько различных четырехзначных чисел можно составить из цифр 0,1,2,3,5,:6 если: цифры не повторяются, если цифры повторяются.

19.Сколькими различными способами можно выбрать несколько буква из фразы: "Око за око, зуб за зуб". Решение. Буква "о" входить 4 раза. Ее можно выбрать 4 раза или ни разу, потному для этой буквы существует 5 способов выбора. Аналогично для буквы "л" – 3 способа и т.д. 5·3·5·3·3·3=2025.

 

Дополнительные задания можно взять из [5, с 256] и [12, с 67]

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: