 |
Число размещений с повторением
|
|
|
|
Правило суммы
Если элемент А может быть выбран из данного множества n способами, и после этого элемент В может быть выбран m способами, то выбор элемента А или В может быть сделан (n+m) способами. (все понятия и формулы записываются, примеры подробно расписываются, совместно обсуждаем условие и находим решение, применяя изученные формулы,)
Пример 1:
Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение:
Данное множество – множество всех тем по алгебре и геометрии.
Обозначим: элемент А – выбранная тема по алгебре, В – выбранная тема по геометрии, т.е. выбрать тему по алгебре можно 17-ю способами 
n=17, а выбрать тему по геометрии – 13-ю способами m=13.
по правилу суммы: n+ m =17+13=30 тем.
Пример 2:
Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать
а) один билет из спортлото или автомотолотереи?
б) один билет из денежно-вещевой лотереи или автомотолотереи?
в) один билет из денежно-вещевой лотереи, спортлото или автомотолотереи?
Решение:
Обозначим:
Д-В – элемент А, n=5;
Сп. – элемент В, m=6;
Ав. – элемент С, k=10.
а) денежно-вещевая лотерея в выборе не участвует, то по правилу суммы m+ k = 6+10=16.
б) билеты спортлото в выборе не участвуют, тогда n + k = 5+10=15.
в) участвуют все билеты, т.е n + m + k=6+5+10=21.
Правило произведения
Если элемент A можно выбрать n способами из указанного множества, и после этого элемент B может быть выбран m способами, то выбор пары А и В может быть сделан (n 
m) способами.
Пример 3:
В книжном шкафу на двух полках стоят книги. На первой полке – 5 книг, а на второй – 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй?
|
|
|
Решение: Книгу с первой полки можно выбрать 5-ю способами, т.е. n=5, книгу со второй полки можно выбрать 10-ю способами, т.е. m=10. Для ответа на вопрос задачи воспользуемся правилом произведения.
5 10=50 способов.
Пример 4:
В лотерее каждому участнику даётся трёхзначный номер от 000 до 999. Организаторы лотереи решили, что выигрышными будут те номера, в которых есть хоть одна восьмерка. Сколько будет невыигрышных номеров?
Решение:
Первую цифру числа можно записать 9-ю способами, т.к. без восьмёрки n=9. Вторую и третью цифры числа можно также записать 9-ю способами m=9, k=9. Воспользуемся правилом произведения
m n k=9 9 9=729 проигрышных номеров.
Пример 5:
В букинистическом магазине лежат 6 разных изданий романа И.С. Тургенева «Рудин», три издания его же романа «Дворянское гнездо» и четыре издания романа «Отцы и дети». Кроме того, есть 5 разных сборников, в каждом из которых есть романы «Рудин» и «Дворянское гнездо», и 7 сборников с романами «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?
Решение:
Рудин – 6.
Дв. гнездо – 3
От. и дети – 4
- 5 изд
- 7 изд.
Воспользуемся правилами суммы и произведения:
6∙3∙4 + 5∙4 + 6∙7=72+20+42=134
Перед изучение следующей темы, повторим со школы теорию вероятности, ее формулы, повторим что такое факториал, как его находить и где применять. И так записываем следующую тему:
Упорядоченные и неупорядоченные выборки
Имеется множество, содержащее n элементов. Из этого множества выбрано m элементов.
Выбор может производиться с возвращением и без возвращения.
Выборки могут быть упорядоченными или неупорядоченными.
Выбор без возвращения.
1) В упорядоченных выборках важно, какие элементы их составляют, и в каком порядке они расположены. Упорядоченные выборки называются размещениями.
|
|
|
Число размещений из n по m – А 
А = 
(1)
Пример:
Сколько можно образовать различных четырехзначных чисел, чтобы цифры не повторялись?
(0,1,2,3,4,5,6,7,8,9)
n=10, m=4
Считаем число размещений, так как важен в каком порядке выбираются цифры:
2) Частным случаем размещений являются перестановки. Они содержат одинаковый набор элементов и отличаются лишь порядком этих элементов.
Число перестановок - 
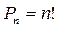(2)
Что такое факториал, кто помнит, как его можно расписать. Студент выходит к доске и расписывает, вместе с группой вспомнили и перешли к решению примеров.
Пример 6:
Сколько трехзначных чисел можно составить из цифр (1;6;8), чтобы цифры не повторялись?
Решение:
Считаем число перестановок, так как из 3х элементов выбираем 3:
3) Неупорядоченными называются выборки, в которых порядок расположения не важен, а важно лишь какие элементы составляют выборку. Неупорядоченные выборки называются сочетаниями.
Число сочетаний из n по m - 
(3)
или 
(4)
Пример 7:
В группе 10 человек. Нужно выбрать трех человек на одну и ту же должность. Сколько существует способов для выбора?
Решение:
Находим число сочетаний из 10 по 3(т.к. порядок не важен): 
способов.
Свойства сочетаний
ü 
, если n<k или k<0;
ü 
, 
;
ü 
;
ü Рекуррентная формула (выражает следующее через предыдущее)
, 
Задания записывают в тетрадь, затем далось 20 мин., для самостоятельной работы. Далее каждую задачу разобрали у доски до полного усвоения материала, студенты выходили к доске и объясняли какдый ход решения, что и от куда взяли и почему такой ответ.
Задания
1. Имеются 5 красок. Сколько существует способов для
а) выбора трех красок;
б) раскрашивания трехцветного полосатого флага с заданным направлением полос;
в) для раскрашивания трехцветного флага с заданным направлением полос, если одна полоса должна быть красной?
Решение:
а) Находим число сочетаний из 5 по 3 (т.к. порядок не важен)
способов.
б) Находим число размещений из 5 по 3 (т.к. важен порядок)
способов
в)
или 
или 
Находим в каждом случае число размещений из 4 цветов (т.к. пятый уже занят – красный) по 2 (т.к. цвет третьей полосы уже известен). А затем сложим их.
|
|
|
способов в каждом случае.
12+12+12=36 способов.
2. В группе 7 юношей и 5 девушек. Сколько существует способов для выбора 6 человек, чтобы среди них было не менее 4-х юношей.
Решение:
ю ю ю ю д д или
ю ю ю ю ю д или
ю ю ю ю ю ю
3. Среди 10 команд разыгрывается 3 комплекта медалей: золото, серебро, бронза. Сколько существует способов распределения?
Решение:
Находим число размещений из 10 по 3 (т.к. важен порядок):
Начало второй пары, знакомство с понятие Бином Ньютона.
Записывается формула с полным пояснением,.
Бином Ньютона
Выбор с возвращением
Число размещений с повторением
Имеется множество, содержащее n элементов, из которого берут k элементов, но с возвращением.(записывается в тетрадь, далее обсуждение совместное примера)
Пусть имеется множество элементов (a, b, c). Сколько можно образовать различных пар этих элементов (выбор с возвращением и порядок важен)?
(a,a), (a,b), (a,c)
(b,a), (b,b), (b,c) =>9 способов.
(c, a), (c, b), (c, c)
Знакомство с понятием перестановки с повторением. Разбор формул и наглядное применение их на примерах.
|
|
|
