Обусловленность задачи вычисления собственных значений.

Собственные значения и собственные векторы матрицы.

Методы решения проблемы собственных значений: степенной метод.

Пусть А — квадратная матрица порядка n.

Опр. Число называется собственным значением, аненулевойвектор — соответствующим собственным вектором матрицы А, если они связаны между собой соотношением .

Собственные значения матрицы и соответствующие им собственные векторы связаны соотношением , где Е — единичная матрица. Это означает, что собственный вектор — ненулевое решение однородной линейной системы . Решение этой однородной системы существует тогда и только тогда, когда . Следовательно, собственные значения матрицы могут быть вычислены как корни уравнения , а собственные векторы — как решения соответствующих однородных систем.

Опр. Уравнение называется характеристическим уравнением матрицы, а многочлен — характеристическим многочленом; характеристический многочлен матрицы порядка n является многочленом n -й степени относительно .

Мы уже знаем, что вычисление корней многочлена — плохо обусловленная задача. Следует искать такие методы вычисления собственных значений и собственных векторов матрицы, которые не требуют вычисления корней характеристического многочлена.

Для решения многих задач физики, механики, химии, биологии требуется знать все собственные значения и соответствующие собственные векторы. Эту задачу называют полной проблемой собственных значений. Однако в ряде случаев требуется найти только наибольшее, наименьшее по модулю собственное значение наиболее близкое к некоторому заданному числу и т.п. Такие задачи образуют частичную проблему собственных значений. Здесь будут рассмотрены только некоторые методы решения частичной проблемы собственных значений.

Обусловленность задачи вычисления собственных значений.

Опр. Матрица А называется симметричной, если А^т=А.

Пусть А — симметричная матрица, собственные значения которой и пусть А* — симметричная возмущенная матрица с собственными значениями .Собственные значения упорядочены по возрастанию. Доказано, что

,

Эти неравенства означают, что задача вычисления собственных значений симметричной матрицы хорошо обусловлена. Для несимметричных матриц дело обстоит совсем иначе. Для многих несимметричных матриц собственные значения чрезвычайно чувствительны к погрешностям элементов матрицы.

Пример плохо обусловленной задачи о собственных значениях несимметричной матрицы. Пример Дж. Уилкинсона. Рассмотрим верхнюю треугольную матрицу

.

Ее собственные значения — корни многочлена 20-й степени, который рассматривался в качестве примера плохо обусловленной задачи, т.е. . Если к элементу матрицы добавить малое возмущение 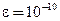, то характеристическое уравнение примет вид: , а собственные значения возмущенной матрицы окажутся полностью искаженными.

Здесь проблема обусловленности вычисления собственных значений несимметричной матрицы не обсуждается. Отметим лишь, что рассмотренное ранее число обусловленности матрицы системы линейных уравнений никак не связано с обусловленностью задачи о собственных значениях матрицы А.

Степенной метод вычисления наибольшего по модулю

собственного значения

Пусть требуется найти наибольшее по модулю собственное значение матрицы А, причем известно, что , 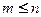; собственные значения матрицы предполагаются действительными, т.е. матрица А – симметричная. Если , то .Для несимметричных матриц возможно наличие комплексных корней с учетом кратности.

Простейший вариант степенного метода для вычисления : возьмем — произвольный начальный вектор, и построим последовательности векторов: и приближений по формулам: , ,

и при , причем .

Не приводя точных условий сходимости степенного метода, покажем механизм сходимости приближенных значений наибольшего по модулю собственного значения и при этом объясним название метода.

Пусть матрица А имеет базис из собственных векторов 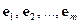. Выберем в качестве нулевого приближения собственного вектора такой вектор, в разложении которого по собственному базису коэффициент при отличен от нуля, , .

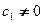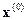Тогда , т.е. получается из умножением на к+ 1-ю степень матрицы А (отсюда и название метода).

,

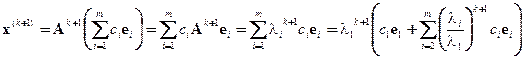а поскольку для i =2, 3, …, m, то 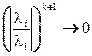при , и по формуле .Разделим и числитель, и знаменатель дроби на :

при .

Докажем оценку относительной погрешности: . Т.к.

. = (*)

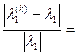
и т.к. положим , .

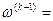
Так как для i =2, 3, …, m, то

Используя неравенство Коши-Буняковского ,имеем

. Тогда из равенства (*) и полученных оценок следует, что

. Что и требовалось докозать.

Однако, если , то при , а при , наоборот — . Для предупреждения таких случаев k- ю итерацию собственного вектора нормируют: , , , .

Заметим, что даже если первый коэффициент в разложении нулевого приближения по собственному базису окажется равным нулю, вследствие погрешностей округления он через несколько итераций станет ненулевым и итерации начнут сходиться.

Поделиться:

Воспользуйтесь поиском по сайту: