 |
Метод интегрирования подстановкой
|
|
|
|
Неопределённый интеграл.
Оглавление.
1. Понятие первообразной и неопределенного интеграла.
2. Свойства неопределенного интеграла.
3. Таблица основных неопределенных интегралов.
4. Метод интегрирования подстановкой.
5. Интегралы группы четырёх.
6. Интегрирование по частям.
7. Интегрирование рациональных дробей.
8. Интегрирование тригонометрических выражений.
9. Интегрирование иррациональных выражений.
Понятие первообразной и неопределенного интеграла.
В дифференциальном исчислении мы решали следующую основную задачу: по данной функции найти ее производную.
Многочисленные задачи науки и техники приводят к обратной задаче: для данной функции 
найти такую функцию 
, производная которой равнялась бы заданной функции , т.е.
Функция называется первообразной функцией для функции на интервале 
, если дифференцируема на и .
Аналогично можно определить понятие первообразной и на отрезке 
, но в точках 
и 
надо рассматривать односторонние производные.
Теорема. Если первообразная для функции на , то 
- также первообразная, где 
- любое постоянное число.
Доказательство. Имеем 
.
Определение. Произвольная первообразная для на называется неопределенным интегралом от функции и обозначается символом
Знак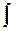 
называется интегралом, 
- подынтегральное выражение, - подынтегральная функция.
Если одна из первообразных для , то
Операцию нахождения неопределенного интеграла называют интегрированием функции . Она противоположна операции дифференцирования.
Примеры. Найти , если:
1. 
; 
; 
и т.д. В общем случае 
.
2. 
.
3. 
Функция имеет бесчисленное множество первообразных.
2. Свойства неопределённых интегралов.
|
|
|
1. 
2. 
3. 
4. 
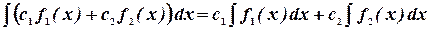
Доказательство. 
3. Таблица основных неопределенных интегралов.
1. 
2. 
5. 
6. 
7. 
8. 
Знание следующих интегралов облегчит решение многих задач.
9. 
10. 
11. 
12. 
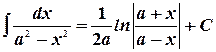
13. 
14. 
Отметим, что операция дифференцирования элементарных функций снова приводит к элементарным функциям. Операция интегрирования уже может привести к неэлементарным функциям, т.е. функциям, которые не выражаются через конечное число арифметических операций и суперпозицией элементарных функций.
Например, доказано, что следующие интегралы не интегрируются в элементарных функциях.
- интеграл Пуассона.
- интегралы Френеля.
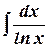- интегральный логарифм.
- интегральный косинус.
- интегральный синус.
Метод интегрирования подстановкой
Основную роль в интегральном исчислении играет формула замены переменных (или подстановки)
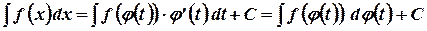
Пример.
Пример. 
.
Такого табличного интеграла нет. Сделаем замену - 
. Отсюда
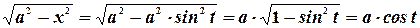
Перейдем от дифференциала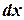 
к дифференциалу 
, для чего возьмем дифференциал от левой и правой частей формулы замены. Получим
.
Подставим в исходный интеграл:
И далее
Так как 
Но 
, поэтому
15. 
16. 
17. 
18. 
19. 
5. Интегралы группы четырёх.
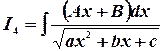
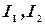
1) Разложим знаменатель, квадратный трехчлен:
2) Введем новую переменную 
3) Тогда знаменатель будет иметь вид:
Рассмотрим вначале случай, когда 
. При этом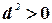 
. Следовательно
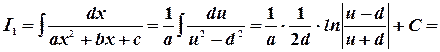
Или, возвращаясь к старым переменным
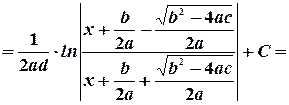
Преобразовывая, получим:
Теперь рассмотрим случай, когда 
. Квадратный трехчлен представим в виде:
Следовательно
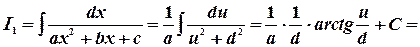
Опять возвращаясь к старым переменным, получим
Преобразовывая, найдем:
Рассмотрим теперь второй интеграл.
Или
Рассмотрим теперь третий интеграл. Используя разложение квадратного трехчлена, и, заменяя переменную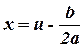 
, запишем:
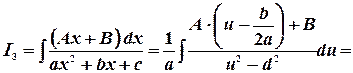
Полученное выражение представим в виде двух интегралов
|
|
|
В дифференциал первого интеграла внесем множитель 
Возьмем интегралы
Вернемся к старым переменным
Рассмотрим теперь последний интеграл 
. Аналогично, Используя разложение квадратного трехчлена, и, заменяя переменную 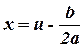, запишем
Полученное выражение также представим в виде двух интегралов
В первом интеграле под знак дифференциала введем , взяв второй интеграл и возвращаясь в нем к переменной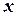 
, получим
Взяв первый интеграл, получим окончательно
6. Интегрирование по частям.
Известно, что дифференциал от произведения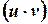 
равен:
Проинтегрируем полученное равенство
Интеграл от дифференциала некоторой функции равен самой функции:
Меняя местами слагаемые, получим:
Это и есть формула интегрирования по часям.
Пример. Вычислить интеграл 
.
Решение. Положим 
; 
.
Тогда
7. Интегрирование рациональных дробей.
Дробью называется выражение вида:
Дробь 
- правильная, если 
. Дробь - не правильная, если 
.
Простейшие дроби:
1. 
2. 
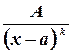
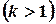
3. 
4. 
Интеграл от первой дроби - табличный интеграл:
1. 
Интеграл от второй дроби - также табличный:
2. 
3. Интеграл от третьей дроби см. интеграл группы четырёх.
4. Интеграл от четвертой дроби также см. интеграл группы четырёх.
Рассмотрим теперь дробь более общего вида.
Теорема. Пусть 
- правильная дробь, причем 
. Тогда эту дробь можно представить в виде:
Доказательство
Далее, выберем величину 
равной: 
. Тогда получим, что
И если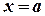 
, то
То есть является корнем многочлена 
. В этом случае многочлен можно представить в виде:
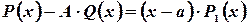
и, следовательно, далее запишем:
что и тр. док.
Следствие. Используя эту логику и дальше, можно записать:
Теорема.
Пусть 
- правильная дробь, причем 
. Тогда можно записать:
Следствие.
Таким образом, дроби общего вида сводятся к простейшим дробям.
8. Интегрирование тригонометрических выражений.
Для нахождения интегралов вида 
, где 
- рациональная функция, используют универсальную тригонометрическую подстановку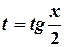 
.
Тогда 
.
То есть подынтегральная функция приобретает вид:
Пример. Взять интеграл 
. Введем новую переменную 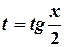. Тогда, как было показано выше 
и 
. Подставим эти значения в искомый интеграл:
Пример. Взять интеграл 
. Введем аналогичную замену переменных:
|
|
|
Частные случаи.
1. Интегралы вида
.
При этом делаем замену 
. Тогда
2. Интегралы вида 
,
где 
и 
натуральные числа.
Данные интегралы находятся с помощью тригонометрических формул 
, 
, 
, если и – четные.
Если хотя бы одно из чисел и - нечетное, то от нечетной степени отделяется множитель и вводится новая переменная:
При этом, если интеграл имеет вид 
,
то замена переменных: 
.
Если интеграл имеет вид 
то замена переменных: 
.
Пример. Взять интеграл 
. Замена переменных . Тогда
.
Наш интеграл примет вид:
Пример. Взять интеграл 
.
Преобразуем подынтегральное выражение:
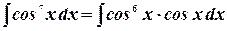
Косинус внесем под знак дифференциала, подынтегральную функцию преобразуем к следующему виду:
Возведем в куб подынтегральную функцию:
Сделаем замену переменных 
и проинтегрируем:
Вернемся к старой переменной:
Пример. Взять интеграл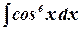 
.
Преобразуем подынтегральное выражение:
Возведем в куб:
Используем правило: интеграл от суммы равен сумме интегралов.
Сделаем преобразования под интегралами.
Возьмем уже "готовые" интегралы, а остальные преобразуем дальше
Сделаем дальнейшие преобразования
Взяв все интегралы, получим:
Перегруппировывая, получим:
Пример. Взять интеграл 
.
Преобразуем подынтегральное выражение
В первом интеграле учтем, что 
Во втором интеграле учтем, что 
Интеграл от суммы равен сумме интегралов
Учтем еще раз, что
Интеграл от суммы равен сумме интегралов
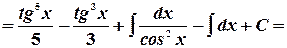
Далее
Окончательно
.
Используя известное тригонометрическое тождество
можно упростить взятие некоторых интегралов.
Пример.
|
|
|
