 |
Функции нескольких переменных
|
|
|
|
Понятие дифференциала
Пусть функция y = f (x) дифференцируема при некотором значении переменной x. Следовательно, в точке x существует конечная производная
Тогда по определению предела функции разность
(1)
является бесконечно малой величиной при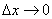 
. Выразив из равенства (1) приращение функции, получим
(2)
(величина 
не зависит от 
, т. е. остаётся постоянной при ).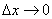
Если 
, то в правой части равенства (2) первое слагаемое 
линейно относительно . Поэтому при
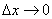
оно является бесконечно малой того же порядка малости, что и . Второе слагаемое 
- бесконечно малая более высокого порядка малости, чем первое, так как их отношение 
стремится к нулю при
Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
(3)
Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают
или
Следовательно,
(4)
или
(5)
Итак, дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента,
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (5) это видно из записи, в формуле (4) – нет.
Дифференциал функции можно записать в другой форме:
(6)
или
Геометрический смысл дифференциала. Дифференциал функции y = f (x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении x на величину 
.
|
|
|
Дифференциалы высших порядков
Напомним, что дифференциал функции 
(называемый также первым дифференциалом, или дифференциалом первого порядка) задаётся формулой
Рассмотрим это выражение (при фиксированном приращении 
аргумента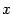 
) как функцию переменного 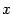и найдём её дифференциал 
:
Этот дифференциал от первого дифференциала называется вторым дифференциалом от функции , или дифференциалом второго порядка. Аналогично, дифференциал от второго дифференциала называется третьим дифференциалом; он задаётся формулой
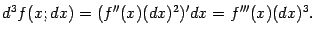
Вообще, 
-й дифференциал 
, или дифференциал -го порядка, определяется как дифференциал от 
-го дифференциала (при постоянном приращении ); для него имеет место формула:
При 
-й дифференциал не инвариантен (в отличие от первого дифференциала), то есть выражение 
зависит, вообще говоря, от того, рассматривается ли переменная 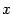как независимая, либо как некоторая промежуточная функция другого переменного, например, 
.
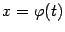Для доказательства неинвариантности дифференциалов высших порядков достаточно привести пример. Пусть 
и 
. Если 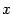-- независимая переменная, то
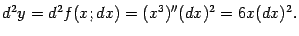
| (4.16) |
Если же 
, то 
, и тогда правая часть формулы (4.16) даёт:
Однако при этом 
и
Как видно, получилось не то же самое, что по формуле (4.16) с учётом зависимости 
. Следовательно, уже второй дифференциал не обладает свойством инвариантности при замене переменной. Тем более, не инвариантны дифференциалы порядков 3 и выше.
Функции нескольких переменных
1. Определение. Если каждой паре (x, y) значений двух независимых переменных из области Wставится определенное значение z, то говорят, что z есть функция двух переменных (x, y).
|
2. Геометрическое изображение функции двух переменных - поверхность.
3. Частное и полное приращение функции.
Полное приращение функции
|
Частное приращение функции
|
|
|
|
|
Вообще, полное приращение функции не равно сумме частных приращений.
Пример. z = xy.
|
|
|
4. Непрерывность функции нескольких переменных
Предел функции.
Пусть z = f (x, y) определена в некоторой окрестности A (x 0, y 0).
Определение. Постоянное число b называют пределом z = f (x, y) при P (x, y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству | AP | < d, имеет место неравенство | f (x, y)- b | < e.
5. Непрерывная функция
6. Частные производные
|
|
|
