Задание по теории графов №4

Задание по комбинаторике

Куб окрашивается 7 цветами. Определить число различных комбинаций окрашивания куба, если все стороны куба считаются различными:

1) если допускается окрашивать грани куба в один и тот же цвет;

2) каждая грань окрашивается различными цветами;

 

Решение: У куба 6 граней. все стороны куба считаются различными (например, нумерованными). Значит комбинация состоит из 6 элементов.

1) если допускается окрашивать грани куба в один и тот же цвет;

 

Так как все грани куба различны, то порядок важен. Цвета могут повторяться. Речь идет о размещениях с повторениями 6 элементов из 7.

Формула подсчета числа размещений с повторениями:

2) каждая грань окрашивается различными цветами;

Так как все грани куба различны, то порядок важен. Цвета не могут повторяться. Речь идет о размещениях без повторений 6 элементов из 7.

Формула подсчета числа размещений с повторениями:

 

6. Задание по теории графов №1 (по вариантам)

 

По данной матрице смежности постройте ориентированный граф и, если это возможно, неориентированный граф. Определите степени и полустепени вершин.

 

 

Поскольку данная матрица является матрицей третьего порядка с, то ей соответствует ориентированный граф с тремя вершинами.

Элемент а₁₁ матрицы равен нулю. Это означает, что у дуги, начало и конец которой в вершине Х₁ (петли) не существует. Элемент а₁₂= 1, вершины Х₁, и Х₂ соединены одной дугой, начало которой в Х₁, конец в Х₂. а₁₃=3, поэтому вершина Х₁ инцидентна трем дугам, исходящим из Х₁ и заходящим в Х₃. Элемент а₂₁= 1, вершины Х₂, и Х₁ соединены одной дугой, начало которой в Х₂, конец в Х₁. И так далее.

 

 

Полустепени исхода d^-(X₁)=4, d^-(X₂)=3, d^-(X₁)=5.

Полустепени захода d⁺(X₁)=4, d⁺(X₂)=3, d⁺(X₁)=5.

 

Поскольку данная матрица является симметричной матрицей третьего порядка с неотрицательными элементами, то ей соответствует неориентированный граф с тремя вершинами. Расположив вершины Х₁, Х₂, Х₃ на плоскости произвольным образом, соединяем их с учетом кратности ребер. Так как а₁₁= 0, то ребер начала и концы которых совпадают с этой вершиной Х₁ (петли), не существует. Элемент а₁₂= 1, вершины Х₁, и Х₂ соединены одним ребром. а₁₃=3, поэтому вершина Х₁ инцидентна трем ребрам, соединяющим Х₁ и Х₃. И так далее.

 

 

 

 

Степени вершин d(X₁)=4, d(X₂)=3, d(X₁)=5

Задание по теории графов №2

По данной матрице инцидентности постройте граф. Определите степени (полустепени) вершин.

 

 

;

 

 

Степени вершин d(X₁)=2, d(X₂)=3, d(X₁)=2, d(X₄)=3.

 

Задание по теории графов №3

 

Укажите, если он существует, изоморфизм следующих графов

 

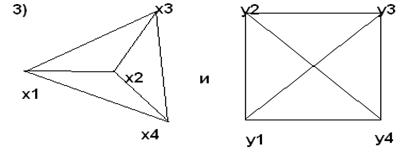
Графы изоморфны тогда и только тогда, когда их матрицы смежностей получаются друг из друга одинаковыми перестановками строк и столбцов.

Матрица смежности 1 го графа

Матрица смежности 2 го графа

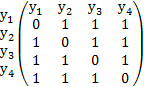
Мы видим. что матрицы смежности совпали. Значит между графами можно установить взаимно однозначное соответствие, графы –изоморфны.

 

Задание по теории графов №4

Определите, являются ли следующие графы эйлеровыми. Если да, то укажите эйлеров цикл.

 

 

Решение:

Теорема (Эйлер). Для того чтобы данный связный граф был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными. Связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными.

 

В данном случае степени вершин Х₂, Х₃, Х₄, Х₆, Х₇, Х₈ – четные, а степени Х₁, Х₅, Х₉, Х₁₀ – нечетные. Данный граф не является ни эйлеровым, ни полуэйлеровым.

 

 

 

 

Решение:

1. Сначала выразим число в алгебраическом виде z=a+i*b/

Для этого умножим знаменатель на сопряженный множитель ( получим

2. Находим тригонометрическую форму комплексного числа z =
Модуль комплексного числа |z|.

Поскольку a > 0, b > 0, то arg(z) находим как:

 

arg(z)=φ=arctg()

 

φ=arctg()= arctg()

Таким образом, тригонометрическая форма комплексного числа

 

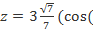arctg())+i*sin arctg()))

 

3. Находим показательную форму комплексного числа

 

z=|z|e^iφ=

 

Поделиться:

Воспользуйтесь поиском по сайту: