преобразованием переменных.

Ортогональные матрицы.

Определение 1. Вещественную квадратную матрицу будем называть ортогональной, если обратная к ней матрица равна транспонированной, т.е. ( - ортогональная) , или

( - ортогональная)

Пример 1. Пусть . Подсчитаем произведение

. Следовательно, - ортогональная матрица.

Определение 2. Вещественный столбец будем называть нормированным, если сумма квадратов его элементов равна единице, т.е. если .

Вещественную строку будем называть нормированной, если сумма квадратов её элементов равна единице, т.е. если .

 

Пример 2. Столбец - нормированный, т.к. .

Строка - нормированная, т.к. .

 

Лемма 1. Для того чтобы вещественная квадратная матрица была ортогональной, необходимо и достаточно, чтобы её столбцы были попарно ортогональны и нормированы.

Для того чтобы вещественная квадратная матрица была ортогональной, необходимо и достаточно, чтобы её строки были попарно ортогональны и нормированы.

 

Доказательство проведём для столбцов. Доказательство для строк совершенно аналогичное предлагается провести самостоятельно.

Пусть (R), где R для .

Тогда , т.е. .

Из определения 1 следует, что утверждение - ортогональная матрица означает, что , т.е.

для всех . Если , то это означает, что . Следовательно, столбцы матрицы нормированы. Если 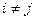, то это равносильно тому, что . Следовательно, столбцы матрицы попарно ортогональны. Это рассуждение можно записать с помощью символов:

( - ортогональная)

.

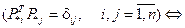
Лемма доказана.

 

Свойства ортогональных матриц.

1. Матрица, обратная к ортогональной, также ортогональная.

Доказательство. ( - ортогональная)

-ортогональная).

Здесь мы воспользовались одним из свойств операции транспонирования для обратимых матриц: .

 

2. Произведение ортогональных матриц одного порядка также является ортогональной матрицей.

Доказательство. Пусть - ортогональные матрицы одного порядка, т.е. .

Найдём матрицу, обратную к матрице : .

Таким образом, 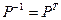, и - ортогональная матрица.

 

3. Единичная матрица - ортогональная, т.к. .

 

4. Определитель ортогональной матрицы равен .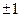

Доказательство. Пусть - ортогональная матрица. Тогда . Следовательно, . Здесь мы воспользовались 1-ым свойством определителя: .

 

Приведение вещественной квадратичной формы к каноническому виду ортогональным

преобразованием переменных.

 

Теорема 1. Любая вещественная квадратичная форма может быть приведена к каноническому виду линейным преобразованием переменных с ортогональной матрицей, т.е. если , где (R), то существует такая ортогональная матрица 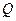, что .

Теорема приводится без доказательства.

Следствие. Для того чтобы линейное преобразование переменных 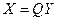с ортогональной матрицей

приводило вещественную квадратичную форму с матрицей к каноническому виду , необходимо и достаточно, чтобы совокупность чисел 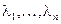была бы спектром матрицы , а столбцы матрицы 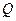были бы собственными векторами этой матрицы, принадлежащими собственным числам 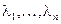соответственно.

Доказательство. Очевидно:

Последнее равенство означает, что столбец является собственным столбцом матрицы , соответствующим собственному числу , .

 

Пример 1. Приведём вещественную квадратичную форму к каноническому виду линейным преобразованием переменных с ортогональной матрицей.

Выпишем матрицу этой квадратичной формы: .

Характеристический многочлен этой матрицы был вычислен в §5.

Найдём собственные векторы матрицы . В §5 было показано, что любой собственный вектор этой матрицы, соответствующий собственному числу имеет вид: , где ; любой собственный вектор этой матрицы, соответствующий собственному числу имеет вид: , где .

Построим ортогональную матрицу , состоящую из собственных векторов матрицы .

Положив , получаем столбец . Умножим этот столбец на число так, чтобы получившийся столбец был бы нормированным. Для этого подсчитаем число . Тогда . Положим . Столбец является собственным вектором матрицы , соответствующим собственному числу , т.к. он получается из столбца , при , и он нормированный.

Теперь найдём собственные векторы матрицы , соответствующие собственному числу .

Возьмём 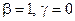. Получившийся в результате столбец 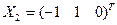является собственным вектором матрицы , соответствующим собственному числу . Ещё один собственный вектор , соответствующий собственному числу , будем искать так, чтобы он был ортогонален столбцу , т.е. чтобы . Положим . Тогда . Нормируем эти столбцы. Для этого подсчитаем числа . Положим . Столбцы и являются собственными векторами матрицы , соответствующим собственному числу по лемме § 5 и они нормированные. Столбцы попарно ортогональны и нормированы. Следовательно, по лемме §6 матрица является ортогональной, а её столбцы – собственные векторы матрицы . Из следствия к теореме этого параграфа получаем: , или . Убедимся в справедливости последнего равенства непосредственным вычислением: или дствия к теореме этого параграфа получаем:о, по лемме

Пример 2. Привести к каноническому виду и определить тип поверхности, уравнение которой имеет вид: (1)

Выделим в левой части уравнения квадратичную форму и приведём её к каноническому виду ортогональным преобразованием переменных. Это было сделано в примере 1: (2)

Выясним геометрический смысл линейного преобразования переменных .

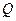Исходное уравнение (1) поверхности задано в правой декартовой прямоугольной системе координат . Напомним, что точка - начало координат, а - правый ортонормированный базис. Рассмотрим новую декартову прямоугольную систему координат , в которой базис получается из базиса следующим образом: , т.е. матрица является матрицей перехода от базиса к базису . Таким образом, . Заметим, что базис также правый, т.к. легко подсчитать определитель матрицы 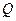, который равен 1. Напомним, что

 

Следовательно, и базис - правый ортонормированный.

Изобразим на каждом рисунке в отдельности векторы нового базиса:

Подставим в уравнение (1) вместо и их выражения через и из формул (2). В результате получим уравнение поверхности в системе координат :

.

Теперь выделим полные квадраты при и :

Введём новую систему координат , которая получается из предыдущей в результате параллельного переноса. Координаты точки в новой и в предыдущей системах координат связаны соотношениями:

.

Изобразим на рисунке эти две системы координат:

Таким образом, в новой системе координат уравнение поверхности имеет вид:

.

Следовательно, эта поверхность эллипсоид, т.к. мы получили каноническое уравнение эллипсоида.

Новая система координат является канонической для этой поверхности. На следующем рисунке эта поверхность изображена в канонической системе координат.

 

 

 

Поделиться:

Воспользуйтесь поиском по сайту: