 |
Задания для самостоятельной работы
|
|
|
|
Порядок выполнения
1. Упражнения выполняются параллельно с изучением теоретического материала.
2. После выполнения каждого упражнения результаты заносятся в отчёт.
3. При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, то проконсультироваться с преподавателем.
4. Дома доделать упражнения из раздела «Краткие теоретические сведения и практические упражнения», которые Вы не успели выполнить во время аудиторного занятия.
5. После выполнения упражнений выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы и (см. ниже).
6. Подготовить отчёт, в который включитьупражнения из раздела «Краткие теоретические сведения и практические упражнения» и упражнения для самостоятельной работы. Отчёт представить в виде документа Microsoft Word, имя файла (пример): mp_10_Ivanov_P_01_s_1 (факультет_группа_Фамилия студента_Инициал_номер лабораторной, семестр). Отчет должен содержать по каждому выполненному упражнению: № упражнения, текст упражнения; команды, скопированные из командного окна, с комментариями к ним и результаты их выполнения, включая построенные графики; тексты М-сценариев и М-функций; выводы.
Краткие теоретические сведения
И практические упражнения
1. Символьное вычисление неопределённого интеграла. Неопределённые интегралы от символических функций вычисляются с помощью int, входными аргументами указываются символическая функция и переменная, по которой ведётся интегрирование.
Пример 1.
>> syms x; f=sym('x^3*exp(x)'); I=int(f,x)
|
|
|
I =
x^3*exp(x)-3*x^2*exp(x)+6*x*exp(x)-6*exp(x)
>> pretty(I)
Упражнение 1. Вычислить неопределённые интегралы:
а)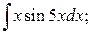 
б) 
.
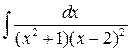2. Символьное вычисление определённого интеграла. При вычислении определённого интеграла в символьном виде следует задать значения нижнего и верхнего предела в качестве нижнего и верхнего предела в int.
Упражнение 2. Вычислить определённые интегралы в символьном виде:
а) 
; б)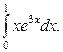 
Интегральные суммы и суммы Дарбу.
Упражнение 3. Создать М-функции, вычисляющие значения интегральных сумм на отрезке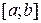 
при равномерном разбиении его на 
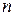отрезков и выбором точек на:
а) левых концах отрезков разбиения;
б) правых концах отрезков разбиения.
Проверить работу М-функций, сопоставив результат выполнения программы и результат, полученный вручную, для интегральных сумм функции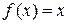 
на отрезке 
при разбиении его на четыре равных части.
Упражнение 4. Создать М-функции, вычисляющие значения верхних и нижних сумм Дарбу на отрезке 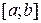при равномерном разбиении его на 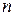отрезков. Проверить работу М-функций, сопоставив результат выполнения программы и результат, полученный вручную, для сумм Дарбу функции 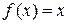на отрезке при разбиении его на четыре равных части.
Упражнение 5. Используя M-функции упр. 3 и 4, вычислить интегральные суммы и суммы Дарбу для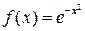 
на отрезке при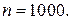 
4. Численное интегрирование. Функция quad(‘f’,a,b) вычисляет значения определенного интеграла функции f на отрезке 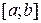с точностью до 
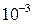по формуле Симпсона. Для повышения точности вычислений следует задать дополнительный четвёртый аргумент – требуемое значение точности.
Упражнение 6. Вычислить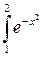 
, используя функцию quad. Сравнить результат с результатами упражнения 5, вычислив разности между численным значением интеграла, полученным по формуле Симпсона, и значениями интегральных сумм и сумм Дарбу.
Задания для самостоятельной работы
1. Выполнить упражнения из раздела «Краткие теоретические сведения и практические упражнения», которые не успели сделать в аудитории.
|
|
|
2. Ответить на контрольные вопросы:
1) Почему при символьном вычислении неопределенного интеграла от функции с действительной областью определения и действительным множеством значений результат может содержать комплексные числа?
2) Что представляет собой с геометрической точки зрения интегральная сумма?, нижняя сумма Дарбу?, верхняя сумма Дарбу?
3) Предположим, что нам неизвестно аналитическое задание функции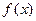 
, но известно, что 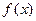непрерывна на 
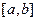, и известны наименьшие и наибольшие значения 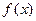на каждом из 100 отрезков равномерного разбиения отрезка 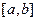. Как нам оценить значения 
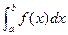? Можем мы ли мы найти приближенное значение интеграла с помощью функции quad?
3. Самостоятельно выполнить упражнения:
Упражнение С1. Вычислить интеграл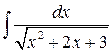 
:
а) используя средства MatLab;
б) без использования MatLab.
Сопоставить и объяснить результаты.
Упражнение 2С. Вычислить определённый интеграл 
, используя символьное вычисление MatLab.
Упражнение 3С. Создать М-функцию, вычисляющую значения интегральных сумм на отрезке 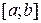при равномерном разбиении его на 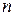отрезков и выбором точек, делящих отрезки разбиения в произвольном заданном отношении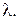 
Проверить работу М-функции, сопоставив результат выполнения программы и результат, полученный вручную, для интегральных сумм функции 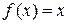на отрезке при разбиении его на четыре равных части и выбором точек, делящих отрезки разбиения пополам.
Список рекомендуемой литературы
1. В.Г.Потемкин "Введение в Matlab" (v 5.3), http://matlab.exponenta.ru/ml/book1/index.php - 3.1
2. Сборник задач по математике для втузов под ред. А.В.Ефимова и А.С.Поспелова, часть 2, М.2002, - 5.5.
3. А. Кривелёв. Основы компьютерной математики с использованием системы MatLab. М, 2005. – 6.1..
|
|
|
