 |
Графики функций двух переменных.
|
|
|
|
Порядок выполнения
1. Упражнения выполняются параллельно с изучением теоретического материала.
2. После выполнения каждого упражнения результаты заносятся в отчёт.
3. При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, то проконсультироваться с преподавателем.
4. Дома доделать упражнения из раздела «Краткие теоретические сведения и практические упражнения», которые Вы не успели выполнить во время аудиторного занятия.
5. После выполнения упражнений выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы и (см. ниже).
6. Подготовить отчёт, в который включитьупражнения из раздела «Краткие теоретические сведения и практические упражнения» и упражнения для самостоятельной работы. Отчёт представить в виде документа Microsoft Word, имя файла (пример): mp_10_Ivanov_P_01_s_1 (факультет_группа_Фамилия студента_Инициал_номер лабораторной, семестр). Отчет должен содержать по каждому выполненному упражнению: № упражнения, текст упражнения; команды, скопированные из командного окна, с комментариями к ним и результаты их выполнения, включая построенные графики; тексты М-сценариев и М-функций; выводы.
Краткие теоретические сведения
И практические упражнения
Функции многих переменных. Область определения.
Упражнение 1. Создать М-функции, строящие графики функций 
на промежутке 
(
при 
) и показывающую вертикальной штриховкой область, заключенную между графиками. Входные аргументы – функции, границы отрезка и количество отрезков, на которые разбивается отрезок:
|
|
|
а) верхняя и нижняя границы сплошные, б) обе границы пунктирные;
в), г) одна граница сплошная, другая пунктирная.
Упражнение2. Используя М-функции из упр. 1, построить области определения функции 
.
Графики функций двух переменных.
Для отображения функции двух переменных следует:
1. Сгенерировать матрицы для отображения узлов сетки на прямоугольной области определения функции.
2. Вычислить функцию в узлах сетки и записать полученные значения в матрицу.
3. Использовать одну из графических функций MatLab.
4. Нанести на график дополнительную информацию, в частности, соответствие цветов значениям функции.
Сетка генерируется с помощью команды meshgrid, вызываемой с двумя аргументами. Аргументами являются векторы, элементы которых соответствуют сетке на прямоугольной области построения функции. Можно использовать один аргумент, если область построения функции квадрат.
Пример 1. Сгенерируем сеткуна области 
и значения в узлах для функции 
>> [X, Y]=meshgrid(-1:0.05:1, 0:0.05:1);
>>Z=4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);
Для построения каркасной поверхности используется функции mesh, вызываемая с тремя аргументами:
>> mesh(X,Y,Z)
Цвет линий поверхности соответствует значениям функции. MatLab рисует только видимую часть поверхности. С помощью команды hidden off можно сделать каркасную поверхность «прозрачной», добавив скрытую часть. Команда hidden on убирает невидимую часть, возвращая графику прежний вид.
Функция surf строит каркасную поверхность графика функции и заливает каждую клетку поверхности определённым цветом, зависящим от значения функции в точках, соответствующим углам сетки, в пределах каждой клетки цвета постоянны:
>> surf(X,Y,Z)
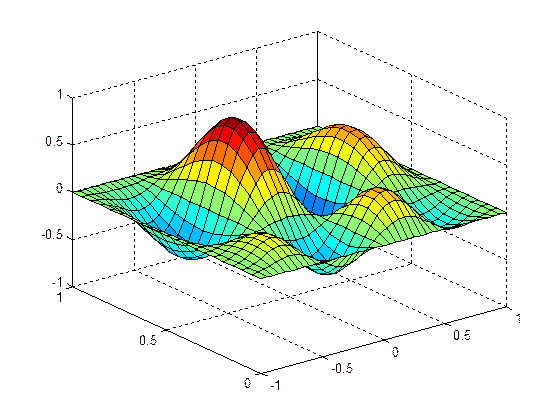
Команда shading flat позволяет убрать каркасные линии:
Для получения поверхности, плавно залитой цветом, предназначена команда shading interp. При помощи команды shading faceted можно вернуться к изображению каркасной поверхности, залитой цветом.
|
|
|
В MatLab определена команда colorbar, которая выводит рядом с графиком функции столбик, устанавливающий соответствие между цветом и значением функции:
>> surf(X,Y,Z)
>> colorbar
Команду colorbar можно применять в сочетании со всеми функциями, строящими трёхмерные объекты.
Упражнение3. Построить каркасную поверхность, залитую цветом, с указанием соответствия цветов значениям для функции 
.
3. Линии уровня. Пользуясьужерассмотренными графиками, трудно сделать вывод о значении функции в той или иной точке плоскости 
Команды meshc и surfc позволяют получить более точное представление о поведении функции. Эти команды строят каркасную поверхность или залитую цветом каркасную поверхность и размещают на плоскости 
линии уровня функции (линии постоянства значений функции):
>> surfc(X,Y,Z)
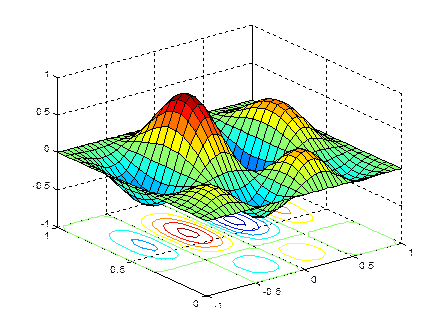
MatLab позволяет построить поверхность, состоящую из линий уровня при помощи функции countour3. Эту функции. Можно использовать с тремя аргументами countour3(X,Y,Z). При этом число линий уровня выбирается автоматически. Имеется возможность задать четвёртым аргументом в countour3 либо число линий уровня либо вектор, элементы которого равны значениям функции, отображаемым в виде линий уровня:
>> levels=[0:0.01:0.5]
>>contour3(X,Y,Z,levels)
Упражнение 4. Для функции из упражнения 3 построить линии уровня и поверхности, состоящие из линий уровня.
4. Контурная графика. Более содержательную информацию о числовых значениях функции дают плоские контурные графики, содержащие линии уровня исследуемых функций. Использование countour с тремя аргументами приводит к графику, на котором показываются линии уровня на плоскости:
>> contour(X,Y,Z)
Каждую линию уровня функции можно снабдить значением, которое принимает на ней исследуемая функция, при помощи функции clabel. Функция contour, вызываемая с двумя выходными параметрами, не только строит линии уровня, но и автоматически находит требуемые для clabel параметры. В массиве CMatr содержится информация о линиях уровня, а в массиве h – указатели. Желательно завершить вызов CMatr точкой с запятой для подавления вывода на экран значений выходных параметров.
>> [CMatr,h]=contour(X,Y,Z);
>> clabel(CMatr,h)
|
|
|
>> grid on
Дополнительным аргументом функции contour может быть или число линий уровня или вектор, содержащий значения функции, для которых требуется построить линии уровня.
Упражнение5. Для функции из упр. 3 построить плоские линии уровня без нанесения и с нанесением значений функции с шагом 0.1. Нанести сетку.
Наглядную информацию об изменении функции даёт заливка прямоугольника на плоскости 
цветом, зависящим от значений функции в точках плоскости. Для построения таких графиков предназначена функция contourf, использование которой не отличается от использования contour:
>> contourf(X,Y,Z,20)
>> colorbar
Упражнение6. Для функции из упр. 3 построить плоские линии уровня для 10 значений функции с заливкой промежутков между линиями уровня и шкалой соответствия цветов значениям функции.
|
|
|
