 |
Свободное движение. Общее решение уравнения Шредингера.
|
|
|
|
Московский институт электронной техники
Кафедра КФН
Лабораторная работа 2
Свободное движение электрона. Волновой пакет.
Общие указания.
На экране моделируется движение электрона в виде изменяющегося со временем распределения плотности вероятности. Кривая на экране имеет вид гауссовой кривой. Эта кривая описывает распределение плотности вероятности 
, для электрона в состоянии с волновой функцией 
. Обычно эту волновую функцию называют волновым пакетом. Однако для простоты будем называть волновым пакетом распределение плотности вероятности 
.
Движение волнового пакета характеризуется тремя физическими параметрами.
1. Амплитуда волнового пакета 
– это максимальное значение распределения плотности вероятности. По мере движения электрона, амплитуда пакета уменьшается.
2. Полуширина пакета 
– это половина ширины распределения плотности вероятности на высоте в e раз меньшей амплитуды пакета. По мере движения электрона, амплитуда пакета уменьшается.
3. Скорость движения электрона 
– это скорость движения вершины пакета. По мере движения электрона, скорость не меняется.
Скорость электрона вычисляется с помощью следующей формулы.
. (1)
Здесь 
– импульс электрона, m - масса электрона. В приложении доказывается, что есть среднее значение электрона в состоянии с волновой функцией . Соответственно является средней скоростью электрона в этом состоянии . Среднее значение импульса удобно связать с энергией 
с помощью формулы.
. (2)
Задается энергия электрона , в электрон-вольтах 
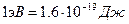. Энергию будем менять в пределах 0 ¸ 1000 эВ. Необходимо поэкспериментировать с разными значениями энергии. Если взять небольшую энергию, например 1 эВ, то пакет движется медленно, быстро деформируется на небольших расстояниях. Если же взять большую энергию, например 1000 эВ, то волновой пакет проходит всю рабочую область экрана, практически не меняя формы. Поэтому для исследования, изменения формы пакета, удобно брать энергию в пределах 10 ¸ 100 эВ.
|
|
|
Пространственные величины в этой работе измеряются в ангстремах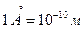 
. Начальную полуширину 
пакета будем менять в пределах 0.1 ¸ 10 Å. Необходимо поэкспериментировать с разными значениями . Если взять узкий пакет, то пакет очень быстро деформируется. Если же взять широкий пакет, проходит всю рабочую область экрана, практически не меняя формы.
Время будем измерять в фемтосекундах 
.
Задания.
Если электрон находится в состоянии с волновой функцией в виде волнового пакета (А.22), то это означает, что распределение плотности вероятности найти электрон в момент времени t в точке пространства с координатой x определяется следующей формулой (A.24).
(3)
Следующие 4 задания будут посвящены исследованию эволюции волнового пакета, заданного этой формулой.
Задание 1.
а) Запустить программу free_movement.m и получить картинку, показанную на Рис. 01. Подставить в программу free_movement.m данные своего варианта. Подбирая пространственные параметры xBegin, xEnd и временные параметры t 1, t 2, t 3, t 4 в этой программе, получить для своего варианта картину похожую на Рис.01.
Работу программы показать преподавателю. Подобранные параметры занести в конспект. Эти параметры нужно будет использовать в следующих заданиях.
Рис.01.
Положение пакета в разные моменты времени.
б) С помощью формул (1), (2) вычислить скорость электрона для своего варианта. Использовать единицы Å / фс (ангстремы на фемтосекунды), В приведенном примере энергия электрона равна 
, откуда получается следующая скорость.
Результат занести в конспект и показать преподавателю.
|
|
|
Задание 2.
а) Запустить программу Wave_Packet, файлы которой находятся в папке Wave_Packet. Запускать программу надо из файла main.m.
Рис.02.
Изменение амплитуды пакета со временем.
После запуска программы обнаружится, что полученная картина отличается от картины на Рис. 02. В верхней части окна отсутствует информация об изменении полуширины пакета от времени.
Поэтому вначале надо программу Wave_Packet изменить, добавив нужные строчки кода, что бы результат был таким же, как на Рис.02. Посмотрим, какие изменения надо произвести в функциях программы Wave_Packet.
Во-первых, рассмотрим функцию Work_Window. Эта функция создает рабочее окно и элементы управления (controls). В этой функции создаются 8 элементов управления, четыре типа ' pushbutton ' – управляющие кнопки, и четыре типа ' text ' – текстовые поля для вывода информации. Как оформляются элементы управления можно понять, если рассмотреть код функции Work_Window. Детали же можно посмотреть в справочной системе Help MATLAB.
У каждого элемента управления имеется свой дескриптор (handle), другими словами номер по которому система различает элементы управления. Дескрипторы можно обозначать любым набором символов без пробелов. В функции Work_Window дескрипторы обозначаются следующим образом: hBut1, hBut2, hBut3, hBut4, hTxtys1, hTxtys1T, hTxtys2, hTxtys2T. Для краткости будем элемент управления называть именем его дескриптора.
Рассмотрим следующие четыре элемента управления - hTxtys1, hTxtys1T, hTxtys2, hTxtys2T. Код этих элементов управления находится в конце функции Work_Window. Первый элемент управления hTxtys1T это текстовое поле, в котором находится надпись символа времени, и единица измерения времени ' t (fs) = '. Следующее текстовое поле hTxtys1 предназначено для показа текущего времени во время работы программы. Вначале в нем установлено значение ноль '0'. Следующие два элемента управления hTxtys2, hTxtys2T предназначены для вывода информации о величине амплитуды волнового пакет при движении пакета.
Для того чтобы передать дескрипторы элементов управления из функции Work_Window в другие функции программы, эти дескрипторы объявляются глобальными переменными. Для этого в начале функции Work_Window перед дескрипторами ставится служебное слово global.
|
|
|
Заметим, что элементы управления располагаются в рабочем окне программы, или можно сказать в графическом окне, в котором появляется вся графическая информация. Графическое окно создается функцией figure, и имеет дескриптор hFig1.
б) Задача студента добавить в конце функции Work_Window два элемента управления hTxtys3, hTxtys3T для вывода информации о полуширине пакета во время движения пакета. Не забыть в начале функции Work_Window описать дескрипторы как глобальные переменные.
Во-вторых, рассмотрим функцию Move_Packet. В начале функции Move_Packet с помощью функции set элементы управления делаются видимыми ' Visible on ', активными ' Enable on ' или не активными ' Enable off '.
в) Задача студента добавить две строчки кода, чтобы сделать видимыми два поля вывода hTxtys3, hTxtys3T.
Далее посмотрим на следующие строчки кода функции Move_Packet.
str = num2str(t);
set(hTxtys1,'String',str);
str = num2str(AFun(h,m,d0,t));
set(hTxtys2,'String',str);
Функция num2str переводит значение времени t в строчку str, которая затем появляется в поле вывода hTxtys1. Аналогично две следующие строчки кода переводят значение амплитуды пакета, которая вычисляется с помощью функции AFun(h,m,d0,t), в строчку str, и затем выводят результат в поле вывода hTxtys2.
г) Задача студента добавить в этом месте функции Move_Packet две строчки кода, чтобы вычислить значение полуширины пакета d (t) в момент t, перевести результат в строчку str и поместить в поле вывода hTxtys3.
д) Запустить измененную программу Wave_Packet и получить картинку, совпадающую с Рис. 02.
е) Подставить во вновь созданную программу Wave_Packet данные своего варианта и параметры из задания 1. Подбирая временной параметры dt – шаг по времени и время задержки изображения del в функции pause (del), получить для своего варианта картину плавного движения волнового пакета, со скорость не слишком маленькой и не слишком большой. В приведенном примере с энергией и полушириной пакета 
выбраны следующие временные параметры dt = 0.02, pause (0.02).
Работу программы показать преподавателю.
ж) Запустив программу Wave_Packet с помощью кнопки < Start > и останавливая движение волнового пакета с помощью кнопки < Stop > и затем, возобновляя движение с помощью кнопки < Move > заполнить следующую таблицу.
|
|
|
| |||||
| |||||
|
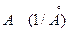
Для приведенного примера эта таблица может иметь следующий вид.
|
| 0.78 | 1.48 | 2.22 | 2.92 | 3.98 |
|
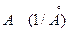
| 0.12293 | 0.96437 | 0.074723 | 0.060505 | 0.046406 |
|
| 4.5894 | 5.8503 | 7.5504 | 9.3246 | 12.1576 |
Таблицу занести в конспект и показать преподавателю.
Задание 3.
Запустить программу amplitude и получить картинку, показанную на Рис. 03. В этой программе строится зависимость амплитуды пакета от времени с помощью формулы (А.27). На полученную кривую нанесены значения амплитуды в 5 моментов времени, полученные в задании 2, и взятые из соответствующей таблицы. Для своего варианта подобрать нужные параметры, и получить картину похожую на Рис. 03.
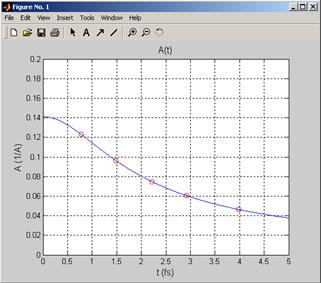
Рис.03.
Изменение амплитуды пакета со временем.
Работу программы показать преподавателю.
Задание 4.
Запустить программу half_width и получить картинку, показанную на Рис. 04. В этой программе строится зависимость полуширины пакета от времени с помощью формулы (А.26). На полученную кривую нанесены значения полуширины в 5 моментов времени, полученные в задании 2, и взятые из соответствующей таблицы. На картине показа также асимптотическая линия. Для своего варианта подобрать нужные параметры, и получить картину похожую на Рис. 04.
Рис.04.
Изменение полуширины пакета со временем.
Работу программы показать преподавателю.
Если электрон находится в состоянии с волновой функцией в виде волнового пакета (А.22), то это означает, что велика вероятность обнаружение электрона в данный момент времени t в области следующего размера.
.
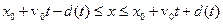В частности в начальный момент времени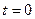 
этот интервал будет следующим.
.
Поэтому параметр 
определяет неопределенность координаты электрона. В квантовой механики неопределенность координаты 
принято определять, как среднеквадратичное отклонение 
. В приложении показывается, что среднеквадратичное отклонение координаты у волнового пакета (А.22) определяется формулой (B.55).
(4)
В квантовой механике показывается, что если имеется отличная от нуля неопределенность координаты электрона , то должна быть отличная от нуля неопределенность импульса электрона 
. Эти неопределенности связаны соотношением Гейзенберга. Соотношение неопределенности имеет следующий вид.
(5)
Так как существует разброс импульса электрона в некотором интервале, то можно говорить о вероятности электрону иметь то или иное значение импульса. В общем случае найти распределение плотности вероятности импульса электрона можно по формулам (B.42), (B.45), (B.46). Плотность вероятности импульса для волнового пакета (А.22) определяется формулой (B.49).
|
|
|
(6)
Рис.05.
Зависимость плотности вероятности импульса электрона от его импульса.
Оценим, какие значения импульса принимает электрон в данной работе. Возьмем, например, электрон с энергией 
. Тогда по формуле 
получим следующее значение импульса электрона 
. Получилась величина неудобная для использования в расчетах. Однако если расстояние измерять в ангстремах, а время в фемтосекундах, то получится приемлемый результат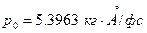 
. Поэтому дальше измерять импульс будем в единицах 
.
Распределение (6) показано на Рис. 05. Вертикальной зеленой линией отмечено положение среднего импульса электрона . Красными линиями отмечены значения импульсов 
и 
. Как показано в приложении неопределенность импульса 
для волнового пакета (А.22) определяется формулой (B.53).
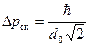(7)
Как видно из формул (4) и (7) соотношение неопределенность Гейзенберга (5) в этом случае принимает вид.
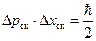(8)
Вероятность электрону иметь импульс в пределах 
определяется следующим интегралом.
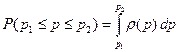(9)
В программе momentum_distribution строится распределение импульса Рис. 05 и вычисляется интеграл (9).
Задание 5.
а) Запустить программу momentum_distribution и получить картину, показанную на Рис. 05. Для своего варианта подобрать нужные параметры, и получить картину похожую на Рис. 05.
Работу программы показать преподавателю.
б) С помощью программы momentum_distribution найти средний импульс электрона , неопределенность импульса и вычислить интеграл (9). Кроме того, вычислить вероятности 
и 
. Заполнить следующую таблицу.
| 
|
| 
|
|
Для приведенного примера некоторые из этих величин соответственно равны.
|
|
|
|
|
|
| 17.0646 | 1.8562 | 0.6826 |
Таблицу занести в конспект и показать преподавателю.
Как показывает анализ, неопределенность импульса для волнового пакета (А.22) не изменяется со временем и определяется формулой (7). Неопределенность координаты 
напротив изменяется со временем. Как видно из рассмотренных выше заданий, ширина пакет растет со временем, а это означает, что растет со временем и неопределенность координаты. Анализ показывает, что для неопределенности координаты в любой момент времени справедлива формула.
(10)
В начальный момент времени неравенство Гейзенберга (5) для волнового пакета превращается в равенство (8). Затем при движении волнового пакета равенство превращается в неравенство, и по мере движения неравенство Гейзенберга усиливается.
в) Используя результаты задания 2, заполнить следующую таблицу.
|
| |||||
|
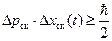
Для приведенного примера эта таблица может иметь следующий вид.
|
| 0.78 | 1.48 | 2.22 | 2.92 | 3.98 |
|
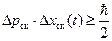
| 1.147 > 1 | 1.463 > 1 | 1.888 > 1 | 2.331 > 1 | 3.039 > 1 |
Таблицу занести в конспект и показать преподавателю.
Варианты к лабораторной работе.
| Номер варианта | , эВ
| , Å
|
| 1.25 | ||
| 1.25 | ||
| 1.25 | ||
| 1.25 | ||
| 1.25 | ||
| 1.25 | ||
| 1.5 | ||
| 1.5 | ||
| 1.5 | ||
| 1.5 | ||
| 1.5 | ||
| 1.5 | ||
| 1.75 | ||
| 1.75 | ||
| 1.75 | ||
| 1.75 | ||
| 1.75 | ||
| 1.75 | ||
Требования к отчету.
1. Лабораторная работа выполняется в тетради для лабораторных работ (отдельные листы не принимаются).
2. Графики выполняются в графических пакетах (за редким исключением на миллиметровки).
3. Предоставить отчеты по четырем заданиям, приведенным выше.
4. Выучить теоретический материал, данный в приложениях A и B.
5. Уметь выводить формулы из приложения A.
6. Уметь объяснять смысл формул приведенных в приложении B.
Приложение A.
Нахождение решения уравнения Шредингера для свободного электрона в виде волнового пакета.
Запишем уравнение Шредингера для свободного электрона
(A.1)
После преобразований уравнение Шредингера принимает вид
(A.2)
Это уравнение решаем с начальным условием
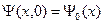(A.3)
Здесь 
- волновая функция электрона в начальный момент времени. Ищем решение уравнения (A.2) в виде интеграла Фурье
(A.4)
Подставляем (A.4) в (A.2) и получаем
(A.5)
Решение (A.4) можно теперь записать в следующем виде
(A.6)
Используем начальное условие (A.3), и из (A.6) получаем разложение начальной волновой функции электрона в интеграл Фурье.
(A.7)
К выражению (A.7) применяем обратное преобразование Фурье
(A.8)
Подведем итог проделанным преобразованиям. Итак, если известна волновая функция электрона 
в начальный момент времени, то после интегрирования (A.8) находим коэффициенты 
. Затем после подстановки этих коэффициентов в (A.6) и интегрировании, получаем волновую функцию электрона в произвольный момент времени в любой точке пространства.
Для некоторых распределений интегрирование можно провести в явном виде и получить аналитическое выражение для решения уравнения Шредингера. В качестве начальной волновой функции возьмем распределение Гаусса, модулированное плоской монохроматической волной.
(A.9)
Здесь - средний импульс электрона. Выбор начальной волновой функции в таком виде позволят получить решение уравнения Шредингера в виде волнового пакета.
Рассмотрим подробно свойства начальной волновой функции (A.9).
Во-первых, волновая функция нормирована на единицу.
(A.10)
Нормировка (A.10) легко доказывается, если использовать следующий табличный интеграл.
(A.11)
Во-вторых, если волновая функция нормирована на единицу, то квадрат модуля волновой функции является плотностью вероятности, нахождения электрона в данной точке пространства.
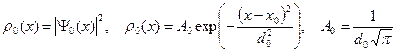(A.12)
Здесь величину 
будем называть амплитудой волнового пакета в начальный момент времени. Физический смысл амплитуды пакета – это максимальное значение распределения вероятности. На Рис.1 показан график распределения плотности вероятности.
Рис.1.
Распределение плотности вероятности в начальный момент времени.
Отметим некоторые особенности графика на Рис.1.
1. Координата 
– это точка на оси x, в которой распределение вероятности имеет максимальное значение. Поэтому можно сказать, что с наибольшей вероятностью можно обнаружить электрон вблизи точки .
2. Величина определят отклонение от точки 
, при котором величина распределения уменьшается в e раз по сравнению с максимальным значением.
(A.13)
В этом случае величину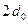 
называют шириной волнового пакета в начальный момент времени, а величину 
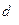– полушириной пакета.
3. Вычислим вероятность нахождения электрона в интервале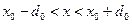 
.
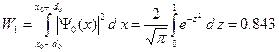(A.14)
Таким образом, вероятность обнаружить электрон в области с центром и полушириной равна 0.843. Эта вероятность близка к единице, поэтому обычно, об области с полушириной говорят, как об области, где находится электрон в начальный момент времени.
В-третьих, начальная волновая функция не является собственной функцией оператора импульса 
. Поэтому электрон в состоянии с волновой функцией не имеет определенного импульса, можно говорить только о среднем импульсе электрона. Вычислим средний импульс электрона.
(A.15)
Поэтому, величина в формуле (A.9) является средним значением импульса электрона. Формула (A.15) легко доказывается, если использовать табличный интеграл (A.11).
Таким образом, свойства начальной волновой функции разобраны. Теперь подставим функцию в интеграл Фурье (A.8) и найдем коэффициенты .
(A.16)
В интеграле (A.16) делаем следующую замену переменной интегрирования.
(A.17)
В результате интеграл (A.16) принимает следующий вид.
(A.18)
В результате получаем следующее выражение для коэффициентов .
(A.18)
Подставляем коэффициенты в формулу (A.6), получаем следующее интегральное выражение для волновой функции.
(A.19)
В интеграле (A.19) делаем следующую замену переменной интегрирования.
(A.20)
В результате интеграл (A.19) принимает следующий вид.
(A.21)
Окончательно получаем формулу для волнового пакета.
(A.22)
Легко видеть, что для начального момента времени 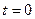формула (A.22) переходит в формулу (A.9) для начальной волновой функции. Найдем плотность вероятности для функции (A.22).
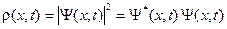(A.23)
Подставляем волновой пакет (A.22) в формулу (A.23), и в результате получаем следующее выражение.
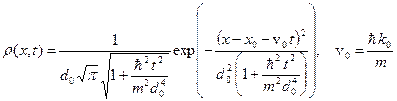(A.24)
Здесь центр волнового пакета, или максимум распределения плотности вероятности, движется со скоростью , равной следующей величине.
(A.25)
Полуширина волнового пакета увеличивается со временем, и определятся следующей формулой.
(A.26)
Амплитуда волнового пакета уменьшается со временем, и определятся следующей формулой.
(A.27)
Таким образом, распределение вероятности для волнового пакета можно записать в следующем виде.
(A.28)
На Рис.2. показано распределение вероятности в три последовательных момента времени.
Рис.2.
Распределение вероятности в три последовательных момента времени.
Приложение B.
Общие сведения о решении уравнения Шредингера.
Введение.
Движение квантовой частицы в общем случае описывается уравнением Шредингера:
. (B.1)
Здесь i – мнимая единица, h =1.0546´10-34 (Дж×с) - постоянная Планка. Оператор Ĥ называется оператором Гамильтона. Вид оператора Гамильтона зависит от типа взаимодействия электрона с внешними полями.
Если не учитывать спиновые свойства электрона, например, не рассматривать движение электрона в магнитном поле, то оператор Гамильтона можно представить в виде.
(B.2)
Здесь 
– оператор кинетической энергии:
, (B.3)
где m =9.1094´10-31 (кг) – масса электрона. Потенциальная энергия 
описывает взаимодействие электрона с внешним электрическим полем.
В данной лабораторной работе будет рассматриваться одномерное движение электрона вдоль оси x. Уравнение Шредингера в этом случае принимает следующий вид:
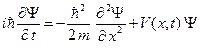. (B.4)
Уравнение (B.4) с математической точки зрения является дифференциальным уравнение в частных производных для неизвестной волновой функции Y = Y (x,t). Известно, что такое уравнение имеет определенное решение, если заданы соответствующие начальные и граничные условия. Начальные и граничные условия выбираются исходя из конкретной физической задачи.
Пусть, например, электрон движется слева направо с некоторым средним импульсом p0. Кроме того, в начальный момент времени t=0, электрон локализован в некоторой области пространства xm-d < x < xm+d. Здесь xm – центр области локализации электрона, а d – эффективная полуширина этой области.
В этом случае начальное условие будет выглядеть следующим образом:
. (B.5)
Здесь Y0(x) – волновая функция в начальный момент времени. Волновая функция это комплексная функция, поэтому графически удобно представлять не саму волновую функцию, а плотность вероятности.
Плотность вероятности, нахождения электрона в данном месте в данный момент времени выражается через волновую функцию следующим образом:
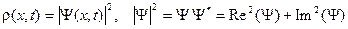. (B.6)
Заметим, что вероятности должна быть нормирована на единицу. Отсюда получаем условие нормировки волновой функции:
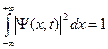. (B.7)
Распределение плотности вероятности в начальный момент времени
, (B.8)
можно изобразить графически. На Рис.3. показано возможное расположение электрона в начальный момент времени.
Рис.3.
Расположение электрона в момент t=0.
Из этого рисунка видно, что с наибольшей вероятностью электрон находится в точке xm. Буквой A будем обозначать амплитуду (максимальное значение) распределения вероятности. Из этого рисунка так же видно, как определяется ширина 2d или полуширина d распределения. Если распределение имеет экспоненциальный или гауссов характер, то ширину распределения определяют на уровне в e раз меньшем, чем максимальное значение.
На Рис.3. показан вектор среднего импульса электрона. Это означает, что электрон движется справа налево, и распределение вероятности так же будет перемещаться справа налево. На Рис.2. показано распределение вероятности в три последовательных момента времени. На Рис.2. видно, что максимум распределения xm(t) перемещается слева направо.
На Рис.2. можно заметить, что движение электрона справа налево сопровождается деформацией распределения плотности вероятности. Амплитуда A (t) уменьшается, а полуширина d(t) растет. Все указанные детали движения электрона можно получить, если решить уравнение Шредингера (B4) с начальным условием (B.5).
Резюме. В зависимости от постановки физической задачи может меняться вид уравнения Шредингера. При исследовании тех или иных физических явлений, описываемых уравнением Шредингера, выбираются нужные начальные и граничные условия для нахождения решения уравнения Шредингера.
Стационарные решения уравнения Шредингера.
Если электрон движется в постоянном по времени внешнем поле, то его потенциальная энергия не будет зависеть от времени. В этом случае одним из возможных решений уравнения Шредингера (B.4) является решение с разделяющимися переменными по времени t и по координате x.
Применяем известный в математике прием решения дифференциальных уравнений. Ищем решение уравнения (B.4) в виде:
. (B.9)
Подставляем (B.9) в уравнение (B.4) и получаем следующие соотношения:
. (B.10)
Здесь E – константа, которой в квантовой механике придается смысл полной энергии электрона. Соотношения (B.10) эквивалентны следующим двум дифференциальным уравнениям:
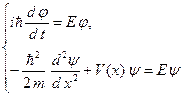. (B.11)
Первое уравнение в системе (B.11) имеет следующее общее решение:
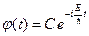. (B.12)
Здесь C – произвольная константа. Подставляем (B.12) в выражение (B.9) и получаем решение уравнения Шредингера (B.4) в виде:
, (B.13)
где функция y (x) удовлетворяет уравнению.
(B.14)
Константа C содержится в функции y (x).
Решение уравнения Шредингера (B.4) в виде выражения (B.13), называется стационарным решением уравнения Шредингера. Уравнение (B.14) называют стационарным уравнение Шредингера. Функцию y (x) называют волновой функцией, независящей от времени.
Состояние электрона, которое описывается волной функцией (B.13), называется стационарным состоянием. В квантовой механике утверждается, что в стационарном состоянии электрон обладает определенной энергией E.
Полученные результаты можно обобщить на уравнение Шредингера (B.1) для трехмерного движения электрона. Если оператор Гамильтона Ĥ не зависит явно от времени, то одним из возможных решений уравнения Шредингера (B.1) является стационарное решение следующего вида:
, (B.15)
где волновая функция 
удовлетворяет стационарному уравнению Шредингера.
(B.16)
Заметим, что уравнения (B.14) и (B.16) в квантовой механике имеют еще оно название. Эти уравнения являются уравнениями на собственные функции и собственные значения оператор
|
|
|
