 |
Туннелирование электрона через потенциальный барьер прямоугольной формы
|
|
|
|
Московский институт электронной техники
Кафедра КФН
Лабораторная работа 3
Туннелирование волнового пакета через прямоугольный барьер.
Общие указания.
1. В начале надо познакомиться с программой Square_ Barrier, которая моделирует туннелирование волнового пакета через прямоугольный барьер. Файлы программы находятся в папке Square_ Barrier. Программа запускается из файла main.m. Параметры задачи определяются в файле Data_Packet. В этом файле студент должен изменять параметры в соответствии с задачей своего варианта. Параметры, которые можно изменять в этом файле имеют следующий физический смысл.
1) 
- средняя энергия электрона (эВ).
2) 
- полуширина волнового пакета (Å).
3) 
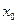- координата центра волнового пакета (Å).
4) 
- высота потенциального барьера (эВ).
5) 
- координаты, определяющие положение потенциального барьера (Å).
6) xBegin, xEnd – координаты, определяющие область пространства, в котором двигается волновой пакет.
7) dt – временной шаг.
2. Далее надо запустить программу Square_ Barrier из файла main.m и поэкспериментировать с управляющими элементами. Элементы управления имеют следующий смысл.
1) Start – запуск программы с начального положения.
2) Stop – остановка выполнения программы.
3) Move – возобновление работы программы с места остановки.
4) Close – грамотное завершение работы программы.
В верхней части графического окна программы выводятся изменяющиеся параметры программы, которые имеют следующий физический смысл.
1) t – текущее время, измеряется в фемтосекундах (фс).
2) 
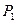- вероятность нахождения электрона перед барьером, которая вычисляется с помощью следующего интеграла.
. (1)
3) 
- вероятность нахождения электрона внутри барьера, которая вычисляется с помощью следующего интеграла.
|
|
|
. (2)
4) 
- вероятность нахождения электрона позади барьера, которая вычисляется с помощью следующего интеграла.
. (3)
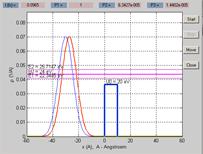
На Рис. 01 показана начальная стадия движения волнового пакета.
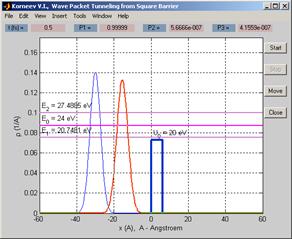
Рис.01.
Начальная стадия движения волнового пакета.
Программа Square_ Barrier моделирует движение электрона в состоянии с волновой функцией 
имеющей вид волнового пакета (смотри лабораторную работу 2, приложение А). Кривые на экране описывают распределение плотности вероятности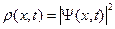 
в последовательные моменты времени. Для простоты будем называть волновым пакетом распределение плотности вероятности 
.
Синяя кривая на Рис. 01 показывает положение пакета в начальный момент времени. В качестве начального значения пакета берется гауссов волновой пакет (смотри лабораторную работу 2, приложение А, формула (А.9)). На Рис. 01 видно, что среднее положение пакета выбрано равным 
, а полуширина пакета равна 
.
Красная кривая показывает положение пакета в момент времени 
. В этот момент времени волновой пакет полностью находится слева от потенциального барьера. Поэтому вероятность найти электрон слева от потенциального барьера равна 
. Вероятность нахождения электрона внутри барьера и справа от барьера практически равна нулю.
На Рис. 01 прямоугольный потенциальный барьер изображен синими толстыми линиями. Показана также высота потенциального барьера в электрон-вольтах 
.
Светло-сиреневая линия показывает среднюю энергию электрона 
. Две темно-сиреневые линия показывают границы энергетического спектра волнового пакета. Соответствующие энергии 
определяются следующими формулами.
(4)
Здесь 
есть среднеквадратичное отклонение волнового числа от среднего значения 
, и определяется следующей формулой.
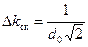(5)
Из формул (4), (5) видно, что чем меньше полуширина волнового пакета , тем больше ширина энергетического спектра 
у этого волнового пакета.
|
|
|
На Рис. 02 показан момент взаимодействия волнового пакета с потенциальным барьером.
Рис.02.
Момент взаимодействия пакета с потенциальным барьером.
Красная кривая показывает положение пакета в момент времени 
. На Рис. 02 показана часть пакета, которая отразилась от барьера, и двигается налево, удаляясь от барьера. Величина этой части пакета определяет вероятность электрону быть отраженным от барьера. В данном примере эта вероятность равна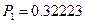 
.
На Рис. 02 показана также часть пакета, которая прошла через барьер, туннелировала через барьер, и двигается направо, удаляясь от барьера. Величина этой части пакета определяет вероятность туннелирования электрона через барьер. В данном примере эта вероятность равна 
.
Наконец Рис. 02 показана часть пакета, которая локализована внутри барьера. Величина этой части пакета определяет вероятность нахождения электрона внутри барьера. В данном примере эта вероятность равна 
.
3. Коэффициент отражения от барьера R (Reflectivity), и коэффициент пропускания через барьер T (Transmissivity), в задаче о туннелировании волнового пакета, определяются следующими формулами.
(6)
Заметим, что формулы (6) применяются для достаточно больших моментов времени. Нужно чтобы произошло взаимодействие волнового пакета с потенциальным барьером. Части волнового пакета разбежались от барьера, а вероятность нахождения электрона внутри барьера стала равной нулю 
. Строго это выполняется в пределе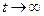 
.
Реально будем выбирать такие времена, когда вероятность будет близка к нулю, например 
.
На Рис. 03 показан момент, при котором можно определить коэффициенты 
.
Рис. 03.
Момент для определения коэффициентов .
Отметим, что на Рис. 03 увеличены размеры пространства, в котором движется пакет по сравнению с Рис. 02. Это сделано, для того чтобы в рабочем пространстве уместились отраженная и прошедшая части волнового пакета. В этом случае можно считать, что волновой пакет равен нулю за пределами рабочего пространства. Тогда вероятности 
будут совпадать с коэффициентами отражения и пропускания.
(7)
В данном примере получаем следующие коэффициенты отражения и пропускания.
|
|
|
Сумма этих коэффициентов отличается от единицы 
. Это связано с тем, что вероятность нахождения электрона в барьере равна примерно 
.
На следующем Рис. 04 выбрано еще большее время движения пакета и большее рабочее пространство.
Рис. 04.
Момент для определения коэффициентов .
В данном примере получаем следующие коэффициенты отражения и пропускания.
Сумма этих коэффициентов отличается от единицы 
на одну сотую. Таким образом, для вычисления коэффициентов отражения и пропускания с заданной точностью нужно подобрать достаточно большое рабочее пространство. С другой стороны, слишком большие пространственные размеры замедляют работу программы, и потребуется много времени для выполнения заданий лабораторной работы.
4. Заметим, что можно ускорить движение пакета, увеличивая временной шаг dt. Однако слишком большой шаг делает движение пакета не плавным, а рывками.
В программе Square_ Barrier предусмотрен флаг flagStop, который позволяет менять режим работы программы. Если флаг равен нулю flagStop = 0, то программа может работать в течение любого времени и части волнового пакета могут уйти за пределы рабочего пространства. Если же флаг равен единице flagStop = 1, то прекращается движение пакета в тот момент, когда части волнового пакета, достигают границ рабочего пространства.
Рекомендуется выбрать значение флага flagStop = 1.
Правила работы с программой Square_ Barrier.
Программа Square_ Barrier используется, в данной лабораторной работе, для нахождения коэффициента пропускания T, при заданных параметрах задачи  .
Чтобы получить коэффициент T с заданной точность, нужно правильно настроить работу программы.
1. Если вероятность  , то коэффициент пропускания будет равен  с точностью 0.01. Если это условие не выполняется нужно изменить пространственные размеры задачи.
2. Центр волнового пакета 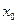нужно выбрать так, чтобы волновой пакет в начальный момент времени располагался посередине между левой границей и барьером. Причем пакет не должен налезать на барьер и на границу. На Рис. 05 (a, b) показано неправильное начальное расположение волнового пакета. На Рис. 05 (c) показано правильное расположение пакета относительно потенциального барьера и границ рабочего пространства.
3. Чтобы программа вычислила коэффициент прохождения T с указанной точностью, размеры рабочего пространства  должны быть достаточно большими. В рабочем пространстве должны располагаться отраженная от барьера и прошедшая через барьер части волнового пакета. Причем вероятность нахождения электрона в области барьера при этом должна быть мала . На Рис. 06 (a) показан неправильный выбор размеров рабочего пространства для вычисления коэффициента отражения с заданной точностью. На Рис. 06 (b) показан правильный выбор размеров рабочего пространства для вычисления коэффициента отражения с заданной точностью.
4. Чтобы ускорить работу программы можно увеличить временной шаг dt.
|
|
|
|
a b c
Рис. 05.
Расположение пакета в начальный момент времени, a, b – неправильное, c – правильное.
a b
Рис. 06.
Выбор пространственных параметров для вычисления коэффициента прохождения с заданной точностью, a – неправильный выбор, b – правильный выбор.
Задание 1.
Нахождение зависимости коэффициента пропускания T волнового пакета от средней энергии электрона E 0.
Для своего варианта с помощью программы Square_ Barrier заполнить таблицу для нахождения зависимости 
. Высоту потенциального барьера положить равной 
. Ширину барьера a и полуширину волнового пакета d 0 взять в задании для своего варианта.
| E 0 эВ | 15.0 | 17.5 | 20.0 | 22.5 | 25.0 | 27.5 | 30.0 | 32.5 | 35.0 | 37.5 |
| T |
| E 0 эВ | 40.0 | 42.5 | 45.0 | 47.5 | 50.0 | 52.5 | 55.0 | 57.5 | 60.0 |
| T |
Для примера с параметрами 
эта таблица имеет вид.
| E 0 эВ | 15.0 | 17.5 | 20.0 | 22.5 | 25.0 | 27.5 | 30.0 | 32.5 | 35.0 | 37.5 |
| T | 0.012 | 0.041 | 0.152 | 0.463 | 0.825 | 0.911 | 0.848 | 0.825 | 0.857 | 0.910 |
| E 0 эВ | 40.0 | 42.5 | 45.0 | 47.5 | 50.0 | 52.5 | 55.0 | 57.5 | 60.0 |
| T | 0.959 | 0.986 | 0.992 | 0.984 | 0.971 | 0.961 | 0.957 | 0.958 | 0.964 |
График зависимости строится в программе Task01.m. В этой же программе строится зависимость 
для монохроматического электрона по формулам (А.8), (А.9). Для приведенного примера результат показан на Рис. 07.
Рис. 07.
Зависимость коэффициента пропускания от энергии электрона. Синяя линия – монохроматический электрон. Зеленая линия – волновой пакет.
После заполнения таблицы с помощью программы Square_ Barrier, эти результаты использовать в программе Task01 для построения графика зависимости .
Напомним, что в программе Square_ Barrier и программе Task01 нужно подставить параметры своего варианта.
Задание 2.
Нахождение зависимости коэффициента пропускания T волнового пакета от полуширины пакета d 0.
|
|
|
Для своего варианта с помощью программы Square_ Barrier заполнить таблицу для нахождения зависимости 
. Ширину потенциального барьера положить равной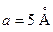 
. Высоту барьера U 0 и среднюю энергию волнового пакета E 0 взять в задании для своего варианта.
| |||||||||
| T |
Для примера с параметрами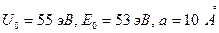 
эта таблица имеет вид.
|
| |||||||||
| T | 0.224 | 0.168 | 0.132 | 0.103 | 0.080 | 0.062 | 0.048 | 0.037 | 0.028 |
График зависимости строится в программе Task01.m. Для приведенного примера результат показан на Рис. 08.
Рис. 08.
Зависимость коэффициента пропускания от полуширины волнового пакета.
Варианты к заданию 1.
| Номер варианта | 
| 
|
| 2.0 | 5.0 | |
| 2.1 | 5.0 | |
| 2.2 | 5.0 | |
| 2.3 | 5.0 | |
| 2.4 | 5.0 | |
| 2.5 | 5.0 | |
| 2.0 | 5.5 | |
| 2.1 | 5.5 | |
| 2.2 | 5.5 | |
| 2.3 | 5.5 | |
| 2.4 | 5.5 | |
| 2.5 | 5.5 | |
| 2.0 | 6.0 | |
| 2.1 | 6.0 | |
| 2.2 | 6.0 | |
| 2.3 | 6.0 | |
| 2.4 | 6.0 | |
| 2.5 | 6.0 | |
| 2.0 | 6.5 | |
| 2.1 | 6.5 | |
| 2.2 | 6.5 | |
| 2.3 | 6.5 | |
| 2.4 | 6.5 | |
| 2.5 | 6.5 | |
| 2.0 | 7.0 | |
| 2.1 | 7.0 |
Варианты к заданию 2.
a =5 
| Номер варианта | E 0, эВ |  , эВ
|
| 19.9 | ||
| 19.8 | ||
| 19.7 | ||
| 19.6 | ||
| 29.9 | ||
| 29.8 | ||
| 29.7 | ||
| 29.6 | ||
| 39.9 | ||
| 39.8 | ||
| 39.7 | ||
| 39.6 | ||
| 49.9 | ||
| 49.8 | ||
| 49.7 | ||
| 49.6 | ||
| 59.9 | ||
| 59.8 | ||
| 59.7 | ||
| 59.6 | ||
| 59.5 |
Приложение A.
Туннелирование электрона через потенциальный барьер прямоугольной формы
Решаем уравнение Шредингера
(А.1)
с потенциальной энергией в виде прямоугольного барьера
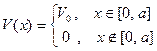
Здесь 
- высота барьера, 
- ширина барьера. Уравнение (А.1) решаем с начальным условием 
, где волновая функция начального состояния электрона имеет вид.
(А.2)
Здесь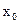 
- координата центра пакета, d 0 - ширина пакета, 
- волновое число электрона, которое связано со средним импульсом 
электрона, и со средней кинетической энергией 
электрона.
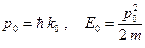
Плотность вероятности начального распределения дается формулой
На рисунке показано взаимное расположение потенциального барьера и волнового пакета электрона в начальный момент времени. Толстой линией показана средняя кинетическая энергия электрона
V (x)
k 0 V 0
E 0
x 0 0 a x
После взаимодействия с барьером пакет 
разделяется на части. Одна часть отражается и уходит налево, и позволяется найти коэффициент отражения по формуле
(А.3)
Другая часть проходит через барьер и уходит направо, и позволяется найти коэффициент пропускания по формуле
(А.4)
Еще она часть находится в области барьера
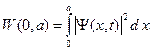(А.5)
Так как волновая функция нормирована на единицу
то коэффициенты R, T, W связаны соотношением
(А.6)
Во время работы пакета nsse в каждый момент времени вычисляются значения коэффициентов отражения R и пропускания T. Чтобы вывести их на экран, надо нажать клавишу F1. Можно убедиться, что вычисленные программой значения R, T удовлетворяют неравенству
Это находится в соответствие с формулами (А.3) – (А.6)
Если рассматривать туннелирование монохроматических электронов, то для коэффициентов отражения и пропускания существуют простые аналитические формулы. Монохроматический электрон, это электрон у которого энергия, импульс и волновое число имеют определенные значения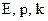 
. Связь между этими величинами такая же, как и для средних величин 
свободного электрона, движение которого описывается волновым пакетом (А.2)
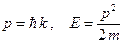
Волновая функция монохроматического электрона имеет вид
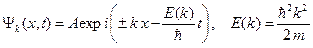(А.7)
Плюс и минус перед k означает, что электрон движется направо или налево. Для электрона с заданной энергией E коэффициент пропускания T задается следующими формулами.
Если 
, то для T справедлива формула
(А.8)
Если 
, то T вычисляется по другой формуле
(А.9)
Если ширину барьера a измерять в Å (ангстремах), энергии E, V0 в eV (электрон-вольтах), то вычисления в формулах (А.8), (А.9) надо выполнять по формулам
(А.10)
Электрон, движение которого описывается волновым пакетом, не имеет определенной энергии E. Это связано с тем, что начальный волновой пакет 
является суперпозицией волновых функций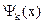 
(А.11)
с разными волновыми числами k и, соответственно, разными энергиями E = E(k) (А.7).
Это можно увидеть, разложив в интеграл Фурье.
(А.12)
Здесь коэффициенты C(k) имеют физический смысл. Так |C(k)|2 – плотность вероятности того, что электрон в состоянии имеет волновой число k и энергию E(k)
(А.13)
Коэффициенты C(k) можно найти, выполнив обратное преобразование Фурье
Тогда плотность вероятности для волнового числа будет определяться формулой
(А.14)
На рисунке приведены распределения |F0(x)|2 и |C(k)|2
|F0(x)|2 |C(k)|2
|F0(x0)|2 /e |C(k0)|2 /e
x0–ap x0 x0+ap x k0–1/ap k0 k0+1/ap k
Из этих рисунков видно, что электрон в момент времени t = 0 локализован в интервале x0–ap < x < x0+ap, где ap - полуширина пакета. Тогда величину Dx = 2ap можно назвать неопределенность координаты электрона. Аналогично волновые числа электрона лежат в интервале k0–1/ap < k < k0+1/ap и величину Dk = 2/ap можно назвать неопределенность волнового числа электрона.
Если вспомнить, что импульс электрона p и волновое число k связаны соотношением
то неопределенность электрона можно найти по формуле
Отсюда получаем соотношение неопределенности Гейзенберга
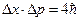
Кроме того, благодаря связи (А.13) энергия электрона E также имеет разброс DE вокруг среднего значения E0
(А.15)
Если ширину пакета ap измерять в Å, энергию E в eV, то имеем вычислительную формулу
Таким образом, локализованный электрон, волновая функция которого имеет вид волнового пакета, не имеет определенной энергии. Можно только говорить о средней энергии E0, и интервале DE, в котором лежит энергия электрона. Поэтому туннелирование такого электрона через потенциальный барьер, будет отличаться от результатов, поученным по формулам (А.8), (А.9) для монохроматического электрона. Результат будет зависеть от того, какие энергии принимают участие в формировании волнового пакета (А.12)
Из формулы (А.15) видно, что чем шире волновой пакет, тем меньше разброс в энергиях, и тем ближе рассматриваемый электрон к монохроматическому электрону
|
|
|
