 |
Метод элементарных преобразований
|
|
|
|
ПП 2. ОПРЕДЕЛИТЕЛИ И Матрицы
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
1. Виды матриц
Матрицей размерности  называется прямоугольная таблица чисел
называется прямоугольная таблица чисел  :
:
 ,
,
Частные виды матриц
 - квадратная нулевая,
- квадратная нулевая,  - матрица-строка,
- матрица-строка,
 - матрица-столбец,
- матрица-столбец, 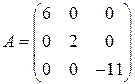 - квадратная диагональная,
- квадратная диагональная,
 - верхняя треугольная,
- верхняя треугольная,  - единичная.
- единичная.

 -т ранспонированная,
-т ранспонированная,
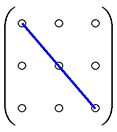 ,
,  - главная и побочная диагонали.
- главная и побочная диагонали.
2. Операции над матрицами
Равенство 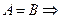
 .
.
Сумма 
 ;
;  .
.
Умножение на число 
 ;
;
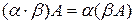 ,
, 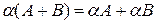 ,
,  .
.
Произведением матрицы  размерности
размерности  на матрицу
на матрицу  размерности
размерности  называется матрица
называется матрица  размерности
размерности  , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:

 ,
,  .
.

Иначе: элемент, стоящий на пересечении i- й строки и j- го столбца матрицы произведения  , равен сумме произведений элементов i- й строки матрицы А на соответствующие элементы j- го столбца матрицы В.
, равен сумме произведений элементов i- й строки матрицы А на соответствующие элементы j- го столбца матрицы В.

Число столбцов первой матрицы равно числу строк второй матрицы.
В общем случае A´B¹B´A, если A´B=B´A, то матрицы перестановочные (коммутирующие).
Свойства:
(A ´ B) ´ C = A ´ (B ´ C) (A ´ B) ´ C = A ´ (B ´ C).
(A + B) ´ C = A ´ C + B ´ C.
A ´ (B + C) = A ´ B + A ´ C.
A ´ E = E ´ A = A.
A ´ Æ = Æ ´ A = Æ.
(A ´ B)PT P= B P T P´ A PTP.
 .
.
Элементарные преобразования матриц:
§ транспонирование;
§ перестановка строк (столбцов);
§ умножение строки (столбца) на число  ;
;
§ прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число;
§ отбрасывание нулевой строки (столбца) матрицы.
3. Обратная матрица.
Квадратная матрица  n –го порядка называется вырожденной, если определитель этой матрицы равен нулю,
n –го порядка называется вырожденной, если определитель этой матрицы равен нулю,  , и невырожденной, если
, и невырожденной, если  .
.
Матрица А P-1P называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:  .
.
|
|
|
Основные методы вычисления обратной матрицы
Метод присоединенной матрицы
Теорема о существовании и единственности обратной матрицы.
Если матрица  не вырождена, то существует, и притом единственная, обратная матрица
не вырождена, то существует, и притом единственная, обратная матрица  , равная
, равная  , где
, где  - присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы).
- присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы).
1˚.  .
.
2˚.  .
.
3˚.  .
.
4˚.  .
.
Алгоритм нахождения обратной матрицы с помощью присоединенной матрицы:
1. Находим  , проверяем
, проверяем 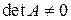 .
.
2. Находим  - все миноры матрицы
- все миноры матрицы  .
.
3. Определяем  .
.
4. Строим матрицу алгебраических дополнений  и транспонируем:
и транспонируем:  .
.
5. Делим каждый элемент матрицы на  :
:  .
.
Метод элементарных преобразований
Для невырожденной матрицы А n -го порядка построим прямоугольную матрицу  размера
размера 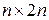 , приписывая к А справа единичную матрицу. Используя элементарные преобразования над строками, приводим эту матрицу к виду
, приписывая к А справа единичную матрицу. Используя элементарные преобразования над строками, приводим эту матрицу к виду  .
.
4. Решение матричных уравнений

Если  ,
,  - известные матрицы, а
- известные матрицы, а  – неизвестная, то равенство вида
– неизвестная, то равенство вида 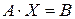 называется матричным уравнением.
называется матричным уравнением.
Основные типы матричных уравнений:
1.  . Матрица
. Матрица  должна быть квадратной,
должна быть квадратной,  . Умножим уравнение на
. Умножим уравнение на  слева:
слева:  ,
, 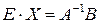 ,
, 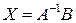 .
.
2.  . Матрица
. Матрица  должна быть квадратной,
должна быть квадратной,  . Умножим уравнение на
. Умножим уравнение на  справа:
справа:  .
.
3.  . Матрицы
. Матрицы  и
и  должны быть квадратными,
должны быть квадратными,  ,
,  . Умножим на
. Умножим на  слева:
слева:  . Умножим на
. Умножим на  справа:
справа:  .
.
5. Ранг матрицы.
Пусть в матрице  размерности
размерности  выбраны
выбраны  строк и
строк и  столбцов, причем
столбцов, причем  . Тогда элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу
. Тогда элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу  -го порядка. Определитель
-го порядка. Определитель  этой матрицы называется минором
этой матрицы называется минором  -го порядка матрицы
-го порядка матрицы  .
.
Рангом матрицы  называется число, равное максимальному по рядку
называется число, равное максимальному по рядку  отличных от нуля миноров
отличных от нуля миноров  этой матрицы:
этой матрицы:
 .
.
Матрицы называются эквивалентными, что обозначается  , если
, если 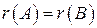 .
.
Ранг матрицы  вычисляется методом окаймляющих миноров или методом элементарных преобразований.
вычисляется методом окаймляющих миноров или методом элементарных преобразований.
|
|
|
Метод окаймляющих миноров
Пусть в матрице  элемент
элемент  , тогда
, тогда 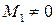 и
и  . Окаймляем этот элемент элементами
. Окаймляем этот элемент элементами  -го столбца и
-го столбца и 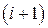 - й строки, получаем минор 2-го порядка:
- й строки, получаем минор 2-го порядка:

Если  , то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка. Если все миноры второго порядка равны нулю, то
, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка. Если все миноры второго порядка равны нулю, то  ; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то
; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то  .
.
Выбираем отличный от нуля минор 2-го порядка  и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие:
и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие:  , но все
, но все  .
.
Метод элементарных преобразований
Элементарные преобразования матрицы не меняют ее ранга.
Для определения ранга матрицы  методом элементарных преобразований следует:
методом элементарных преобразований следует:
1. Переставить строки так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2. Все элементы первого столбца, кроме  , обратить в ноль:
, обратить в ноль:
 .
.
3. Повторить операцию со второй строкой: во втором столбце должен быть ненулевой элемент, после чего все элементы второго столбца, кроме  и
и  , обратить в ноль.
, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
 .
.
Тогда ранг матрицы  =
= 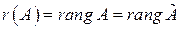 .
.
| ПП 2. ОПРЕДЕЛИТЕЛИ И Матрицы | ||
| № п/п | Задание | Ответ |
| TUПП 2.№1.UT | Найдите  .
Решение: .
Решение:  . .
| 
|
| TUПП 2.№2. | Найдите  .
Решение: .
Решение:  . .
| 
|
| ПП 2. № 3. | Найдите 3 А +2 В, если  Решение:
Решение:  . .
| 
|
| ПП 2. № 4. | Найдите С = А ´ В, если  Решение: Размерность матрицы А (2´3), размерность матрицы В (3´2), число столбцов матрицы А совпадает с числом строк матрицы В, в результате получится матрица С, размерность которой (2 ´ 3).
Решение: Размерность матрицы А (2´3), размерность матрицы В (3´2), число столбцов матрицы А совпадает с числом строк матрицы В, в результате получится матрица С, размерность которой (2 ´ 3).
 , ,  , ,  , ,  . .
 . .
| 
|
| ПП 2. № 5. | Найдите С = А´ В,
если  , ,  .
Решение: .
Решение:  , ,  , ,  , ,  , ,  , ,  . .  
| 
|
| ПП 2. № 6. | Найдите А´ В,
если  , ,  .
Решение: .
Решение:
 .
(размерность матрицы C .
(размерность матрицы C  ). ).
| 
|
| ПП 2. № 7. | Найдите А´В и В´А,
если  Решение:
Решение:  , ,
 . .
|  , ,
 . .
|
| ПП 2. № 8. | Найдите все матрицы, перестановочные с данной  .
Решение: Запишем вторую матрицу в виде .
Решение: Запишем вторую матрицу в виде  и найдем произведения и найдем произведения  и и  : :  , ,  . .  где
где  и и  – произвольные числа. – произвольные числа.
| 
|
| ПП 2. № 9. | Найдите матрицу, обратную для матрицы  .
Решение:
1) .
Решение:
1)  .
2) .
2)  .
3) .
3)  .
4) .
4) 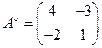 , ,  .
5) .
5)  .
Проверка: .
Проверка:

| 
|
| ПП 2.№10. | Методом присоединенной матрицы найдите матрицу, обратную к матрице
 .
Решение:
1) Находим .
Решение:
1) Находим  , проверяем , проверяем  : : 
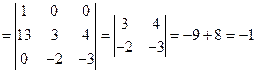 .
2) Находим .
2) Находим  - все миноры матрицы - все миноры матрицы  : :  
   
 
 3) Определяем
3) Определяем  : :  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  .
4) Строим матрицу алгебраических дополнений .
4) Строим матрицу алгебраических дополнений  и транспонируем ее: и транспонируем ее:

 , ,
 .
5) Делим каждый элемент матрицы на .
5) Делим каждый элемент матрицы на  : :  : :  . .
| 
|
| ПП 2.№11. | Методом элементарных преобразований строк найдите матрицу, обратную к матрице 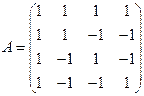 .
Решение: Составляем и преобразуем вспомогательную матрицу .
Решение: Составляем и преобразуем вспомогательную матрицу  : :    . .
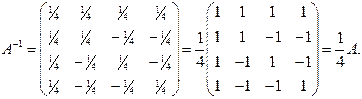
| 
|
| ПП 2.№12. | Решите матричное уравнение  , где , где  .
Решение: Вычислим .
Решение: Вычислим 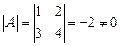 , значит, матрица A – невырожденная. Построим матрицу A P–1 P, обратную матрице A, двумя способами. 1) Метод присоединенной матрицы: , значит, матрица A – невырожденная. Построим матрицу A P–1 P, обратную матрице A, двумя способами. 1) Метод присоединенной матрицы:
 . 2) Метод элементарных преобразований строк: . 2) Метод элементарных преобразований строк:  . Записываем решение матричного уравнения: . Записываем решение матричного уравнения:  =
=  . .
| 
|
| ПП 2.№13. | Решите матричное уравнение  , где , где 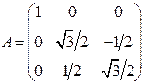 , ,  , ,  , ,  .
Решение:
Запишем уравнение в виде .
Решение:
Запишем уравнение в виде  .
Умножим уравнение .
Умножим уравнение  слева на слева на  и справа на и справа на  : :  , ,  , тогда , тогда  .
Найдем .
Найдем 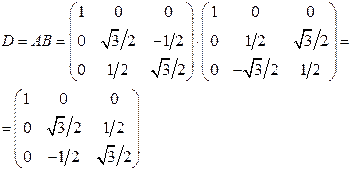 ; Вычислим ; Вычислим  и и  . .    , , 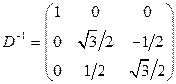 . .  , ,
 .
Тогда .
Тогда  . .
| 
|
| ПП 2.№14. | Найдите ранг матрицы  .
Решение: .
Решение:  ; ;  , ,  , ,  ; ;  . .
| |
| ПП 2.№15. | Вычислите ранг матрицы  методом элементарных преобразований.
Решение: методом элементарных преобразований.
Решение:        , rang A = 2. , rang A = 2.
| |
| ПП 2.№16. | Вычислите ранг матрицы  .
Решение: .
Решение:               
           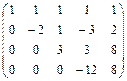 . В левом верхнем углу матрицы стоит определитель треугольного вида, который равен произведению элементов, стоящих на его главной диагонали . В левом верхнем углу матрицы стоит определитель треугольного вида, который равен произведению элементов, стоящих на его главной диагонали  , значит ранг матрицы равен четырем. , значит ранг матрицы равен четырем.
|
|
|
|
|
|
|


