Пpедусмотpеть pазpешение аваpийных ситуаций.

Вариант 1

1. Составить алгоритм для вычисления функции:
   
2. Даны уравнения прямых а₁х+b₁y=c₁, a₂x+b₂y=c₂, a₃x+b₃y=c₃. Выяснить, какие из этих прямых параллельны и указать, если таковых не имеется.
3. Даны две окружности заданные уравнениями (х-а₁)²+(у-b₁)²=r₁² и (х-а₂)²+(у-b₂)²=r₂². Определить количество точек пересечения и найти их координаты.
4. Составить алгоритм вычисления площадей различных геометрических фигур

 

Вариант 2

1. Найти max (a, b).

2. В какой четверти координатной плоскости находится точка с координатами x, y (xy<>0).

3. Даны два действительных числа а и b. Сравнить их целые части, и если они равны, то поменять местами их дробные части, в противном случае округлить эти числа.

4. Составить алгоритм вычисления площадей различных геометрических фигур

Вариант 3

1. Дана точка М(x, y). Присвоить z = 1, если точка внутри эллипса 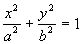и z = 0, если точка вне эллипса.

2. Если сумма двух различных чисел меньше единицы, то наименьшее заменить полусуммой, в противном случае меньшее заменить суммой.

3. Даны прямая и окружность, заданные уравнениями у=кх+b и (х-а)²+(у-b)²=r². Определить, сколько точек пересечения имеют прямая и окружность и найти координаты этих точек.

4. Составить алгоритм вычисления значения функции

 

Вариант 4

1. Вычислить y(x), если y = x² при x > 1 и y = x при x <= 1.

2. Даны различные действительные числа x, y, z, d. Найти max(max(x, y), max(x, z), max(z, d)).

3. Даны две прямые, заданные уравнениями у=к₁x+b₁ и y=k₂x+b₂. Если эти прямые параллельны, то определить расстояние между ними.

4. Составить алгоритм вычисления значения функции

Вариант 5

1. Вычислить:

2. Даны три действительных числа. Определить, что больше, сумма или произведение этих чисел. Если сумма больше произведения на число меньшее единицы, то вывести 0, и противном случае вывести 1.

3. Дана точка М(х, у). Проверить, принадлежит ли точка окружности единичного радиуса. Если принадлежит, то уменьшить координату х на единицу, а у увеличить на значение х.

4. Найти остаток от деления целой части значения функции z = ln(x²+ab) на 7 и, в зависимости от его величины, напечатать сообщение об одном из дней недели, пронумеровав их от 0 до 6.

Вариант 6

1. Даны два отрезка [a, b], [c, d] на прямой. Установить, имеют ли они общие точки или нет.

2. Найти значение z, если

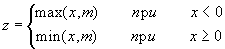
3. Определить параллельны ли прямые, заданные уравнениями у=к₁x+b₁ и y=k₂x+b₂. Если они параллельны, то найти координаты точек пересечения с осью ОХ (к₁, к₂ <> 0).

4. Даны три числа а, b, с, удовлетворяющие аксиоме треугольника и число р. Выполнить следующие действия: если р=1 - найти периметр треугольника; если р=2 - найти площадь треугольника; если р=3 - найти угол а. Иначе напечатать слово "треугольник".

 

Вариант 7

1. Дана точка М(x, y). Присвоить z = 1, если точка принадлежит окружности с радиусом R и центром в точке (a, b) и z = 0 в противном случае.

2. Даны отрезки [a, b] и [c, d] и точка A с координатой х. Определить, принадлежит ли данная точка одному из этих отрезков, обоим или лежит вне их.

3. Найти значение х и у при заданных значениях a и b:
,

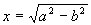4. Найти остаток от деления целого выражения а=(с+d)(2k-m) на 5 и вывести сообщение о величине остатка. Если остаток равен 0, присвоить а значение целой части выражения. При нечетном остатке напечатать "нечетное число", при четном - "четное число"

Вариант 8

1. Вычислить функцию f(x), если f(x) = e^-x при х >= 0 и f(x) = cos x при х < 0.

2. Даны два действительных числа x и y. Если наименьшее из них отрицательно, то заменить его нулем, в противном случае единицей.

3. Если w <> 0 и, при этом, w < 0.5, то поменять знак w, а если w = 0, присвоить w единицу.

4. Написать программу, которая по номеру машины выводит фамилию студента, сидящего за ней.

Вариант 9

1. Составить алгоритм для вычисления y = t² - t -1, где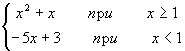

2. Определить, существует ли треугольник со сторонами a, b, c, и если существует, то является ли он равносторонним, равнобедренным или разносторонним.

3. Вывести сообщение о количестве корней квадратного уравнения и найти эти корни.

4. Найти остаток от деления целой части выражения z = cos(x²+1) на 4 и, и зависимости от его величины, напечатать сообщение об одном из времен года, пронумеровав их от 0 до 3.

Вариант 10

1. Составить алгоритм решения уравнения .

2. Даны действительные числа х1, х2, х3, y1, y2, y3. Принадлежит ли начало координат треугольнику с вершинами (x1, y1), (x2, y2), (x3, y3)?

3. Даны три числа. Определить, существует ли треугольник со сторонами длиной a, b, c и, если существует, то найти его параметр и площадь.

4. Найти остаток от деления целого выражения c = k(a+b) на 4 и вывести сообщение о величине остатка. Если остаток равен 0, то значение переменной оставить без изменения, если 1 или 3 - уменьшить на величину остатка, если 2 - увеличить на величину остатка.

Вариант 11

1. Составить алгоритм вычисления модуля |5x - 4|.

2. Даны действительные числа x, y. Если x и y отрицательные, то х присвоить модуль х. Если отрицательное одно из них, то увеличить у на 0.5. Если оба числа отрицательные, то увеличить х в 10 раз.

3. Определить направление ветвей параболы y=ax²+by²+c. Найти точки пересечения параболы с осью OX.

4. По номеру дня недели (1,2,3,4,5,6,7) указать название этого дня. Указать рабочие и выходные дни.

Вариант 12

1. Составить алгоритм вычисления функции:

2. Даны три действительных числа х, у, z и отрезок [a, b]. Заменить на нули те из них, которые принадлежат отрезку и на единицы - остальные.

3. Даны два числа. Если они не равны, то найти их сумму и произведение. Если произведение больше суммы, то определить на сколько.

4. Найти остаток от деления целой части выражения sin(a+b)0.5c на 4 и вывести на экран сообщение о величине остатка. Если остаток равен 0, то значение выражения заменить на его целую часть. Если остаток равен 1, значение выражения заменить на его дробную часть. В остальных случаях оставить без изменения.

Вариант 13

1. Составить алгоритм вычисления корня .

2. Даны различные действительные числа a, b, c, d. Найти max (max(a, b), max(a, c), max(a, d)).

3. Даны три числа a, b, c, удовлетворяющие аксиомам треугольника. Если треугольник равносторонний, то найти его площадь. Если треугольник равнобедренный, то найти периметр и угол между равными сторонами.

4. В зависимости от времени года "весна", "лето", "осень", "зима" определить погоду "тепло", "жарко", "холодно", "очень холодно".

 

Вариант 14

1. Составить алгоритм вычисления функции y=lg(3x-6).

2. Известно, что из четырех чисел a1, a2, a3, a4 одно отлично от трех других, равных между собой. Присвоить номер этого числа переменной n.

3. Решить биквадратное уравнение.

4. Составить программу вычисления значения функции

Вариант 15

1. Напечатать координаты той из точек М1(a, b) и М2(c, d), которая расположена ближе к началу координат.
2. Даны уравнения прямых а₁х+b₁y=c₁, a₂x+b₂y=c₂, a₃x+b₃y=c₃. Выяснить, какие из этих прямых перпендикулярны или указать, если таковых не имеется.
3. Составить программу определения минимального элемента из трех элементов х1, х2, х3.
4. Составить программу вычисления значения функции
   

Вариант 16.

1. Дано вещественное x. Составить алгоритм вычисления f(x), если .

Пpедусмотpеть pазpешение аваpийных ситуаций.

2. Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения:

3. Арифметические действия над числами пронумерованы следующим образом: 1 — сложение, 2 — вычитание, 3 — умножение, 4 — деление. Дан номер действия N (целое число в диапазоне 1–4) и вещественные числа A и B (В не равно 0). Выполнить над числами указанное действие и вывести результат.

4. Дано целое число, лежащее в диапазоне 1–999. Вывести его строку-описание вида «четное двузначное число», «нечетное трехзначное число» и т. д.

Вариант 17.

1. Дано вещественное x. Составить алгоритм вычисления f(x), если . Пpедусмотpеть pазpешение аваpийных ситуаций.

2. Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения:

3. Дан номер года (положительное целое число). Определить количество дней в этом году, учитывая, что обычный год насчитывает 365 дней, а високосный — 366 дней. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400 (например, годы 300, 1300 и 1900 не являются високосными, а 1200 и 2000 — являются).

4. Даны два целых числа: D (день) и M (месяц), определяющие правильную дату. Вывести знак Зодиака, соответствующий этой дате: «Водолей» (20.1–18.2), «Рыбы» (19.2–20.3), «Овен» (21.3–19.4), «Телец» (20.4–20.5), «Близнецы» (21.5–21.6), «Рак» (22.6–22.7), «Лев» (23.7–22.8), «Дева» (23.8–22.9), «Весы» (23.9–22.10), «Скорпион» (23.10–22.11), «Стрелец» (23.11–21.12), «Козерог» (22.12–19.1).

 

 

Вариант 18.

1. Дано вещественное x. Составить алгоритм вычисления f(x), если 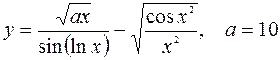. Пpедусмотpеть pазpешение аваpийных ситуаций.
2. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения. Вывести новые значения переменных A и B.
3. Робот может перемещаться в четырех направлениях («С» — север, «З» — запад, «Ю» — юг, «В» — восток) и принимать три цифровые команды: 0 — продолжать движение, 1 — поворот налево, –1 — поворот направо. Дан символ C — исходное направление робота и целое число N — посланная ему команда. Вывести направление робота после выполнения полученной команды.
4. Составить алгоритм нахождения номера N четверти координатной плоскости, которой принадлежит заданная точка (x,y), где .

Вариант 19.

1. Дано вещественное x. Составить алгоритм вычисления f(x), если 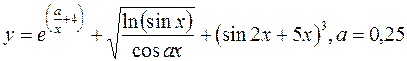. Пpедусмотpеть pазpешение аваpийных ситуаций.

2. Даны четыре целых числа, одно из которых отлично от трех других, равных между собой. Определить порядковый номер числа, отличного от остальных.

3. В восточном календаре принят 60-летний цикл, состоящий из 12-летних подциклов, обозначаемых названиями цвета: зеленый, красный, желтый, белый и черный. В каждом подцикле годы носят названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. По номеру года определить его название, если 1984 год — начало цикла: «год зеленой крысы».

4.

Дано вещественное x. Составить алгоритм вычисления f(x), если f(x) задана графически

Вариант 20.

1. Дано вещественное x. Составить алгоритм вычисления f(x), если . Пpедусмотpеть pазpешение аваpийных ситуаций.
2. 
   Дано вещественное x. Составить пpогpамму вычисления f(x), если f(x) задана графически

3. Даны три числа. Найти сумму двух наибольших из них.

4. Мастям игральных карт присвоены порядковые номера: 1 — пики, 2 — трефы, 3 — бубны, 4 — червы. Достоинству карт, старших десятки, присвоены номера: 11 — валет, 12 — дама, 13 — король, 14 — туз. Даны два целых числа: N — достоинство (6 £ N £ 14) и M — масть карты (1 £ M £ 4). Вывести название соответствующей карты вида «шестерка бубен», «дама червей», «туз треф» и т. п.

Поделиться:

Воспользуйтесь поиском по сайту: