 |
Вычисление количества информации какого то определенного частного случая
|
|
|
|
ВЕРОЯТНОСТНЫЙ ПОДХОД К ИЗМЕРЕНИЮ КОЛИЧЕСТВА ИНФОРМАЦИИ
РАВНОВЕРОЯТНОСТНЫЕ СОБЫТИЯ
Вероятностный подход связан с таким понятием как ВЕРОЯТНОСТЬ.
ВЕРОЯТНОСТЬ — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов.
Вероятность обозначают буквой p.
(где K — количество тех наблюдений, при которых рассматриваемое событие наступило, N — общее количество наблюдений)
За 1 бит информации принимают такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных.
Бит — это количество информации, уменьшающее неопределенность знаний в два раза.
При РАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности наступления того или иного события равны.
Для измерения количества информации, полученной нами при равновероятном событии, используем формулу
( где N — количество возможных исходов события,
i — количество информации, которое мы получим, при том или ином исходе события)
Пример: Мы подбрасываем монетку. В большинстве своих случаев (не учитывает ребро) она может упасть либо на ОРЕЛ, либо на РЕШКУ. Вероятность наступления данных событий равны (50\50) — т.е. это равновероятностный подход. 2 равновероятных события. Таким образом: 2=2i. i=1 биту. Это то количество информации, которое мы получим, когда монетка упадет, и мы узнаем, на какую сторона выпала (орел или решка).
Пример: В книге 512 страниц. Сколько информации несет сообщение о том, что закладка лежит на какой-либо странице?
Решение
N=512; 2i = N
i-? 2i=512
i=9
Пример: Сколько информации содержит сообщение о выпадении грани с числом 3 на шестигранном игральном кубике?
|
|
|
Решение
N=6 2i = N
i-? 2i=6
i ≈ 2,5
Ответ: 2,5 бит
НЕРАВНОВЕРОЯТНОСТНЫЕ СОБЫТИЯ
Логари́фм числа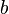 
по основанию 
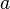определяется как показатель степени, в которую надо возвести основание 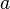, чтобы получить число .
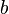Обозначение: 
, произносится: «логарифм 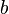по основанию ».
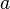Из определения следует, что нахождение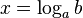 
равносильно решению уравнения 
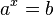. Например, 
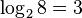, потому что 
.
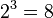Свойства логарифмов:
1. 
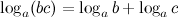- логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
2. 
- логарифм частного.
ВЫЧИСЛЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ КАКОГО ТО ОПРЕДЕЛЕННОГО ЧАСТНОГО СЛУЧАЯ
Для вычисления количества информации в сообщении о неравновероятном событии (частного случая) используют следующую формулу: I=log2(1/p)
где I – это количество информации, р – вероятность события.
Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,
где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса.
Пример: В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти. Сколько информации несет сообщение, что достали клубок красной шерсти?
Дано: Кк=4;N=32
Найти: Iк
Решение:
1. Найдем вероятность доставания клубка красной шерсти: pк= Кк/N=4/32=1/8;
2. Найдем количество информации, которое несет сообщение, что достали клубок красной шерсти: Iк= log2(1/ pк)= log2(1/1/8)= log28=3 бит
Ответ: Iк=3 бит;
Пример: В корзине лежат белые и черные шары. Среди них 30 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Какова вероятность выпадения черного шара? Сколько всего в корзине шаров?
Решение:
1. Найдем вероятность выпадения белого шара:
Iб= log2(1/ pб);
2= log2(1/ pб);
22=1/ pб ;
4= 1/ pб ;
pб = ¼.
2. Найдем вероятность выпадения черного шара. Нам известно, что сумма всех вероятностей всегда равняется 1. В нашей задаче может произойти всего два события: либо выпадет белый шарик, либо черный, соответственно pб + pч = 1, следовательно, pч = 1- pб =3/4
|
|
|
3. Найдем количество шариков в корзине. Нам известно по общей формуле, что р= k/N. Применительно к нашему случаю pч = kч/N. Подставляем известные значения в нашу формулу.
¾ = 30/N;
3N= 120;
N= 40.
Ответ: pч =3/4; N= 40
|
|
|
