Каноническая запись итерационных процессов.

Лекция №14

Итерационные методы решения СЛАУ

Методы решения уравнения Пуассона.

Метод простых итераций.

Рассмотрим итерационный метод (т.е. метод последовательных приближений) решения системы линейных уравнений:

(1)

Будем считать, что решение задачи (1) существует и единственно. Различные варианты метода простых итераций связаны с переходом от системы (1) к эквивалентной системе

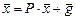
(2)

Итерационный процесс строим следующим образом:

,

(3)

где 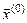- начальное приближение, - номер приближения.

Укажем условия сходимости метода последовательных приближений (3).

Теорема 1. Для сходимости итераций (3) к решению системы (2) достаточно, чтобы в какой‑либо норме выполнялось условие . Тогда независимо от выбора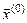

,

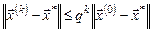(4)

где 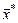- точное решение системы (2).

Доказательство

При подстановке точного решения в (2) оно обращается в тождество:

.

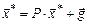Вычитая его из уравнения (3), (т.е. ), получим:

.

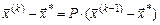Здесь - погрешность 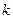-го приближения.

Оценивая погрешность по какой‑либо норме (с которой согласована норма матрицы), получим:

Ясно, что при .

Теорема 2. (без доказательства) Для сходимости итерационного процесса (3) к решению системы (2) необходимо и достаточно, чтобы все собственные значения матрицы по абсолютной величине были меньше единицы.

Опираясь на формулу (4), можно получить априорную оценку числа приближений

.

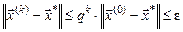Разрешая последнее неравенство относительно 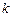, получим:

.

(Квадратные скобки означают ближайшее сверху целое число от того, которое заключено в скобки). Этой оценкой можно воспользоваться, если мажорировать .

Упражнение. Показать, что в условиях Теоремы 1 справедлива оценка:

.

Задумаемся о том, зачем нужны итерационные методы, если мы можем найти решение, пользуясь, например, какой‑либо модификацией метода Гаусса. Ответ на это вопрос становиться понятным, если оценить эффективность различных подходов с точки зрения вычислительных затрат.

Метод Гаусса (в простейшей интерпретации), при требует выполнения приблизительно арифметических операций.

Метод итераций реализуется приблизительно за операций ( умножений и сложений связано с умножением матрицы на вектор 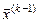, 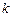- число приближений). Если допустимая погрешность достигается при , то метод итераций становиться предпочтительней.

Замечание. В практических задачах, как правило, .

Кроме того, методы итераций могут оказаться предпочтительней с точки зрения устойчивости вычислений, т.е. в смысле влияния вычислительных погрешностей на результаты расчетов.

Метод Якоби.

Запишем каждое уравнение системы в виде, разрешенном относительно неизвестного с коэффициентом на главной диагонали матрицы :

, .

Таким образом, мы переписали в виде , с матрицей

Введём в рассмотрение диагональную матрицу:

,

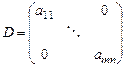то

,
.

Действительно, , где - алгебраическое дополнение к элементу , поэтому

,
,
.

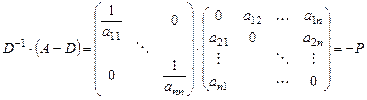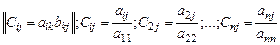Итерационный процесс, определенный такой матрицей , называется методом Якоби. Фактически вычисления проводятся по формулам

, .

Утверждение. Для сходимости метода Якоби достаточно, чтобы для исходной матрицы A имело место диагональное преобладание, т.е. чтобы

.

В самом деле, тогда условие теоремы 1 выполнено для нормы :

.

 

Пусть теперь дано двумерное уравнение Пуассона в прямоугольнике

, .

Выбирая для простоты сетку, равномерную и одинаковую по и , получим пятиточечный шаблон (Рис. 1):

Рис. 1. Пятиточечный шаблон

Тогда в узле получим:

.
,

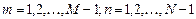
Итерационный процесс Якоби здесь реализуется следующим образом:

1. Значения функции на границе заданы, известны;

2. Зададим некоторое начальное приближение функции во внутренних узлах (близость этого значения к решению часто бывает очень важна);

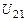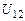3. Вычисляем по окружающим точкам нулевого приближения: и на границе, а также и ;

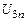4. Затем по , и , и т.д. до , затем по аналогии и т.д

После последовательного прохождения по всем линиям от 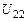до , от до , , до один цикл итераций выполнен. Число арифметических операций на шаге равно .

Ясно, что при вычислении удобно воспользоваться уже известным значением с первого шага итерации. В этом случае погрешность предыдущей итерации последовательно оттесняется слева направо и снизу вверх. Такая модификация итерационного процесса называется методом Зейделя.

Метода Зейделя

Формулы метода Зейделя имеют вид:

,
,
.

Если представить матрицу в виде суммы ( - нижняя треугольная, верхняя треугольная и диагональная матрицы с элементами матрицы ), то методу Зейделя соответствует матрица:

(для метода Якоби ). Можно доказать, что метод Зейделя гарантированно сходится, если выполнено условие диагонального преобладания матрицы A или матрица является симметричной (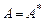) и положительно определенной.

В одинаковых условиях (диагональное преобладание) метод Зейделя сходится примерно в два раза быстрее метода Якоби (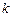 итераций и итераций). Для оценки сходимости итерационных методов часто используются модельные (тестовые) задачи.

При решении пятиточечного уравнения Пуассона (схема “Крест”), возможна реализация не точечного, а “блочного” метода Зейделя. В этом случае уравнения записываются в виде:

при :

,

(*)

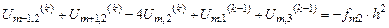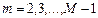
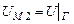При этом заданы и - граничные условия.

Система 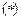решается методом прогонки (что можно сделать для любых граничных условий, а не только первого рода), и системе сеточных функций присваивается новое значение “ 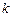- той итерации”.

Затем решается система уравнений при :

,

с граничными условиями справа и слева. При этом берется с уже посчитанного уравнения на линии , а - с предыдущей итерации. Таким образом, погрешность (невязка) “блочно”, линиями оттесняется “снизу вверх”.

После проведения первой итерации по строкам (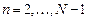) эффективно выполнить первую итерацию с прогонками по столбцам (). Таким образом, происходит “утрясание” как в “решете” с фиксированными граничными условиями на краях.

В случае граничных условий 2 или 3 рода (Рис. 2) сходимость итерационного процесса резко замедляется по вполне понятным причинам.

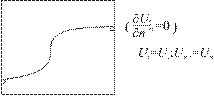
Рис. 2. Граничные условия 2 или 3-го рода.

 

Каноническая запись итерационных процессов.

Для решения различных линейных схем множество итерационных схем можно записать в канонической форме:

- в этом случае это явные итерационные процессы,

- неявные итерационные процессы,

- стационарные итерационные процессы.

Мы рассмотрели:

1) 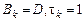- метод Якоби.

2) - метод Зейделя.

 

Чтобы ускорить итерационный процесс, видоизменяют метод Зейделя, вводя итерационный параметр так, чтобы

.

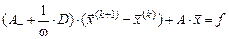Такой метод называется методом релаксации. Метод Зейделя соответствует значению . Если , то итерационный процесс называется методом верхней релаксации. Здесь

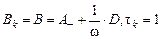
стационарный неявный итерационный процесс.

Условия сходимост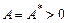и: и .

Скорость сходимости зависит от параметра . Существуют теоретические оценки для и скорости сходимости, но их применение требует знания спектра оператора , который не всегда легко найти. Поэтому на практике параметр подбирают так, чтобы минимизировать число итераций. Это особенно удобно, если решается класс однотипных задач.

Для примера рассмотрим применение метода верхней релаксации в одной сложной численной схеме (нелинейные уравнения Навье - Стокса), где на каждом шаге по времени необходимо решать эллиптическое уравнение Пуассона

, ,

с граничными условиями первого рода. Запишем разностную схему в виде:

, .

В данном случае используются цилиндрические координаты и неравномерная сетка, но это приводит лишь к появлению зависящих от индекса и прогоночных коэффициентов. Скорость сходимости процесса сильно зависит от нулевого начального приближения, за которое принято значение на прошлом шаге по времени.

Сначала, как и в методе Зейделя, выполняются прогонки по строкам от до 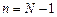. Вторая часть итерации состоит в выполнении прогонок по столбцам. Выполняя прогонку при (), вычисляем новое значение , но в ячейки заносим не это значение, а значение

.

При 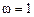- это блочный метод Зейделя.

При берется с некоторым “весом” предыдущей итерации. (Например, при : - запаздывание).

При берется с избыточным “весом” с новой - той итерации. (Например, при : )

Предположим, необходима относительная точность вычислений:

,
.

На первых шагах итераций берется , затем, когда наступает условие , значение меняется на 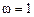, а когда или , то можно взять , и итерации быстро сходятся до .

 

Поделиться:

Воспользуйтесь поиском по сайту: