 |
Методические указания к выполнению РГР
|
|
|
|
«Расчет характеристик и оптимизация сетевого графика выполнения проекта»
по дисциплине Математические методы сетевого планирования
Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме их выполнения приведены в следующей таблице:
| Имя работы | A | B | C | D | E |
| Опирается на работу | C, G | E, F | A, H | A, H | |
| Нормальный срок (дни) | |||||
| Ускоренный срок (дни) | |||||
| Норм. стоим. (млн. р.) | |||||
| Плата за ускор. (млн. р.) |
| Имя работы | F | G | H | K | L |
| Опирается на работу | C, G | L | L | ||
| Нормальный срок (дни) | |||||
| Ускоренный срок (дни) | |||||
| Норм. стоим. (млн. р.) | |||||
| Плата за ускор. (млн. р.) |
Требуется:
1. С учетом технологической последовательности работ построить сетевой график выполнения этих работ.
2. Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ. Найти критический путь и его продолжительность, указать все возможные критические пути, определить стоимость всего комплекса работ.
3. Указать стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 4 дня. В какую итоговую сумму обойдется фирме ускоренная стройка павильона?
Прежде, чем приступить к решению сформулированной задачи, рассмотрим некоторые понятия теории сетевого планирования и управления.
|
|
|
Аппарат сетевого планирования и управления (сокращенно СПУ) - это совокупность моделей и методов планирования и управления выполнением комплекса работ, в основе которых лежит понятие сетевого графика или сетевой модели. Под комплексом работ понимается любая задача или проблема, для решения которой необходимо выполнить достаточно большое количество разнообразных работ. Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ, заданный в специфической форме сети, графическое изображение которой называют сетевым графиком.
Модели и методы СПУ предназначены для решения двух основных проблем:
* формирование календарного плана реализации комплекса работ;
* принятие эффективных решений в процессе выполнения этого плана.
Главными элементами сетевой модели являются события и работы. Событие - это момент достижения некоторого результата. Событие не имеет протяженности во времени. Понятие “ работа ” может иметь в СПУ разный смысл и обозначать:
* действительную работу, требующую затрат времени и ресурсов;
* ожидание, не требующее затрат ресурсов, но занимающее определенное время;
* фиктивную работу, которая вводится для отображения логической связи между событиями, не требует затрат ресурсов и не имеет продолжительности во времени.
Для каждой работы сетевой модели должны быть определены такие работы, на результаты которых она непосредственно опирается и которые должны быть завершены к моменту начала выполнения рассматриваемой работы. На сетевом графике, т.е. графическом изображении сетевой модели, события изображаются кружками, а работы - стрелками.
Среди событий сетевой модели выделяют начальное и конечное. Начальное событие не имеет предшествующих работ, а конечное - последующих работ. Начало работы и ее завершение являются событиями, называемыми соответственно начальным и конечным событием данной работы. Для обозначения событий обычно используются порядковые числа: 1, 2, 3,...; для обозначения работ используются либо буквы - А, В, С,..., либо пары числе - (i, j), где i - номер начального события, j - номер конечного события для данной работы.
|
|
|
При построении сетевого графика следует основываться на следующих правилах:
1. В сетевом графике должно быть одно начальное и одно конечное событие. На рис. 4.1 а) изображен график, не удовлетворяющий этому правилу, а на рис. 4.1 б) показано, каким образом его можно преобразовать, чтобы обеспечить выполнение первого правила.
 |
а) б)
Рис. 4.1. Иллюстрация первого правила построения сетевых графиков.
2. В сетевом графике не должно быть замкнутых контуров (изображен на рис. 4.2 а). При возникновении такой ситуации следует еще раз изучить исходные данные и путем пересмотра состава работ и (или) логических связей между ними добиться устранения замкнутого контура в сетевом графике.
3. Любые два события в сетевом графике могут быть непосредственно связаны не более, чем одной работой.
 На рис. 4.2 б) изображен фрагмент сетевого графика, не удовлетворяющий этому правилу, а на рис. 4.2 в) показано, как можно устранить такую ситуацию
На рис. 4.2 б) изображен фрагмент сетевого графика, не удовлетворяющий этому правилу, а на рис. 4.2 в) показано, как можно устранить такую ситуацию
а) б) в)
Рис. 4.2 Иллюстрация второго и третьего правил построения сетевого графика
4.1. Построение сетевого графика выполнения комплекса работ
Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. В нашей задаче такими работами являются С, H, L. По определению, момент завершения работы является событием. Поэтому каждая стрелка, соответствующая работам C, H, L, завершается кружком - событием, в котором проставляется номер этого события. Нумерация событий - произвольная. Описанные построения изображены на рис. 4.3.
 |
Рис. 4.3. Первый этап построения сетевого графика
На следующем этапе построения сетевого графика изображаем работы, которым предшествуют C, H, L, или, что то же самое, которые опираются на C, H, L. Просматривая список работ, видим, что на работу C опираются работы А и F. Поэтому из события 2 выпускаем стрелки, соответствующие работам А и F. Аналогичным образом поступаем с работами H и L: на H опираются D и E, а на L опираются G и К. Этот этап построения сетевого графика изображен на рис. 4.4.
|
|
|
 |
Рис. 4.4. Второй этап построения сетевого графика
Заметим, что на данном этапе работы A, F,..., K пока не завершены событиями. Связано это с тем, что конечными событиями для этих работ могут оказаться какие-то из уже обозначенных событий 2, 3, 4.
На следующем этапе построения сетевого графика изображаем те работы, которые опираются на A, F, D, E, G, K, и изображаем пока еще не отраженные логические взаимосвязи между работами. Начинаем с работы А. Из списка работ видно, что на А опираются D и Е. Следовательно, стрелку, изображающую работу А следует направить в событие 3, которое является начальным для работ D и Е.
Далее, на F опирается одна работа В, которая еще не была изображена на сетевом графике. Следовательно, работу F завершает событие 5, из которого выпускаем стрелку, соответствующую работе В.
На работу D не опираются какие-либо работы. Следовательно, D является одной из завершающих работ, и конечное событие этой работы совпадает с конечным событием всего комплекса работ. Обозначаем конечное событие сетевого графика цифрой 6, и в кружок с этой цифрой проводим стрелку, соответствующую работе D.
На работу Е опирается работа В. Следовательно, стрелку - работу Е проводим к событию 5, из которого выходит стрелка - работа В.
На G опираются A и F. Поскольку начальным событием для A и F является событие 2, то это событие будет конечным для G. Поэтому стрелку, изображающую G, проводим к событию 2. Наконец, на К не опираются никакие работы. Следовательно, конечным событием для К будет конечное событие сетевого графика 6. Поэтому стрелку - работу К проводим к событию 6, и третий этап построения сетевого графика завершен.
Последним, четвертым этапом построения сетевого графика рассматриваемой задачи будет этап, на котором выявляются и изображаются на графике логические взаимосвязи работы В с другими работами. Из списка работ видно, что на В не опираются какие-либо работы. Следовательно, она является одной из завершающих. Поэтому стрелку - работу В проводим в конечное событие 6. Два заключительных этапа построения сетевого графика изображены на рис. 4.5.
|
|
|
 |
Рис. 4.5. Заключительные этапы построения сетевого графика
 В построенном сетевом графике 4-е событие предшествует 2-му событию. Очевидно, что сетевой график выглядит более естественно, если номера предшествующих событий меньше номеров последующих событий. Рассмотрим простой метод упорядочения сетевого графика, который позволяет путем перенумерации событий добиться того, чтобы все последующие события имели большие номера, чем предшествующие события. Этот метод основан на понятии ранга события. Все события сетевого графика подразделяются на ранги. К одному рангу может относиться несколько событий. Нумерация событий производится в соответствии с принадлежностью к тому или иному рангу. Чем выше ранг, тем больший номер имеет событие. Внутри одного ранга нумерация событий произвольна.
В построенном сетевом графике 4-е событие предшествует 2-му событию. Очевидно, что сетевой график выглядит более естественно, если номера предшествующих событий меньше номеров последующих событий. Рассмотрим простой метод упорядочения сетевого графика, который позволяет путем перенумерации событий добиться того, чтобы все последующие события имели большие номера, чем предшествующие события. Этот метод основан на понятии ранга события. Все события сетевого графика подразделяются на ранги. К одному рангу может относиться несколько событий. Нумерация событий производится в соответствии с принадлежностью к тому или иному рангу. Чем выше ранг, тем больший номер имеет событие. Внутри одного ранга нумерация событий произвольна.
Проведем упорядочение построенного сетевого графика. Начальное событие относим к нулевому рангу и перечеркиваем одной чертой все стрелки - работы, выходящие из этого события, т.е. стрелки, обозначающие работы C, H, L. К первому рангу относим те события, которые не имеют входящих неперечеркнутых стрелок - работ (см. рис. 4.6 а). Таким событием будет одно - 4-е. Далее, перечеркиваем двумя чертами работы - стрелки, выходящие из событий 1-го ранга, т.е. из 4-го события (см. рис. 4.6 а). Ко второму рангу относим те события, которые не имеют входящих неперечеркнутых стрелок. Таким будет единственное событие 2. Описанная процедура вычеркивания стрелок - работ изображена на рис. 4.6 а).
 |
а) б)
Рис. 4.6. Упорядочение сетевого графика
Продолжая описанный процесс упорядочения, который изображен на рис. 4.6 б), получим
* к третьему рангу относится событие 3,
* к четвертому - событие 5,
* к пятому - событие 6.
Результат проделанного упорядочения можно представить следующей таблицей 1.
Таблица 1
| Номер ранга | ||||||
| Первоначальные номера событий | ||||||
| Новые номера событий |
Упорядоченный сетевой график строительства торгового павильона изображен на рис. 4.7, где рядом с буквой, обозначающей работу, в скобках проставлено число, равное нормальному сроку ее выполнения.
 |
|
|
|
Рис. 4.7. Сетевой график строительства торгового павильона
4.2. Расчет временных характеристик сетевого графика. Нахождение критического пути
Одним из важнейших понятий сетевого графика является понятие пути. Путь - это любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Полный путь - это путь от начального до конечного события сетевого графика. Например, в построенном сетевом графике строительства торгового павильона последовательности работ P1 = (L, G, A); P2 = (A, D) образуют пути, а последовательности P3 = (C, F, B); P4 = (L, K) образуют полные пути. Продолжительность или длительность выполнения работ будем обозначать буквой “ t ” с индексом наименования работы. Так, t A - длительность выполнения работы A. При расчете временных характеристик сетевого графика продолжительность выполнения работ удобнее обозначать через t ij, где i - номер начального, а j - номер конечного события данной работы. Например, t A º t 34 = 10, t C º t 13 = 29. Сумма продолжительностей работ, составляющих путь P, выражает продолжительность или длину всего пути, и обозначается через t(P). Например
t (P1) = t L + t G + t A º t 12 + t 23 + t 34 = 10 + 10 +10 = 30;
t (P3) = t C + t F + t B º t 13 + t 35 + t 56 = 29 + 20 + 12 = 61.
Полный путь, имеющий наибольшую продолжительность, называется критическим путем, а длина критического пути называется критическим временем или критическим сроком сетевого графика и обозначается через Tкр. Критическое время - это наименьшее время выполнения всего комплекса работ. Сетевой график может иметь несколько различных критических путей, но все они, очевидно, должны иметь одну и ту же длину.
Критические пути, вообще говоря, могут быть найдены путем перебора всех полных путей. Однако, в сетевой модели, содержащей достаточно много работ, полных путей может оказаться столько, что на их перебор не хватит никакого времени. Существует простой алгоритм нахождения критического пути и критического времени, основанный на понятии раннего времени наступления события. Раннее время наступления i -го события (обозначается  ) - это момент времени, раньше которого событие i не может наступить. Каждое событие может наступить только тогда, когда будут выполнены все работы на всех путях, ведущих от начального события графика к данному событию. Поэтому раннее время
) - это момент времени, раньше которого событие i не может наступить. Каждое событие может наступить только тогда, когда будут выполнены все работы на всех путях, ведущих от начального события графика к данному событию. Поэтому раннее время  наступления i -го события равно наибольшей длине путей, ведущих от начального события к i -му событию.
наступления i -го события равно наибольшей длине путей, ведущих от начального события к i -му событию.
Рассчитаем  для всех событий сетевого графика, т.е. для i = 1, 2,..., 6. Время наступления 1-го, начального, события сетевого графика будем считать равным нулю, т.е.
для всех событий сетевого графика, т.е. для i = 1, 2,..., 6. Время наступления 1-го, начального, события сетевого графика будем считать равным нулю, т.е.  . Далее последовательно находим
. Далее последовательно находим  ,...,
,...,  . Так как событие 2 наступает сразу после выполнения работы L, “выходящей” из начального события, то раннее время наступления 2-го события будет равно времени выполнения работы L. Поскольку t L = t 12 = 10, то
. Так как событие 2 наступает сразу после выполнения работы L, “выходящей” из начального события, то раннее время наступления 2-го события будет равно времени выполнения работы L. Поскольку t L = t 12 = 10, то  = t 12 = 10.
= t 12 = 10.
Далее определяем раннее время наступления 3-го события, к которому от начального ведут два пути, состоящие из работ C (первый путь) и L, G (второй путь). Следовательно, по определению раннего времени наступления события, 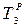 = max { t c, t L + t G} = max { t 13, t 12 + t 23} = max {29, 10 + 10} = 29.
= max { t c, t L + t G} = max { t 13, t 12 + t 23} = max {29, 10 + 10} = 29.
Если находить  исходя из определения, т.е. как наибольшую продолжительность путей, ведущих от начального события к i -му, то, с одной стороны, нам придется выявлять все эти пути, а, с другой стороны, по мере увеличения i количество таких путей будет очень быстро возрастать и, следовательно, нахождение
исходя из определения, т.е. как наибольшую продолжительность путей, ведущих от начального события к i -му, то, с одной стороны, нам придется выявлять все эти пути, а, с другой стороны, по мере увеличения i количество таких путей будет очень быстро возрастать и, следовательно, нахождение  превратится в громоздкую и трудоемкую процедуру. Оказывается, этого можно избежать, используя найденные
превратится в громоздкую и трудоемкую процедуру. Оказывается, этого можно избежать, используя найденные  для k -х событий, наступивших раньше i -го события. Действительно, 3-е событие не может наступить раньше, чем:
для k -х событий, наступивших раньше i -го события. Действительно, 3-е событие не может наступить раньше, чем:
* будет выполнена работа C,
* будет выполнена работа G, которую можно начать выполнять только после наступления 2-го события. Следовательно,
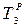 = max{
= max{  + t C,
+ t C,  + t G} = max{
+ t G} = max{  + t 13,
+ t 13,  + t 23} = max{0+29, 10+10} = 29.
+ t 23} = max{0+29, 10+10} = 29.
Аналогично,
 = max{
= max{  + t H,
+ t H, 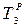 + t A} = max{
+ t A} = max{  + t 14,
+ t 14, 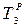 + t 34} = max{0+18, 29+10}= 39,
+ t 34} = max{0+18, 29+10}= 39,
 = max{
= max{ 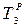 + t 35,
+ t 35,  + t 45} = max{29+20, 39+10}= 49,
+ t 45} = max{29+20, 39+10}= 49,
 = max{
= max{  + t 26,
+ t 26,  + t 46,
+ t 46,  + t 56} = max{10+37, 39+19, 49+12}=
+ t 56} = max{10+37, 39+19, 49+12}=
= max{47, 58, 61}=61.
Таким образом, раннее время наступления конечного события сетевого графика составляет 61 день, т.е. раньше, чем за 61 день, торговый павильон не может быть построен. Следовательно Ткр =  = 61.
= 61.
Алгоритм нахождения критического пути, который обозначим через Pкр, состоит в следующем. Рассмотрим формулу, из которой было найдено критическое время Т кр =  = max{
= max{  + t 26,
+ t 26,  + t 46,
+ t 46,  + t 56} =
+ t 56} =  + t 56 = 61, и определим работу, на которой был достигнут максимум в этой формуле. Очевидно, что это работа (5, 6), т.е. В. Работа В является критической, т.е. принадлежит критическому пути. Далее рассматриваем раннее время наступления того события, которое является начальным для работы В, т.е. рассматриваем
+ t 56 = 61, и определим работу, на которой был достигнут максимум в этой формуле. Очевидно, что это работа (5, 6), т.е. В. Работа В является критической, т.е. принадлежит критическому пути. Далее рассматриваем раннее время наступления того события, которое является начальным для работы В, т.е. рассматриваем  = max{
= max{ 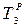 + t 35,
+ t 35,  + t 45} =
+ t 45} =  = 49.
= 49.
Поскольку максимум достигается на двух работах (3, 5) и (4, 5), то обе эти работы являются критическими, т.е. F и E - критические работы. Следовательно, данный сетевой график имеет по крайней мере два критических пути.
Продолжим нахождение критических работ того пути, который содержит работу F. Так как 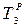 = max{
= max{  + t 13,
+ t 13,  + t 23} =
+ t 23} =  + t 13, то работа (1, 3) т.е. работа С, является критической. Поскольку работе С не предшествуют какие-либо работы, то нахождение первого критического пути завершено и
+ t 13, то работа (1, 3) т.е. работа С, является критической. Поскольку работе С не предшествуют какие-либо работы, то нахождение первого критического пути завершено и  = (С, F, B).
= (С, F, B).
Теперь найдем критический путь, содержащий работу Е, т.е. работу (4, 5). Так как  = max{
= max{  + t 14,
+ t 14, 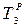 + t 34} =
+ t 34} =  + t 34, то работа (3, 4), т.е. работа А, является критической. Поскольку
+ t 34, то работа (3, 4), т.е. работа А, является критической. Поскольку 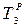 = max{
= max{  + t 13,
+ t 13,  + t 23} =
+ t 23} =  + t 13, то работа (1, 3), т.е. работа С, является критической. Таким образом, найден второй критический путь, и
+ t 13, то работа (1, 3), т.е. работа С, является критической. Таким образом, найден второй критический путь, и  = (С, А, E, B). На рис. 4.8 критические пути выделены двойными стрелками.
= (С, А, E, B). На рис. 4.8 критические пути выделены двойными стрелками.
 |
Рис. 4.8. Сетевой график с критическими путями
Стоимость S строительства торгового павильона определяется как сумма стоимостей выполнения всех работ при нормальном сроке выполнения каждой:
S = 26 + 32 + 40 + 43 + 26 + 45 + 26 + 41 + 68 + 26 = 373 (тыс. руб.)
Таким образом получены следующие результаты решения задачи 4.2:
* критический срок Ткр = 61;
* критические пути  = (С, F, B);
= (С, F, B);  = (С, А, E, B);
= (С, А, E, B);
* стоимость строительства в нормальном режиме S = 373 тыс. руб.
4.3. Сокращение срока строительства торгового павильона
По условию задачи необходимо сократить период строительства на 4 дня, т.е. вместо 61 дня построить павильон за 57 дней, и добиться этого с минимальными дополнительными затратами. Сокращение срока строительства может быть обеспечено только путем сокращения сроков выполнения работ, принадлежащих критическому пути, а сокращение срока выполнения любой работы требует дополнительных затрат. Для разных работ дополнительные затраты на ускорение различаются. Поэтому, сокращая время выполнения тех критических работ, которые требуют наименьших дополнительных затрат, можно добиться минимального удорожания всего комплекса работ.
Будем предполагать, что затраты на ускорение выполнения каждой работы прямо пропорциональны периоду ускорения, т.е. если, например, для работы В плата за ускорение составляет 6 тыс. руб., а максимальное ускорение этой работы составляет 2 дня, то каждый день сокращения приводит к дополнительным затратам в 6/2 = 3 (тыс. руб.). Исходные данные о сроках и рассчитанные значения удельных затрат сокращения выполнения каждой работы занесем в табл. 2.
Таблица 2
| Работы | A | B | C | D | E | F | G | H | K | L |
| Максимальное сокращение времени выполнения (дн.) | ||||||||||
| Удельные затраты на ускорение (тыс. руб./дн.) |
Как отмечалось выше, уменьшение периода строительства может быть достигнуто только за счет ускорения выполнения критических работ. Но ускорение критических работ может привести к тому, что на сетевом графике возникнут другие критические пути, отличные от уже выявленных.
Если мы не заметим появления новых критических путей, то может возникнуть ситуация, в которой сокращение продолжительности работ, лежащих на “старых” критических путях, не приведет к сокращению продолжительности выполнения всего комплекса, так как период строительства павильона будет определяться критическим временем новых критических путей. Поэтому, сокращая время выполнения критических работ, необходимо отслеживать появление новых критических путей. Если такие пути появляются, то следует так сокращать время выполнения работ, чтобы продолжительность каждого критического пути уменьшилась на одно и то же количество дней.
Отследить появление новых критических путей можно, например, следующим способом - на каждом этапе сокращения критических работ просматривать и анализировать все полные пути сетевого графика. Для построенного сетевого графика строительства торгового павильона все полные пути изображены на рис. 4.9, где справа от цепочки работ каждого полного пути указана его продолжительность. Найденным ранее критическим путям соответствуют полные пути P5 и P7.
Просматривая все полные некритические пути, убеждаемся, что при сокращении срока строительства на 4 дня, т.е. до 57 дней, критическим может стать только путь P6, поскольку все остальные полные пути имеют продолжительность до 52 дней. Поэтому, сокращая критические работы, будем следить за изменением продолжительности только пути P6.
 | ||||
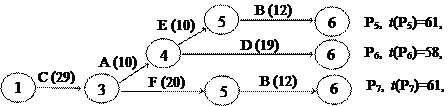 | ||||
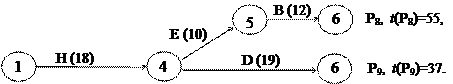 |
Рис. 4.9. Полные пути сетевого графика
При уменьшении срока выполнения всего комплекса работ с минимальным удорожанием необходимо учитывать:
* возможные сроки сокращения критических работ;
* удельные стоимости удорожания работ;
* принадлежность одной и той же работы к разным критическим путям.
Единовременно, т.е. за один шаг, сократить критический срок на требуемое количество дней, как правило, не удается, так как при таком сокращении могут появиться новые критические пути, критическое время которых окажется больше полученного нами в результате единовременного сокращения. Самый надежный способ состоит в последовательном сокращении критического времени на один день на каждом шаге. Однако, применение этого способа не является обязательным, т.е., вообще говоря, за один шаг можно сокращать критическое время на 2, 3 и более дней. Выбор количества дней, на которые следует сокращать критическое время за один шаг зависит от структуры конкретного сетевого графика.
Рассмотрим критические пути P5 и P7. Им принадлежат две общие работы В и С с резервами для сокращения в 2 дня для каждой. Удельные затраты на ускорение составляют 4 тыс. руб./день для работы С и 3 тыс. руб./день для работы В. Следовательно, выгоднее сокращать время выполнения работы В. При этом дополнительные затраты составят
2 (дня) ´ 3 (тыс. руб./день) = 6 (тыс. руб.),
критическое время Ткр станет равным
Ткр = 61 (день) - 2 (дня) = 59 (дней),
новых критических путей не появляется.
На рис. 4.10 изображены полные пути P5, P6, P7 с сокращенным временем выполнения работы В.
 |
Рис. 4.10. Иллюстрация первого шага оптимизации сетевого графика
Заметим, что существует еще один вариант сокращения критического времени на 2 дня:
* на пути P5 сокращаем работы А и Е на один день каждую,
* на пути P7 сокращаем работу F на два дня.
Дополнительные затраты при этом составят:
для пути P5: 1 (день) ´ 2 (тыс. руб./день) + 1 (день) ´ 2 (тыс. руб./день) = 4 (тыс. руб.);
для пути P7: 2 (дня) ´ 2 (тыс. руб./день) = 4 (тыс. руб.);
а всего 4 тыс. руб. + 4 тыс. руб. = 8 тыс. руб.
Следовательно, вариант сокращения работы В на 2 дня более эффективен, чем вариант сокращения А и Е на один день и F на два дня.
Для достижения заданного срока строительства в 57 дней необходимо сократить критическое время еще на два дня. Сделать это можно двумя способами. Первый - сократить работу С на 2 дня; второй - сократить А и Е на один день каждую и F сократить на два дня. В первом случае критическое время станет равным 57 дням, длительность полного пути P6 станет равной 56 дням, и путь P6 не превратится в критический. Во втором случае критическое время также станет 57 дней, но путь P6 превратится в критический, так как его продолжительность за счет сокращения работы А на один день станет равной 57 дням. Теперь сравним дополнительные затраты на ускорение работ по этим способам:
* для первого 2 (дня) ´ 4 (тыс. руб./день) = 8 (тыс. руб.);
* для второго 1 (день) ´ 2 (тыс. руб./день) + 1 (день) ´ 2 (тыс. руб./день) + 2 (дня) ´ 2 тыс. руб./день) = 8 (тыс. руб.).
Следовательно, по размеру дополнительных затрат эти способы эквивалентны, и можно выбирать любой из них. Более предпочтительным можно считать первый, поскольку по этому варианту сокращению подлежит одна работа С, а не три (А, Е, F), и количество критических путей не увеличивается. Итак, сокращаем продолжительность выполнения работы С на 2 дня, в результате чего получим:
критическое время Ткр = 57 дней,
критические пути Р5 = (С, А, Е, В), Р7 = (С, F, В),
общие дополнительные затраты 6 + 8 = 14 (тыс. руб.).
Сетевой график строительства торгового павильона в ускоренном режиме приведен на рис. 4.11.

Рис. 4.11. Сетевой график строительства павильона в ускоренном режиме
Итоговый ответ решения задачи 4 запишем в следующем виде
|
|
|
|


