 |
Классификация систем распознавания образов реального времени
|
|
|
|
В основе любой классификации лежат определенные классификационные признаки (принципы). Так, Горелик А.Л., Скрипкин В.А. в своей работе в качестве квалификационного признака используются свойства информации, которая применяется в процессе распознавания. Однако такая классификация не отражает всех характеристик системы реального времени (РВ), поэтому была разработана классификация по свойствам управления систем распознавания образов (СРО) в процессе распознавания (Рис. 1).
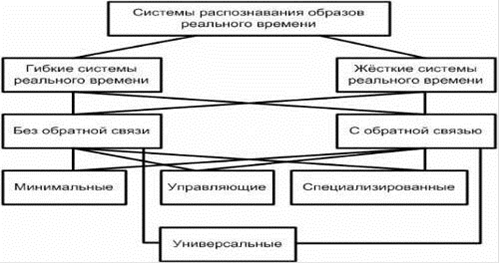
Рис. 1. Классификация СРО РВ
Принцип классификации по контролю времени распознавания образов разделяет СРО, на неконтролируемые по времени (т.е. не системы РВ и поэтому не отражены на рисунке 1), гибкие системы РВ и жёсткие системы РВ. Жёсткие СРО РВ характеризуются наличием жёстких сроков для каждого случая распознавания (в них обязательно необходимо укладываться). Гибкие СРО РВ отличаются тем, что нарушения сроков распознавания нежелательны, но допустимы. К неконтролируемым по времени системам относятся такие системы, которые проектируются для распознавания каких-либо объектов без конкретных сроков.
Если в качестве принципа классификации использовать влияние выходных результатов распознавания на управление системой, то СРО РВ можно разделить на системы без обратной связи и с обратной связью. Системы без обратной связи в самом простейшем случае можно описать в виде: Y = f (X) (Рис. 2).

Рис. 2. СРО РВ без обратной связи
Блок распознавания принимает на вход данные в некотором формате X от блока предварительной обработки данных (к примеру, этот блок отвечает за создание изображений для распознавания, поступающих с видеокамеры), и выдает результат Y, который блоком формирования результата тем или иным способом доносится до пользователя либо до системы принятия решения. Примером таких систем без обратной связи являются системы детектирования движений, системы распознавания штриховых кодов, системы распознавания автомобильных номеров, системы неразрушающего контроля, основанные на распознавании некоторых, характеризующих объект признаков.
|
|
|
Системы с обратной связью используют данные о предыдущих результатах распознавания с целью настройки системы под конкретные образы и условия распознавания. Работа таких систем может описываться выражениями
= f (Xt, Yt-1), Xt = f (Xt, Yt-1)
где t - текущий момент распознавания.
В данных системах результаты распознавания могут влиять не только на параметры работы функции распознавания, но и на предварительную обработку и формирование данных (Рис. 3).
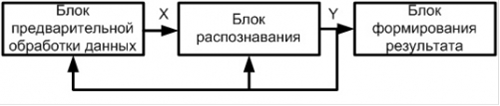
Рис. 3. СРО РВ с обратной связью
Примером систем с обратной связью являются системы оптического трекинга объектов, где предыдущее расположение объектов влияет на определение текущего местоположения, системы распознавания в подвижных роботах. Кроме того, многие системы без обратной связи могут быть модернизированы за счёт обработки результата распознавания (например, адаптивная система распознавания штриховых кодов).
Принцип классификации по автономности разделяет СРО РВ в соответствии со стандартом POSIX.13-2003:
• минимальные системы РВ;
• управляющие системы РВ;
• специализированные системы РВ;
• универсальные системы РВ.
Отличия данных систем обусловлены усложнением с программной точки зрения и поддержки аппаратных средств. Так минимальные системы РВ должны работать в составе АСУ, а универсальные системы являются самодостаточными.
2.4 Значение и некоторые задачи математической теории распознавания образов
Математическая теория распознавания образов возникла, должно быть, одновременно с теорией искусственного интеллекта, являясь одним из ее разделов. Специалисты по распознаванию образов пытаются построить алгоритмы, повторяющие элементы человеческого мышления (прежде всего абстрактного) и предшествующего ему обучения на конкретных примерах. По-видимому, одна из первых задач распознавания образов была сформулирована в работах биолога Ф.Розенблатта, посвященных имитации зрительного анализатора. Потребовалось построить алгоритм распознавания простейших изображений - например, цифр или букв. И до сих пор задачи такого рода остаются в распознавании образов наиболее популярными.
|
|
|
Другими задачами, в которых эффективными оказываются подходы распознавания образов, являются задачи анализа больших массивов эмпирических данных. К примеру, математическая теория распознания используется в медицине - в частности, с математическим обеспечением дифференциальной диагностики.
В этом случае в качестве объектов для распознавания выступают таблицы, содержащие огромное количество цифр - результатов различных медицинских исследований. Так, общий анализ крови человека включает порядка пятидесяти разных показателей, изучив которые, врач должен принять какое-то решение. Хороший врач, как правило, принимает это решение, опираясь на свой профессиональный опыт. Поэтому задача была - построить такой алгоритм принятия решения, чтобы, основываясь на прежнем опыте (базах данных по реальным историям болезни), опознавать новые случаи, помогая практикующему врачу с постановкой диагноза.
Более интересны математические задачи, связанные с дискретной оптимизацией, с теорией сложности алгоритмов, статистическими задачами принятия решений. Допустим, для обучения предоставлен некий материал. В случае медицинской диагностики это может быть обширная база данных по обследованию больных и здоровых людей. Задача состоит в том, чтобы на ее основе построить алгоритм, некое решающее правило, которое можно впоследствии использовать для диагностики. Причем главной проблемой является экстраполяционная (обобщающая) способность этого правила: с какой вероятностью оно будет правильно классифицировать нового пациента, данные о котором не использовались при обучении? По мере развития теории распознавания образов появляются все более совершенные алгоритмы и математические утверждения, позволяющие прогнозировать, что при каких-то условиях заданный алгоритм будет выдавать именно те значения, которые мы ожидаем. Как раз в этом направлении и удается получать довольно любопытные результаты. Здесь следует упомянуть заслуги советских математиков В.Н. Вапника, А.Я. Червоненкиса, Ю.И.Журавлева и др. Свердловская школа распознавания образов, родоначальником которой является профессор Вл.Д.Мазуров, является одной из ведущих в России. Разработанная здесь теория комитетных алгоритмов распознавания опирается на результаты Сергея Николаевича Черникова и Ивана Ивановича Еремина по теории линейных неравенств и математического программирования.
|
|
|
Проблема распознавания в течение достаточно продолжительного времени привлекает внимание специалистов в области прикладной математики, а затем и информатики. Центральная задача распознавания образов - построение на основе систематических теоретических и экспериментальных исследований эффективных вычислительных средств для отнесения формализованных описаний ситуаций и объектов к соответствующим классам. В основе такого отнесения лежит получение некоторой агрегированной оценки ситуации, исходя из ее описания. При условии установления соответствия между классами эквивалентности, заданными на множестве объектов распознавания, автоматизация процедур распознавания становится элементом автоматизации процессов принятия решений.
Становление распознавания служит отличной моделью развития математической теории обработки и преобразования информации, развития, в процессе которого эвристические методы получают строгое обоснование и начинают применяться в рамках вполне формализованных регулярных процедур.
Само распознавание является достаточно разработанным вариантом такой теории, поскольку позволяет разрешать ее основную задачу - синтезировать и выбирать алгоритмические средства для извлечения полезной информации из данных.
|
|
|
К постановке задачи распознавания прибегают в тех случаях, когда трудно строить формальные теории и применять математические методы, что происходит обычно по двум причинам:
а) уровень формализации соответствующей предметной области или доступная информация таковы, что не могут составить основу для синтеза математической модели, отвечающей классическим математическим или математико-физическим канонам и допускающей изучение классическими аналитическими или численными методами;
б) математическая модель в принципе может быть построена, однако ее синтез или изучение связаны с такими затратами, что они существенно превышают выигрыш, приносимый искомым решением, либо выходят за пределы существующих технических возможностей, либо делают решение задачи просто бессмысленным. «Двойственность» распознавания проявилась в том, что решение таких задач ввело в обиход большое число эвристических алгоритмов. Довольно долго подавляющее большинство приложений теории распознавания было связано с плохо формализованными областями - медициной, геологией, социологией, химией и т.д. В этих областях еще трудно строить формальные теории и применять стандартные математические методы. В лучшем случае удается дать математическое оформление некоторым интуитивным принципам и затем применять полученные «эмпирические формализмы» для решения частных задач. При исследовании задачи или класса задач на базе так называемых «правдоподобных» рассуждений предлагался нестрогий, но содержательно разумный метод решения и основанный на нем алгоритм; обоснование же производилось непосредственно в эксперименте с задачами. Алгоритмы, выдержавшие подобную экспериментальную проверку, т.е. приносившие успех при решении определенных практических задач, применяются, несмотря на отсутствие математических обоснований. Второй этап развития теории распознавания отличался попытками ставить и решать задачу выбора в конкретной ситуации наилучшего в некотором смысле алгоритма и попытками переходить от описания отдельных некорректных алгоритмов к описанию принципов их формирования, т.е. попытками строить единообразные описания для множеств эвристических, но успешно решающих реальные задачи.
Потребность в синтезе моделей алгоритмов распознавания в первую очередь определялось необходимостью фиксировать каким-то образом класс алгоритмов при выборе оптимальной или хотя бы приемлемой процедуры решения конкретной задачи. В свою очередь, попытки построения таких моделей породили интерес к собственно «математическим» свойствам алгоритмов распознавания, в особенности их строгого обоснования. Оказалось, что получение описания класса алгоритмов распознавания представляют собой задачу, сходную с построением классического определения алгоритма.
|
|
|
Изучение моделей распознающих алгоритмов позволило получать интересные теоретические результаты и решать разнообразные прикладные задачи. Вместе с тем данному методу решения задач распознавания присущи и некоторые серьезные недостатки, которые не могут быть устранены при рассмотрении лишь отдельных моделей. Для преодоления этих трудностей была предложена общая теория распознающих алгоритмов, построенная на основе алгебраического подхода к решению задач распознавания, обеспечивающего эффективное исследование и конструктивное описание класса алгоритмов распознавания и предусматривающего введение такого определения алгоритма распознавания, в рамки которого укладываются все существующие модели алгоритмов.
Алгебраический подход предусматривает обогащение исходных эвристических семейств алгоритмов при помощи алгебраических операций и построение семейства, гарантирующего получение корректного алгоритма, обеспечивающего решение изучаемого класса задач. В его основе лежит идея индуктивного порождения математических объектов посредством обобщенного индуктивного определения. Выделяются базисные алгоритмы и модели распознавания и вводятся операции над ними, позволяющие последовательно порождать новые алгоритмы и модели. Выясняются условия, при которых данное семейство алгоритмов является базисным относительно выведенных операций, а также свойства, которыми должна обладать модель для того, чтобы в ней нашелся алгоритм, правильно классифицирующий все объекты произвольной конечной выборки. Формируются методы построения таких алгоритмов.
В алгебраическом подходе существенно используются особенности структуры, свойственные любой процедуре распознавания. Он предусматривает введение так называемого пространства оценок, промежуточного по отношению к исходным описаниям и допустимым ответам.
Алгоритм распознавания при этом рассматривается как суперпозиция двух операторов. Первый из этих операторов - распознающий - в качестве ответов формирует элементы, называемые оценками, а второй - по оценкам определяет окончательные ответы.
Методология распознавания используется в информатике в двух качествах:
· во-первых, по прямому назначению для решения задач распознавания в классическом смысле;
· во-вторых, как средство точного исследования плохо определенных задач.
В последнем случае эта методология реализовывается приблизительно следующим образом. Пусть, например, имеются некоторые данные, полученные в результате физического или имитационного эксперимента. Эти данные в некотором весьма ограниченном смысле характеризуют изучаемые объект или явление; необходимо их воедино с тем, чтобы установить, какие закономерности отражаются в имеющемся материале. Для этого выдвигается некоторая простая гипотеза, которой придается математический облик, и делается попытка «объяснить» имеющийся материал с ее помощью. Последовательное использование ряда эвристик может позволить угадать модель. В противном случае происходит переход к поиску оптимального эвристического принципа - модели. Если оказывается, что соответствующего принципа не существует или им нельзя практически воспользоваться, то следует формировать некоторый конгломерат принципов, обеспечивающий выделение «федеративного» принципа; именно этот верхний уровень и соответствует возможностям и назначению алгебраического подхода.
Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости. Однако, на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, изменяются значения параметров на выходе системы. Результаты измерения заносятся в таблицу. В результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию. Задача, возникающая перед исследователем, состоит в отыскании соответствующего аналитического выражения для функции, т.е. распознать табличную функцию. Для этой цели могут быть употреблены тригонометрические ряды, поскольку есть уверенность, что эта функция приближенно и достаточно точно может быть выражена суммой конечного числа первых членов ее ряда Фурье. Весь вопрос заключается в нахождении коэффициентов Фурье функции.
Пусть в интервале  задана функция
задана функция 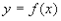 . Мы считаем, что при любом задании функции график ее нам известен. При этом в случае необходимости систему координат Оху следует параллельным сдвигом перенести так, чтобы весь график был расположен над осью Ох и как можно ближе к ней (рис. 1). Это скажется только на свободном члене разложении Фурье, а вместе с тем позволит избежать как отрицательных, так и слишком больших положительных значений функции.
. Мы считаем, что при любом задании функции график ее нам известен. При этом в случае необходимости систему координат Оху следует параллельным сдвигом перенести так, чтобы весь график был расположен над осью Ох и как можно ближе к ней (рис. 1). Это скажется только на свободном члене разложении Фурье, а вместе с тем позволит избежать как отрицательных, так и слишком больших положительных значений функции.
Приближенное представление функции в виде многочлена Фурье требует отыскания первых коэффициентов Фурье


Рис. 1.
Приведем алгоритм решения задачи.
. Задается функция 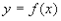 в интервале
в интервале  .
.
. Интервал  делится на п равных частей с помощью точек
делится на п равных частей с помощью точек
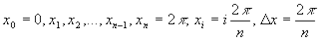 .
.
. Вводятся значения входных параметров (xi, yi)
. Вычисляются коэффициенты ak,,bk

где 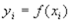 .
.
5. Получаем приближенное выражение функции в виде тригонометрического многочлена
 .
.
Принимая во внимание особенности множителей coskxi и sinkxi, берут п чаще всего равным 12 или 24. Мы здесь возьмем п=12.
| xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| yi | 44 | 46 | 76 | 88 | 86 | 63 | 24 | 20 | 26 | 40 | 58 | 65 |
Вычисляем коэффициенты ak,,bk..
Так как соs0=1
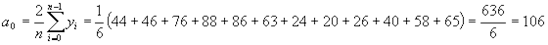 ,
,
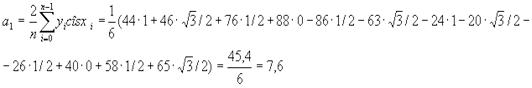

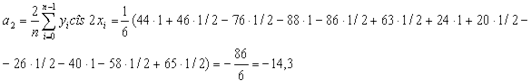
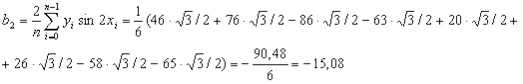
Таким образом, получаем приближенное выражение функции в виде тригонометрического многочлена второго порядка

Думаю, что на современном этапе развития вычислительной техники задача создания искусственного интеллекта пока неразрешима. Однако в частных случаях компьютерный мозг может работать ничуть не хуже человеческого. Например, американская почтовая служба объявила конкурс на создание наиболее точно работающего алгоритма по распознаванию рукописных цифр для автоматизации обработки корреспонденции. Для чистоты эксперимента эмпирические массивы, предназначенные для обучения и тестирования алгоритмов, были фиксированы заранее. В результате были созданы алгоритмы, обеспечившие меньший процент ошибок на контроле, чем человек-эксперт.
Что же касается будущего идеи искусственного интеллекта… Уже сегодня много говорится о так называемых квантовых вычислениях и квантовых компьютерах. Возможно, когда квантовые машины станут реальностью, мы и подойдем к решению этой задачи.
ЗАКЛЮЧЕНИЕ
Распознавание образов (а часто говорят - объектов, сигналов, ситуаций, явлений или процессов) - самая распространенная задача, которую человеку приходится решать практически ежесекундно от первого до последнего дня своего существования. Для этого он использует огромные ресурсы своего мозга, которые мы оцениваем таким показателем как число нейронов, равное 1010.
Можно заметить, что похожие действия наблюдаются в биологии, в живой природе, а иногда даже в неживой. Кроме того, распознавание постоянно встречается в технике. А если это так, то, очевидно, следует считать механизм распознавания всеобъемлющим.
В повседневной деятельности человек постоянно сталкивается с задачами, связанными с принятием решений, обусловленных непрерывно меняющейся окружающей обстановкой. В этом процессе принимают участие: органы чувств, с помощью которых человек воспринимает информацию извне; центральная нервная система, осуществляющая отбор, переработку информации и принятие решений; двигательные органы, реализующие принятое решение. Но в основе решений этих задач лежит, в чем легко убедиться, распознавание образов.
В своей практике люди решают разнообразные задачи по классификации и распознаванию объектов, явлений и ситуаций (мгновенно узнают друг друга, с большой скоростью читают печатные и рукописные тексты, безошибочно водят автомобили в сложном потоке уличного движения, осуществляют отбраковку деталей на конвейере, разгадывают коды, древнюю египетскую клинопись и т.д.).
Вычисления в сетях формальных нейронов, во многом напоминают обработку информации мозгом. В последнее десятилетие нейрокомпьютинг приобрел чрезвычайную популярность на Западе, где он уже успел превратиться в инженерную дисциплину, тесно связанную с производством коммерческих продуктов. Ежегодно выходят десятки книг, посвященных практическим аспектам нейрокомпьютинга. Интенсивно ведутся работы по созданию новой - аналоговой элементной базы для нейровычислений.
В России же, где в силу общего снижения тонуса научных исследований структура науки оказалась «замороженной», до сих пор бытует мнение, что традиционные математические методы в принципе достаточны для решения любых задач распознавания образов. Нейрокомпьютинг же воспринимается как излишество и дань кратковременной моде. Однако на фоне многочисленных практических успехов нейротехнологии утверждения, что любая конкретная задача может быть в принципе решена и без них выглядят несколько схоластично. Раз нейрокомпьютинг на деле доказывает свою конкурентоспособность разумнее повнимательнее приглядеться к этому феномену.
Перспективы в ближайшем будущем. Основной чертой, отличающей нейрокомпьютеры от современных компьютеров и обеспечивающей будущее этого направления, является способность решать неформализованные проблемы, для которых в силу тех или иных причин еще не существует алгоритмов решения. Нейрокомпьютеры предлагают относительно простую технологию порождения алгоритмов путем обучения. В этом их основное преимущество, их «миссия» в компьютерном мире.
Возможность порождать алгоритмы оказывается особенно полезной для задач распознавания образов, в которых зачастую не удается выделить значимые признаки априори. Вот почему нейрокомпьютинг оказался актуален именно сейчас, в период расцвета мультимедиа, когда развитие глобальной сети Internet требует разработки новых технологий, тесно связанных с распознаванием образов.
Список использованной литературы
1. Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Метод потенциальных функций в теории обучения машин. - М.: Наука, 2004. - 384 с.
2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. - М.: Наука, 1971г.
. Бородаенко Д.Н. Распознавание образов // Распознавание образов и искусственный интеллект. 2001. http://www.ocrai.narod.ru (26.12.2007).
4. Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов. - СПб.: Питер, 2003. 688 с.
. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М,: Наука, 1974.
6. Воронцов К. В. Лекции по статистическим (байесовским) алгоритмам классификации, 2008.
. Горелик А.Л., Гуревич И.Б., Скрипкин В.А. Современное состояние проблемы распознавания. Издательство: Радио и связь. 1985, 160 с.
8. Горелик А.Л., Скрипкин В.А. Методы распознавания. М.: Высш. шк, 2004. 261 с.
. Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации// Проблемы кибернетики. М.: Наука, 2005. Вып. 33. С. 5-68
. Журавлев Ю.И. Избранные научные труды. Изд. Магистр, 2002. - 420 с.
. Каримов Р.Н. Обработка экспериментальной информации. Уч. Пособие. Ч. 3. Многомерный анализ. СГТУ, Саратов, 2000, 108 с.
. Ким Дж, Мьюллер Ч.У. и др. Факторный, дискриминантный и кластерный анализ. Пер. с англ. М.: Финансы и статистика, 1989, 215 с.
. Лепский А.Е., Броневич А.Г. Математические методы распознавания образов: Курс лекций.- 2009.
. Лиховидов В.Н. Практический курс распознавания образов. - Владивосток: издательство ДВГУ, 1983.
. Мазуров Вл.Д. Математические методы распознавания образов. Учебное пособие. 2010 г., 101 с.
. Мазуров В.Д. Комитеты систем неравенств и задача распознавания // Кибернетика, 2004, № 2. С. 140-146.
. Математические методы распознавания образов // Доклады 11-й Всероссийской конференции. - 2003. - 18 апр. - С.18.
. Н.С.Пискунов „Дифференциальное и интегральное исчисления”, Москва, „Наука”, 1972 г.
. Потапов А.С. Распознавание образов и машинное восприятие. - С-Пб.: Политехника, 2007. - 548 с
20. Распознавание, классификация прогноз. Математические методы и их применение. - М.: Наука, 1989 г.
21.Ту Дж., Гонсалес Р. Принципы распознавания образов. - М.: Мир, 1978, 411 с.
. Файн В. С. Опознавание изображений, М. 1970
. Фихтенгольц Г.М. Основы математического анализа. М.: Гостехиздат, 1956.
. Фихтенгольц Г.М. „Курс дифференциального и интегрального исчисления”, том III, Москва, „Наука”, 1969г.
. Ф. Розенблатт. Принципы нейродинамики. Перцептроны и теория механизмов мозга. Издательство: Мир.1965 г.
. Фу К. Структурные методы в распознавании образов. - М.: Мир, 2005. - 144 с.
. Фу. К. Последовательные методы в распознавании образов и обучении машин/ К. Фу. - М.: Наука, 1971. - 355 с.
. Фукунага К. Введение в статистическую теорию распознавания образов/ К. Фукунага - М.: Наука, 1979. - 267 с.
. Эдвард А. Патрик. Основы теории распознавания образов. Пер. с англ. Под ред. Б.Р.Левина. Издательство: М.: "Советское радио".1980. 864 с.
|
|
|


