 |
Компоновка усложненного типа балочной клетки
|
|
|
|

Рисунок 3 – Схема усложненного типа балочной клетки
Расстояние между балками настила и вспомогательными балками принимаем конструктивно из условия, что нагрузка считается равномерно распределенной, если она приложена не менее чем в 5 точках. Вспомогательных балок берем 6, а балок настила можно брать 5 или 6.
Пример расчета:
БН:  мм
мм
ВБ:  мм
мм
Определим нормативную и расчетную нагрузку на балку настила
| Gн=1,02(pн+qн)a | (6) |
где: pн - нагрузка на настил
qн – вес настила
a – шаг балок
Gн=1,02(16+0,942)1,083=18,72 кН/м2
Gp=1.02(γf1 pн +γf2 qн)a
γf1 - коэффициент перегрузки, принимаем равным 1,2
γf2 – коэффициент надежности по нагрузке, принимаем равным 1,05
Gp=1,02(1,2*16+1,05*0,942)1,083=22,3 кН/м
Статический расчет балки настила при усложненном типе балочной клетке
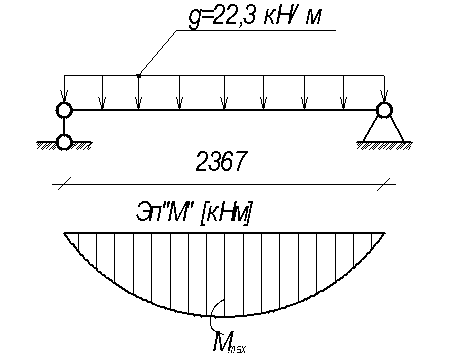
Рисунок 4 – Расчетная схема балки настила при усложненном типе балочной клетке
Найдем изгибающий момент в наиболее опасном сечении, т.е. в середине пролета балки.
Пример расчета:

| (7) |
где: q - расчетная нагрузки, т.е. Gp
l – данная длинна пролета балки, т.е. α
Найдем требуемый момент сопротивления

| (8) |
| (9) |
Учитывая условие, что Wтр<Wx по сортаменту на странице 543 [1] подбираем двутавр №12
Данные двутавра:
Момент сопротивления Wx=58,4 см3
Толщина стенки tw=4,8 мм
Линейная плотность ρx=11,5 кг/м
Высота балки h=120 мм
Ширина полки bf=64 мм
Средняя толщина полки tf=7,3 мм
Момент инерции Ix=350 см4
Найдем фактический коэффициент C1 по таблице 60 [2]

Применяя метод интерполяции по полученному отношению Af/At=0.81, вычислим коэффициент C1
C1=1,04
Найдем процент недонапряжения
 кН/см3
кН/см3
Должно выполняться условие 
Ry γc=31,5*1=31,5

Проверка жесткости балки настила

| (10) |
где: gн – погонная нагрузка
|
|
|
l – данная длинна пролета балки
Ix – момент инерции
Е – модуль упругости стали
 - прогиб
- прогиб
 - допустимый прогиб
- допустимый прогиб
Пример расчета:

Статический расчет вспомогательной балки при усложненном типе
Балочной клетки
Определим нормативную и расчетную нагрузку на вспомогательную балку:
| Gн=1,02(pн+qн)a | (11) |
где: pн - нагрузка на настил
qн – вес настила
a – шаг балок
Пример расчета:

Рисунок 5 – Расчетная схема вспомогательной балки при усложненном типе
балочной клетке
Gн=1,02(16+0,942)2,366=40,89 кН/м2
Gp=1.02(γf1 pн +γf2 qн)a
γf1 - коэффициент перегрузки, принимаем равным 1,2
γf2 – коэффициент надежности по нагрузке, принимаем равным 1,05
Gp=1,02(1,2*16+1,05*0,942)2,366=48,72 кН/м
Найдем изгибающий момент в наиболее опасном сечении, т.е. в середине пролета балки.

где: q - расчетная нагрузки, т.е. Gp
l – данная длинна пролета балки
Найдем требуемый момент сопротивления

Учитывая условие, что Wтр<Wx по сортаменту на странице 543 [1] подбираем двутавр №36
Данные двутавра:
Момент сопротивления Wx=743 см3
Толщина стенки tw=7,5 мм
Линейная плотность ρx=48,6 кг/м
Высота балки h=360 мм
Ширина полки bf=145 мм
Средняя толщина полки tf=12,3 мм
Момент инерции Ix=13380 см4
Найдем фактический коэффициент C1 по таблице 60 СНиП II-23-81* «Стальные конструкции»

Применяя метод интерполяции по полученному отношению Af/At=0,66, вычислим коэффициент C1
C1=1,101
Найдем процент недонапряжения:
 кН/см3
кН/см3
Должно выполняться условие 
Ry γc=31,5*1=31,5


| (12) |
где: gн – погонная нагрузка
l – данная длинна пролета балки
Ix – момент инерции
Е – модуль упругости стали
 - прогиб
- прогиб
 - допустимый прогиб
- допустимый прогиб

3 Экономическое сравнение вариантов
Выбор наиболее рационального варианта типа балочной клетки осуществляем по результатам расчётов, помещённых в таблице 1. При расчёте показателей таблицы 1 можно пользоваться приближенными формулами расчёта.
|
|
|
Таблица 1 – Экономическое сравнение вариантов
| Расчетные формулы и величины | Результаты расчета | ||
| вариант 1 | вариант 2 | ||
| балка настила | вспомога- тельная балка | ||
| 1. Толщина настила, см | 1,2 | 1,2 | |
| 2. Вес настила кН/м2 | 0,942 | 0,942 | |
| 3. Расчетная нагрузка кН/м | 36,55 | 22,3 | 48,72 |
4.  кНм кНм
| 193,03 | 15,6 | 257,3 |
5. 
| 557,09 | 45,02 | 742,57 |
| 6. Сечение: № I; Wx, см3; Ix, см4; ρ, кг/м | №33; 597; 9840; 42,2 | №12; 58,4; 350; 11,5 | №36; 743; 13380; 48,6 |
7. 
| 3,52≤3,25 | 1,048≤1,57 | 3,45≤4,33 |
| 8. Расход стали кг/м3 | 
| 
|
Анализ данных таблицы 1 показывает, что минимальными затратами материалов и стоимостью обладает первый вариант балочной клетки, который в дальнейшем принимаем за разрабатываемый.
Вывод: наиболее выгодный первый вариант, так как при этом варианте, расходуется, меньше стали. Принимаем первый вариант за основной.
|
|
|


