 |
Проверка наличия положительного эффекта от НЧ фильтрации речевого сигнала, маскируемого белым шумом, путем моделирования в среде Matlab
|
|
|
|
Цифровая фильтрация речевых сигналов
Цели работы:
1) освоение приемов фильтрации речевых сигналов;
2) освоение способов синтеза цифровых винеровских фильтров
Рабочее задание
1. Рассчитать выигрыш в отношении сигнал-шум, достигаемый при использовании НЧ фильтрации речевого сигнала, маскируемого белым шумом.
2. Экспериментально оценить эффективность НЧ фильтрации речевого сигнала, маскируемого белым шумом, с помощью моделирования в среде Matlab-SPTool.
3. Экспериментально оценить эффективность винеровской вильтрации:
3.1. Синтезировать оптимальный цифровой винеровский КИХ фильтр методом обратного преобразования Фурье. Произвести цифровую фильтрацию смеси речевого сигнала с шумом. Сравнить сигналы до и после фильтрации.
3.2. Синтезировать оптимальный цифровой винеровский КИХ фильтр путем численного решения интегрального уравнения Фредгольма 1-го рода. Произвести цифровую фильтрацию смеси речевого сигнала с шумом. Сравнить сигналы до и после фильтрации.
Требования к оформлению отчета:
1. Графики сигналов и их спектров до и после фильтрации, а также АЧХ и ИХ использовавшихся фильтров.
2. Комментарии к графикам
3. Листинги вычислительных программ
4. Выводы по работе
Контрольные вопросы:
1. Объясните причины невысокой эффективности НЧ фильтрации смеси речевого сигнала с помехой.
2. Почему винеровская фильтрация называется оптимальной?
3. Какие способы синтеза винеровского фильтра вам известны?
4. Объясните технологию синтеза винеровского фильтра на «частотном языке».
5. Объясните технологию синтеза винеровского фильтра на «временном языке».
6. Как осуществить фильтрацию сигнала после того, как фильтр синтезирован?
|
|
|
Теоретические сведения
Приближенная оценка выигрыша в отношении сигнал-шум за счет НЧ фильтрации
Спектр речевого сигнала сосредоточен в области частот 100-3500 Гц – его приближенно можно считать существующим в области частот 0-3500 Гц. Спектр белого шума воспринимается ухом человека в области частот 20-20000 Гц, его приближенно можно считать существующим в области частот 0-20000 Гц.
Если осуществить фильтрацию аддитивной смеси речевого сигнала и шума с помощью НЧ фильтра, частота среза которого 
Гц, тогда мощность помехи понизится в 20000/3500 = 5,7 раза (рис.1) или в 10log5,7=7,6 дБ.
Рис.1. НЧ фильтрация речевого сигнала
Проверка наличия положительного эффекта от НЧ фильтрации речевого сигнала, маскируемого белым шумом, путем моделирования в среде Matlab
Запишем речевой сигнал в виде wav-файла с параметрами: частота дискретизации 
Гц, моно, 16 бит. Для записи можно использовать телефонную гарнитуру и программу «Звукозапись» из группы «Стандартные|Развлечения». В качестве альтернативной программы записи можно также использовать команду wavrecord среды Matlab.
Если звуковой файл записывался с помощью программы «Звукозапись», его следует импортировать в среду Matlab:
rech2=wavread(‘rech2.wav’);
Примечание 1. Если звуковой файл записывался средствами Matlab, в таком импортировании нет необходимости, поскольку файл создается в виде одномерного массива в рабочем пространстве Matlab:
rech2=wavrecord(220500,44100,'double');
(здесь n=220500 – количество отсчетов записываемого сигнала, соответствующее длительности сигнала 5 с при частоте дискретизации Fs=44100 Гц; ‘double’ – опция, указывающая на запись в формате 16 бит/отсчет).
Примечание 2. Если звуковой файл записывался средствами Matlab, тогда для сохранения его на винчестере следует использовать команду wavwrite (синтаксис этой команды смотрите в разделе Help программы Matlab).
Располагая массивом rech2, далее проделаем следующие действия:
|
|
|
· оценим стандартное отклонение речевого сигнала (среднее на интервале существования сигнала);
· сгенерируем отрезок дискретного белого гауссовского шума с утроенным стандартным отклонением;
· сложим речевой сигнал с помехой, в результате отношение сигнал-шум для полученной смеси будет равно 1/9 (или, что то же, -9,5 дБ, т.е. почти -10 дБ).
Команды Matlab для реализации таких действий:
std_rech=std(rech2); % измерение станд.откл. речевого сигнала
std_noise=3*std_rech; % станд.откл. шума
n=std_noise*randn(length(rech2),1); % генерирование шума
rech2_noise = rech2+n; % аддитивн.смесь
Прослушаем полученную смесь:
wavplay(rech2_noise,44100);
НЧ фильтрацию этой смеси удобно реализовать с помощью программы sptool, которая вызывается из командного окна командой:
Sptool
В результате активизации программы sptool на мониторе появляется окно ее графического интерфейса (рис.П.2).
Как следует из надписей на этом окне, данная программа позволяет работать с сигналами, их спектрами, синтезировать цифровые фильтры и пропускать сигналы через синтезированные цифровые фильтры. Как фильтруемые, так и фильтрованные сигналы могут быть визуализированы в виде графиков, а также прослушаны через наушники или мультимедийную аудиосистему компьютера.
Для того, чтобы такая обработка сигналов стала возможной, сигналы следует импортировать в среду программы sptool. Графики импортированных в среду sptool сигналов rech2 и rech2_noise приведены на рис.П.3 и П.4, соответственно.
График АЧХ синтезированного НЧ фильтра (КИХ фильтр с окном Кайзера, 
=3, порядок фильтра 34) показан на рис.П.5.
Рис.2. Окно графического интерфейса программы sptool
Сигнал rech2_denoise, представляющий собой результат НЧ фильтрации сигнала rech2_noise, показан на рис.5 – на графике достаточно хорошо видно возрастание уровня сигнала, обусловленное НЧ фильтрацией.
Рис.3. График сигнала rech2
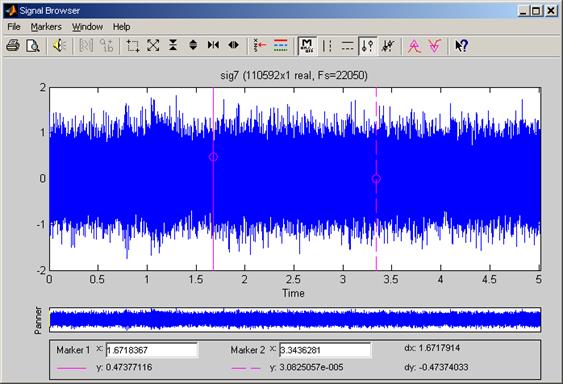
Рис.4. График сигнала rech2_noise
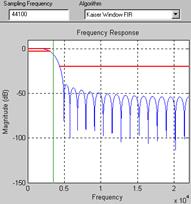
Рис.5. График синтезированного НЧ фильтра
Рис.6. График сигнала rech2_denoise
Улучшение разборчивости речи практически не ощущается.
Столь, казалось бы, странные результаты данного опыта объясняются основными положениями теории измерения разборчивости речи [3], согласно которым разборчивость речи определяется разборчивостью формант – спектральных составляющих элементарных «кирпичиков» речевого сигнала в виде фонем. Спектр формант сосредоточен главным образом в диапазоне частот 200-4000 Гц. Маскирующее действие на речевой сигнал оказывают близлежащие (в пределах критической полосы) спектральные компоненты шума. Поэтому, осуществляя НЧ фильтрацию с частотой среза 3500 Гц, мы лишь незначительным образом уменьшаем маскирующее действие шума. Как следствие – разборчивость речи практически не изменяется.
|
|
|
Отсюда следует важный вывод: для существенного повышения разборчивости речи необходимо подавлять помеху, сосредоточенную в той же полосе частот, что и речевой сигнал, т.е. в полосе частот 100-3500 Гц.
2. Синтез оптимального цифрового Винеровского КИХ фильтра методом обратного преобразования Фурье
При расчете низкочастотных КИХ-фильтров с линейной ФЧХ порядка 
методом обратного преобразования Фурье коэффициенты 
, вычисляют [1] по формуле:
, (21)
где 
, 
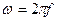, - ЧХ идеального цифрового НЧ-фильтра, обычно задаваемая в виде прямоугольника (рис.П.7) единичной высоты и шириной 
; 
- граничная частота полосы пропускания. 
- период дискретизации;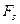 
- частота дискретизации.
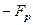0 
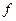
Рис.П.7
Алгоритм фильтрации при этом имеет вид:
, (22)
где 
и 
- отсчеты входного и выходного сигналов в момент времени 
; 
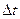- период дискретизации.
Выражение для частотной характеристики винеровского фильтра:
.
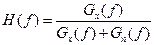Синтез винеровского фильтра в среде Matlab осуществим с помощью функции fir2, позволяющей синтезировать цифровые КИХ фильтры с АЧХ значительно более сложной формы. При этом, в сущности, требуемая АЧХ задается массивами значений частоты и соответствующих значений АЧХ.
Для измерения спектров смеси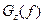 
и помехи 
используем оценку Уэлча (Welch) с параметрами: длина сегментов и длина весового окна Хэннинга Nfft=Nwin=1024; сегменты перекрываются на 512 отсчетов. Таким образом, разрешающая способность спектрального анализа равна 44100/1024=43 Гц (что близко к минимальной ширине критической полосы слуха).
Программа вычислений спектров смеси 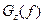и помехи :
|
|
|
Fs=44100; nfft = 1024; window = hanning(nfft); noverlap = 512; % окно Хана, перекрытие 50%
[Gz,fz] = pwelch(rech2_noise,window,noverlap,nfft,Fs); % оценка спектра смеси
plot(fz(1:128),Gz(1:128));
title('Спектр мощности смеси, Gz');
xlabel('Частота, Гц');ylabel('Уровень');
Figure
[Gn,fn] = pwelch(n,window,noverlap,nfft,Fs); % оценка спектра помехи
plot(fn(1:128),Gn(1:128));
title('Спектр мощности помехи, Gn');
xlabel('Частота, Гц');ylabel('Уровень');
Примерный вид графиков оценок спектров смеси 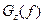и помехи показан на рис.П.8-П.9.
Рис.8. Оценка спектра 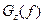Рис.9. Оценка спектра
Оценка требуемой АЧХ винеровского фильтра :
Figure; H=abs(1-Gn./Gz);
plot(fz(1:128),H(1:128));
title('Оценка АЧХ винеровского фильтра, H');
xlabel('Частота, Гц');ylabel('Уровень');
График оценки функции показан на рис.П.10.
Синтез винеровского фильтра 34-го порядка осуществим с помощью функции fir2:
f=fz/22050; m=H;
a=fir2(34,f,m); % 34 – порядок фильтра
[h,w]=freqz(a,1); % АЧХ синтезированного фильтра
figure; plot(w(1:180)*22050/pi,abs(h(1:180)));
title('АЧХ синтезированного винеровского фильтра, H');
xlabel('Частота, Гц');ylabel('Уровень');
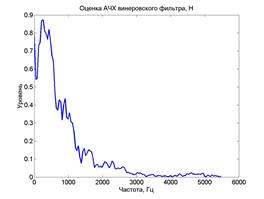
Рис. 10. Оценка Рис.11. Синтезированная АЧХ (34 порядок)
График АЧХ синтезированного винеровского КИХ фильтра 34 порядка показан на рис.П.11. Сравнивая рис.П.10 и П.11, видим, что вряд ли можно говорить о хорошем совпадении формы требуемой и синтезированной АЧХ. Увеличивая порядок фильтра до 250, получаем АЧХ, значительно лучше совпадающую с требуемой АЧХ (рис.П.12).
Рис. 12. Синтезированная АЧХ (250 порядок)
Произведем теперь цифровую фильтрацию смеси сигнала с шумом, используя коэффициенты синтезированного винеровского КИХ фильтра 250-го порядка.
rech2_denoise_10dB_wien250_spec=filter(a,1,rech2_noise);
График результата фильтрации представлен на рис.13. Сравнивая его с рис.6, нетрудно видеть заметно более высокое качество подавления помехи. Это не удивительно, поскольку эффективная полоса пропускания показанной на рис.П.12 АЧХ примерно вдвое меньше таковой для ситуации на рис..6.
Прослушивание речевого сигнала, фильтрованного синтезированным винеровским фильтром 250-го порядка, также свидетельствует о понижении уровня маскирующего шума, однако свидетельствует и о весьма существенном понижении разборчивости речи. При этом в первую очередь следует отметить плохое воспроизведение согласных звуков, вполне объяснимое тем, что спектры согласных звуков содержат высокочастотные компоненты.
Рис.13 Оценка спектра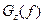
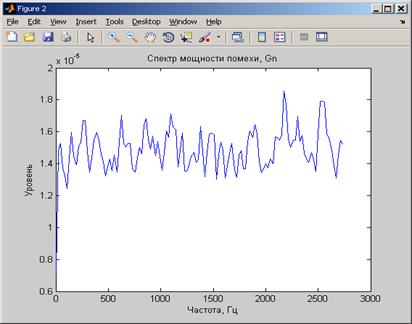
Рис13.– Оценка спектра
Рис14– Оценка
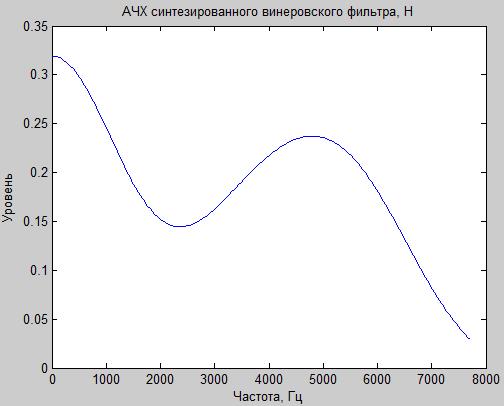
Рис15.– Синтезированная АЧХ (34 порядок)
Сравнивая рис.11 и рис.12, видим, что вряд ли можно говорить о хорошем совпадении формы требуемой и синтезированной АЧХ. Увеличивая порядок фильтра до 250, получаем АЧХ, значительно лучше совпадающую с требуемой АЧХ (рис.13).
Рис16.– Синтезированная АЧХ (250 порядок)
|
|
|
Вывод: в ходе выполнения данной лабораторной работы были освоены приемы фильтрации речевых сигналов, способы синтеза цифровых винеровских фильтров.
|
|
|
