 |
БПФ прореживанием по времени
|
|
|
|
Задачи работы
-написать программу на языке С реализующую один из алгоритмов быстрого преобразования Фурье.
Краткий конспект теоретической части
Основной алгоритм преобраования Фурье сложности О(N2)
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Перечислите виды алгоритмов БПФ
______________________________________________________________________________________________________________________________________________________________________________________________________ Опишите организацию цикла в языке С
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Опишите алгоритм БПФ прореживанием по времени и алгоритм прореживанием по частоте
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1. Теоретические сведения
Быстрое преобразование Фурье (БПФ, FFT) — это быстрый алгоритм вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем N 2, требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющего сложность O (N log(N))
|
|
|
Вывод преобразования из ДПФ
Дискретное преобразование Фурье для вектора 
, состоящего из N элементов, имеет вид:
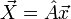
элементы матрицы 
имеют вид: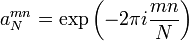 
.
Пусть N четно, тогда ДПФ можно переписать следующим образом:
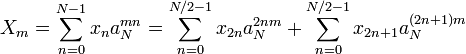
Коэффициенты 
и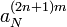 
можно переписать следующим образом (M=N/2):
В результате получаем:
То есть дискретное преобразование Фурье от вектора, состоящего из N отсчетов, свелось к линейной композиции двух ДПФ от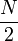 
отсчетов, и если для первоначальной задачи требовалось N 2операций, то для полученной композиции — 
.
Таким образом, можно продолжать разбиение исходной последовательности до тех пор, пока возможно деление последовательности на две. Очевидно, что если 
, 
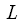– положительное целое, мы можем разделить последовательность пополам 
раз. Для 
(
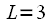) такое разбиение представлено на рисунке.
Граф алгоритма БПФ с прореживанием по времени. Двоично-инверсная перестановка
Представим в виде графа алгоритм БПФ с прореживанием по времени основанный на разбиении — объединении при (рисунок 1).
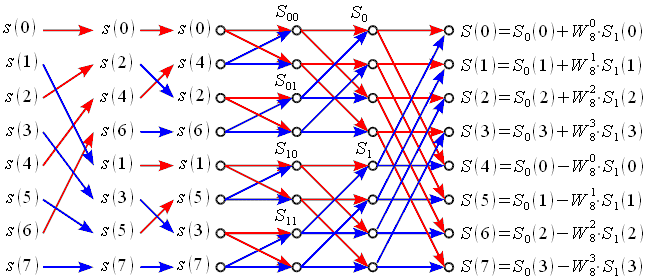
Рисунок 4: Граф алгоритма БПФ с прореживанием по времени при N=8
Разбиение и объединение последовательностей при N = 8
Так вот, если N является степенью двух, то это разделение можно продолжать рекурсивно до тех пор, пока не дойдем до двух точечного преобразования Фурье, которое вычисляется по следующим формулам:
Каждое разбиение делит последовательность на две половинной длительности (красную и синюю), а каждое объединение «собирает» из двух последовательностей одну удвоенной длительности.
Алгоритмы БПФ, которые используют выборки длиной , называются «алгоритмами БПФ по основанию 2». Данные алгоритмы получили наибольшее распространение, из-за того что в машинной арифметике является «круглым» числом.
Очевидно что делить последовательности на две можно по-разному, однако от этого зависит сможем ли мы при объединении получить неискаженный спектр сигнала и чего с точки зрения вычислительных затрат это будет нам стоить. Можно сказать, что эффективность алгоритма БПФ полностью зависит от способа разбиения и объединения последовательности, поскольку если не учитывать операции на разбиение-объединение, то для расчета спектра требуется 
раз посчитать ДПФ на 2 точки, в результате общее количество вычислительных операций составит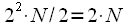 
, то есть количество операций линейно зависит от величины выборки.
|
|
|
Рассмотрим два способа разбиения — объединения: прореживание по времени и прореживание по частоте
БПФ прореживанием по времени
Для начала комплексную экспоненту в выражении (1) обозначим как:
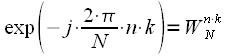
| (2) |
Тогда выражение (1) принимает вид:
| (3) |
Прореживание по времени заключается в разбиении исходной последовательности отсчетов 
, 
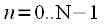на две последовательности длительност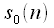и 
и 
, 
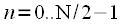, таких что 
, а 
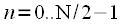, . Другими словами, последовательность 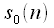содержит отсчеты последовательности с четными индексами, а - с нечетными. Прореживание по времени для N = 8 наглядно представлено на рисунке 2.
Рисунок 2: Прореживание по времени для N=8
|
|
|
