Вязкость газов в вакуумной технике

При перемещение твердого тела со скоростью  за счет передачи количества движения молекулам газа возникает сила внутреннего трения

В области низкого вакуума весь газ между подвижной 2 и неподвижной 1 пластинами (рис 1) можно разделить на слои толщиной  , где  – средняя длина свободного пути. Скорость движения каждого слоя различна и линейно зависит от расстояния между поверхностями переноса. В плоскости 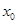 происходят столкновения молекул, вылетевших из плоскосте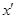й  и 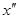 . Причиной возникновения силы вязкостного трения является, то что движущиеся как единое целое отдельные слои газа имеют разную скорость, вследствие чего происходит перенос количества движения из одного слоя в другой.

Изменение количества движения в результате оного столкновения равно 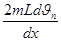 . Принимая, что в среднем в отрицательном и положительном направление оси  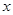в единицу времени единицу площади в плоскости  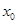пересекают  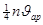молекул получим общее изменение количества движения в единицу времени для плоскости  :

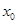 (1).

Сила трения по всей поверхности переноса, согласно второму закону Ньютона, определяется общим изменение количества движения в единицу времени:

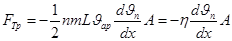 (2),

где 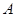 – площадь поверхности переноса;  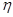– коэффициент динамической вязкости газа:

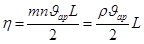 (3)

Отношение 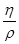 называют коэффициентом кинематической вязкости

Более строгий вывод, в котором учтен закон распределения скоростей и длин свободного пути молекул, дает

 ,

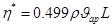что мало отличается от приближенного значения

Если в (3) подставить значения зависящих от давления переменных  , то

 . (7)

Согласно полученному выражению, коэффициент динамической вязкости при низком вакууме не зависит от давления.

Температурную зависимость коэффициента вязкости можно определить. если подставить в (3) 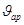 и  соответственно из формул:

 (6)

и

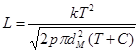
в формулу (3). Отсюда имеем:

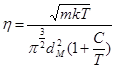 (4)

В соответствие с (4) 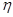 зависит от  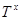, где 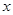 изменяется от ½ при высоких температурах  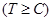до  при низких температурах при  . Во всех случаях коэффициент динамической вязкости увеличивается при повышение температуры газа.

Значения коэффициентов динамической вязкости для некоторых газов при  даны в таблице.

ТАБЛИЦА 1

 

Коэффициенты динамической вязкости
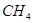
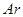
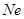
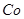
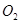
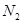
Газ										воздух
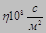
	0.88	1.90	1.10	2.10	3.00	1.75	1.70	2.02	1.40	1.70

Для двухкомпонентной смеси коэффициент динамической вязкости рассчитывается по формуле:

 ,

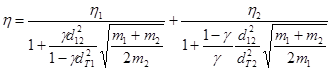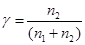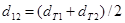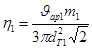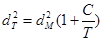где  ;  ;  ;  ;  и  находят из формулы  . Величина  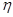в этом случае зависит от состава газовой смеси.

В области высокого вакуума молекулы газа перемещаются между движущейся поверхностью и неподвижной стенкой без соударения. В этом случае силу трения можно рассчитать по уравнению:

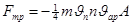 (5)

Знак «–» в формуле (5) означает, что направление силы трения противоположно направлению переносной скорости  .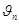

Сила трения в области высокого вакуума пропорциональна молекулярной концентрации или давлению газа. Уравнение (5) с учетом (6) можно преобразовать к следующему виду:

 , (9)

откуда видно, что сила трения возрастает пропорционально корню квадратному из абсолютной температуры.

В области среднего вакуума можно записать аппроксимирующее выражение. рассчитывая градиент переносной скорости в промежутке между поверхностями переноса по следующей формуле:

 ,

где 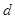 – расстояние между поверхностями переноса. Тогда с учетом (7) сила трения в области среднего вакуума:

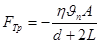 (8).

Легко заметить, что в условиях низкого вакуума при 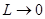 формула (8) с (2), а в условиях высокого вакуума при  с (9).

Зависимость от давления силы трения тонкой пластины площадью 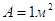 , движущейся в воздухе при  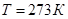со скоростью  , при расстояние между поверхностями переноса 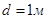 показана на рис 2.

Вязкость газов используется для измерения давлений в области среднего и высокого вакуума, однако вязкостные манометры не получили пока широкого применения из-за длительности регистрации давления. Гораздо шире явление вязкости используется в технологии получения вакуума. На этом принципе работают струйные эжекторные насосы, выпускаемые промышленностью для работы в области низкого вакуума.

При  , ,  , ,  .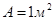

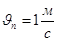Список литературы

Л.Н. Розанов. Вакуумная техника.

Москва «Высшая школа» 1990.

 

Поделиться:

Воспользуйтесь поиском по сайту: