 |
Замена переменной в дифференциале
|
|
|
|
Тема. Дифференциал функции. Замена переменной в дифференциале.
Занятие 1.
Напомним определение дифференциала функции.
Определение 1.1. Если 
есть производная от функции 
в точке 
, а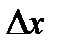 
произвольное приращение аргумента, то дифференциалом функции назовем произведение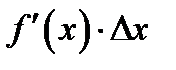 
. Дифференциал будем обозначать символами 
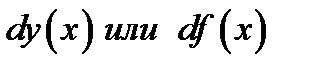. Таким образом
(1.1)
Замечание. Если положить 
, то
(1.2)
Ввиду (1.2) дифференциал от функции будем записывать далее
или 
(1.3)
Причем точка 
и величина 
не зависят друг от друга и задаются произвольно,
а производную функции можно записывать формулой
(1.4)
Так как дифференциал функции равен произведению производной функции на дифференциал аргумента, то формулы для дифференциалов те же, что и для производных, если каждую умножить на 
(1.5)
Таблица дифференциалов аналогична таблице производных.
Таблица дифференциалов
(1.6)
Инвариантность формулы дифференциала
Теорема 1.1. Вид формулы дифференциала функции не изменится, если аргумент функции заменить новой переменной.
Доказательство. Пусть нам дана функция 
, тогда согласно формуле (1.3) её дифференциал равен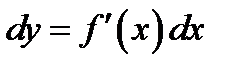 
, где 
независимая переменная. Если переменная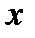 
сама становится зависимой 
. Тогда функция становится функцией, зависящей от переменной 
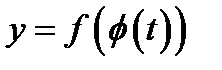
и её дифференциал будет равен 
.
Применяя цепное правило, получаем 
или
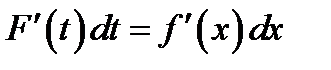(1.7)
Вывод. Для любой переменной 
формула дифференциала 
функции 
справедлива независимо от того является ли переменное 
независимым или оно есть функция другого независимого переменного.
Замена переменной в дифференциале
Операция замены переменной в дифференциале упрощает выражение дифференциала
Пример 1. В дифференциале 
заменить переменную 
по правилу 
.
|
|
|
Решение. Из условия задачи следует 
. Подставляя полученные данные в дифференциал, получаем 
;
Пример 2. В дифференциале 
заменить переменную по правилу 
.
Решение. Из условия задачи следует 
.
Подставляя полученные данные в дифференциал, получаем 
Пример 3. В дифференциале 
заменить переменную по правилу 
.
Решение. Из условия задачи следует 
; 
. Подставляя полученные данные в дифференциал, получаем 
;
Пример 4. В дифференциале 
заменить переменную по правилу 
;
Решение. В данном случае нужно использовать известные тригонометрические формулы 
Данная замена переменного называется универсальной тригонометрической подстановкой.
Подставляя полученные данные в дифференциал, получаем
;
Пример 5. В дифференциале 
заменить переменную по правилу ;
Решение. Применяя универсальную тригонометрическую подстановку, получаем 
;
Пример 6. В дифференциале 
заменить переменную по правилу 
;
Решение. В данном случае нужно использовать известные тригонометрические формулы
Из условия задачи следует 
Пример 7. В дифференциале 
заменить переменную по правилу 
;
Решение. Из условия задачи следует
Подставляя полученные данные в дифференциал, получаем 
;
Пример 8. В дифференциале 
заменить переменную по правилу 
.
Решение. Из условия задачи следует
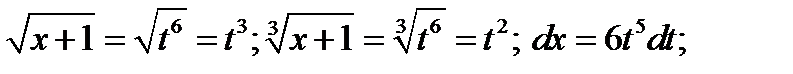
Подставляя полученные данные в дифференциал, получаем 
.
Помимо операции дифференцирования рассмотрим операцию обратную к ней
Пример 9. Рассмотрим следующую задачу. Найти функции, дифференциалы которых равны
следующим выражениям
Решение. 1) Из таблицы дифференциалов (1.6) следует, что 
.
Ответ.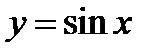 
2) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную 
по правилу 
. В результате получаем 
. Из таблицы (1.6)
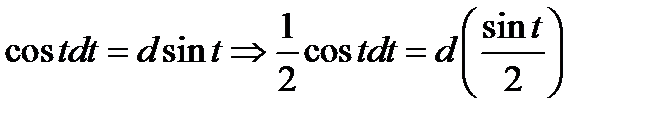. Откуда 
.
Ответ. 
.
3) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную по правилу 
. В результате получаем 
. Из таблицы (1.6) 
. Откуда 
.
|
|
|
Ответ. 
.
4) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную по правилу 
. В результате получаем 
. Из таблицы (1.6)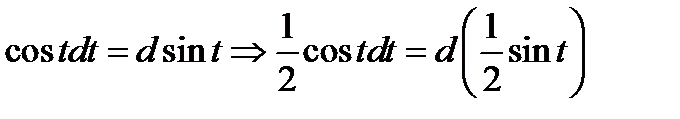 
. Откуда 
.
Ответ. 
.
5) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную по правилу 
. В результате получаем 
. Из таблицы (1.6) 
. Откуда 
.
Ответ. 
.
Самостоятельная работа.
Упражнение 1.1. Замените переменную в дифференциалах
Упражнение 1.2. Дифференциалами каких функций являются данные дифференциальные выражения
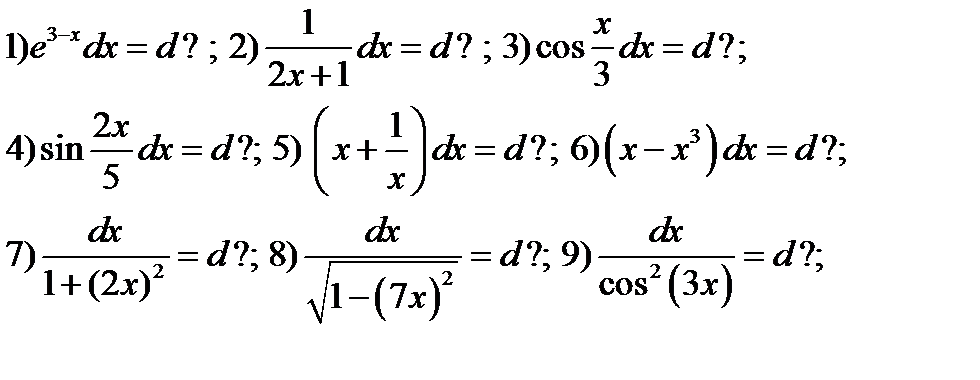
Указание. При решении упражнения 1.2 используйте таблицу дифференциалов (1.6) и решение примера 9.
|
|
|
