 |
Решение задачи на компьютере
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА №2
по мат.программированию
«Графический и симплексный методы решения ОЗЛП»
Для изготовления 2-х различных изделий А и В используется 3 вида сырья. На производство единицы изделия А требуется затратить сырья 1-го вида а1 кг, сырья 2-го вида – а2 кг, сырья 3-го вида – а3 кг. На производство единицы изделия В требуется затратить сырья 1-го вида в1 кг, сырья 2-го вида – в2 кг, сырья 3-го вида – в3 кг. Производство обеспечено сырьём 1-го вида в количестве Р1 кг, сырьём 2-го вида в количестве Р2 кг, сырьём 3-го вида в количестве Р3 кг. Прибыль от реализации единицы готового изделия А составляет  ден.ед., а изделия В –
ден.ед., а изделия В –  ден.ед.
ден.ед.
| № | а1 | а2 | а3 | в1 | в2 | в3 | Р1 | Р2 | Р3 |
|
|
| 8 | 11 | 7 | 8 | 10 | 5 | 6 | 425 | 450 | 550 | 2 | 4 |
Математическая модель задачи
Обозначим количество произведенной продукции 1-го вида через х1, 2-го вида – х2. Тогда линейная функция примет вид: Z (х1, х2) =2*х1+4*х2.
Это есть цена произведенной продукции. Наше решение должно обеспечить максимальное значение этой функции.
Условие налагает на величины х1 и х2 ограничения следующего вида:

Построенная линейная функция называется функцией цели и совместно системой ограничений образует математическую модель рассматриваемой экономической задачи.
Графическое решение задачи
Построим многоугольник решений. Для этого в системе координат х1Ох2 на плоскости изобразим граничные прямые
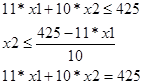


| х1 | 0 | 68,75 |
| х2 | 91,66 | 0 |
| х1 | 0 | 64,28 |
| х2 | 90 | 0 |
| х1 | 0 | 38,63 |
| х2 | 42,5 | 0 |
Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Многоугольником решений данной задачи является треугольник АОВ. Для построения прямой 2*х1+4*х2=0 строим радиус-вектор N =(2;4)=2.5*(2;4)=(5;10) и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z =0 перемещаем параллельно самой себе в направлении вектора N. Опорной по отношению к многоугольнику решений эта прямая становится в точке А (0;42,5), где функция Z принимает максимальное значение.
|
|
|
Оптимальный план задачи: х1=0; х2=42,5.
Подставляя значения х1 и х2 в линейную функцию, получаем Zmax =2*0+4*42.5=170 у.е.
Таким образом, для того чтобы получить максимальную прибыль в размере 170 у.е., необходимо запланировать производство 42,5 ед. продукции В.
Решение задачи симплексным методом
Запишем систему в векторной форме
х1*А1+х2*А2+х3*А3+х4*А4+х5*А5=Ао, где

Составляем симплексную таблицу.
| i | Базис | Сбаз | Ао | С1=2 | С2=4 | С3=0 | С4=0 | С5=0 | С.О. |
| А1 | А2 | А3 | А4 | А5 | |||||
| 1 | А3 | 0 | 425 | 11 | 10 | 1 | 0 | 0 | 42,5 |
| 2 | А4 | 0 | 450 | 7 | 5 | 0 | 1 | 0 | 90 |
| 3 | А5 | 0 | 550 | 8 | 6 | 0 | 0 | 1 | 91,66667 |
| m+1 | Zj-Cj | 0 | -2 | -4 | 0 | 0 | 0 |
| |
Среди полученных оценок имеются две отрицательные: Z1-C1=-2<0 и Z2-C2=-4<0. Это означает, что первоначальный опорный план не является оптимальным и его можно улучшить, включив в базис вектор, которому соответствует максимальное по модулю отрицательное число в m+1 строке. Разрешающий вектор-столбец А2. Разрешающий элемент находим по минимальному симплексному отношению. Разрешающий элемент – число 10.
Составим вторую симплексную таблицу.
| i | Базис | Сбаз | Ао | С1=2 | С2=4 | С3=0 | С4=0 | С5=0 |
| А1 | А2 | А3 | А4 | А5 | ||||
| 1 | А2 | 4 | 42,5 | 1,1 | 1 | 0,1 | 0 | 0 |
| 2 | А4 | 0 | 237,5 | 1,5 | 0 | -0,5 | 1 | 0 |
| 3 | А5 | 0 | 295 | 1,4 | 0 | -0,6 | 0 | 1 |
| m+1 | Zj-Cj | 170 | 2,4 | 0 | 0,4 | 0 | 0 | |
Просмотрев m+1 строку, убеждаемся, что опорный план – оптимален.
Оптимальный план предусматривает изготовление 42,5 ед.изделия В и не предусматривает изготовление изделий А. Изготовление изделий А привело бы к уменьшению прибыли на 2,4 у.е. Сырье 1-го вида используется полностью. Неиспользованными остается 450-237,5=212,5 тонн 2-го вида и 550-295=255 тонн 3-го вида сырья. Максимальная прибыль составляет 170 у.е.
|
|
|
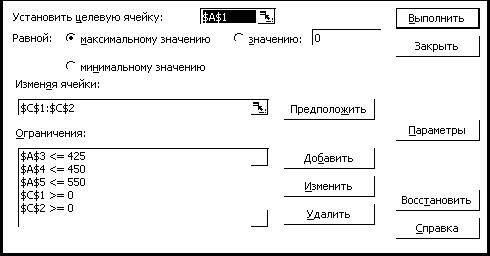
Решение задачи на компьютере
Выполним следующие действия:
– В ячейку А1 вводим формулу для целевой функции=2*х1+4*х2
– В ячейку А3 вводим формулу для ограничения: =11*с1+10*с2.
– В ячейку А4 вводим формулу для ограничения: =7*с1+5*с2.
– В ячейку А3 вводим формулу для ограничения: =8*с1+6*с2.
– В ячейку С1:С2 вводим начальные значения переменных (0:0).
–Выполним команду Сервис > Поиск решения.
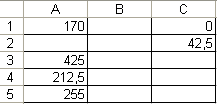
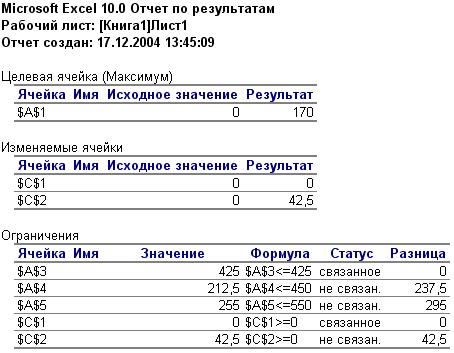
Следовательно, план выпуска продукции, включающий изготовление 42,5 изделий В является оптимальным. При данном плане выпуска изделий полностью используется сырье 1-го вида и остаётся неиспользованным 450-237,5=212,5 тонн 2-го вида и 550-295=255 тонн 3-го вида сырья, а стоимость производимой продукции равна 170 у.е.
ЛАБОРАТОРНАЯ РАБОТА №3
по мат.программированию
«Транспортная задача»
Имеются 3 пункта поставки однородного груза А1, А2, А3 и 5 пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1-А3 находится груз соответственно в количестве а1-а3 тонн. В пункты В1-В5 требуется доставить соответственно в1-в5 тонн груза. Стоимости перевозок 1 тонны груза между пунктами поставки и пунктами потребления приведены в матрице D. Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
| Пункты поставки | Пункты потребления | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 12 | 10 | 15 | 12 | 13 | 350 |
| А2 | 16 | 14 | 17 | 10 | 8 | 150 |
| А3 | 15 | 10 | 13 | 14 | 15 | 280 |
| Потребн. | 100 | 120 | 200 | 160 | 200 | |
|
|
|


