 |
Базовые преобразования в трехмерной области
|
|
|
|
Лучшим способом изучения формы объекта является помещение его в трехмерное пространство и выполнение операций вращения, масштабирования и построения его проекций. Распространим результаты для плоских изображений на трёхмерные изображения. Тогда точка Р в трехмерном пространстве в ОК представится вектором || x y z 1 || или при h¹1 для получения обычных трехмерных координат необходимо ОК нормализовать, т.е. разделить на h.
Преобразования в пространстве выполняются, как и для плоскости, а их усложнение связано с преобразованием произвольного поворота, которое выполняется комбинацией поворотов относительно трех осей.
Как и для плоскости определим матрицы основных преобразований.
Трехмерный перенос на вектор Т=|| tx ty tz || в матричной форме запишется в виде Р*=Р×М(Т), где
 .
.
Трехмерное масштабирование на вектор Е (еx, еy, еz) определяется как Р*= Р×М(Е), где

Полное масштабирование относительно начала координат

Трехмерный сдвиг выполняют недиагональные элементы верхней левой подматрицы 3х3 в матрице преобразования 4х4, т.е.

Трехмерные вращения
Выделяются три основных вида вращения:
1. Вокруг координатных осей.
2. Вокруг осей, проходящих через начало координат.
3. Вокруг произвольных осей.
Вращение вокруг произвольной оси, проходящей через начало координат.
Направление оси вращения, задаётся единичным вектором n=n1i+n2j+n3k, где n1=cosa, n2=cosb, n3=cosg (n1, n2, n3 – направляющие косинусы).
Если ось вращения проходит через начало координат и точку А(x1, y1, z1), то
 .
.
Модель сферы, помещенной в пространство так, чтобы ось вращения проходила через начало координат, даёт следующую матрицу вращения:

Трехмерные вращения вокруг координатных осей являются частными случаями обобщенной матрицы вращения.
|
|
|
Трехмерные вращения вокруг координатных осей
Матрица поворота вокруг оси Х на угол Q получается из M(R(Q)) при n1=1 и n2=n3=0:
 .
.
Матрица поворота вокруг оси Y на угол Q получается из M(R(Q)) при n2=1 и n1=n3=0:
 .
.
Матрица поворота вокруг оси Z на угол Q получается из M (R(Q)) при n3=1 и n2=n1=0:
 .
.
В матричной форме рассмотренные преобразования для точки P(x,y,z) запишутся в виде
P*=P´M(R(X,Q)); P*=P·M(R(Y,Q)); P*=P·M(R(Z,Q)).
Вращения вокруг осей, проходящих через начало координат, обобщим на случай трехмерного вращения вокруг произвольной оси.
Вращение вокруг произвольной оси. Процедура заключается в переносе изображения вместе с осью вращения, так чтобы ось вращения проходила через начало координат, выполнении вращения и операции обратного переноса в исходное положение. Тогда если ось вращения проходит через точку А = || k m n 1 ||, то преобразованные координаты определяются следующим выражением: P* = P M(Т(-А)) M(R(Q)) M(T(А)), откуда
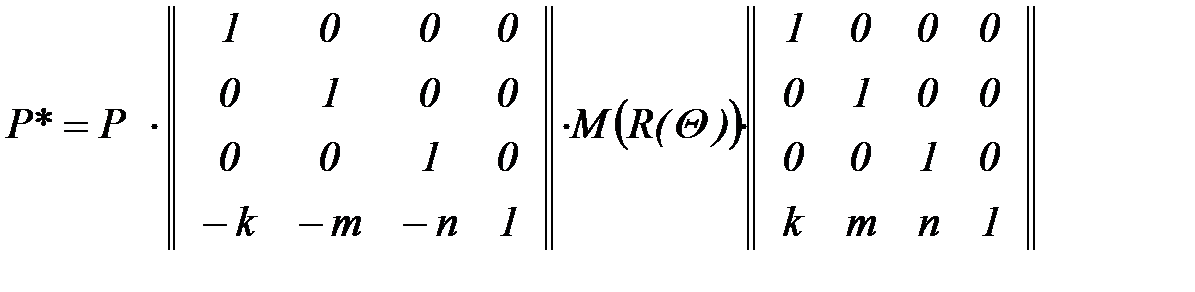 .
.
Таким образом, в матрице преобразования 4х4 для трехмерных ОК можно выделить 4 подматрицы.
Обобщённая матрица преобразований в ОК для трёхмерной области
 .
.
Подматрица 3х3 реализует сдвиг, масштабирование, отображение и вращения. Подматрица 1х3 реализует перенос, а подматрица 3х1 преобразование в перспективе. Элемент s выполняет общее изменение масштаба. Влияние подматрицы 3х1 на преобразование изображения рассмотрим в разделе «Проективная геометрия».
Примеры решения типовых задач
Задача 1. Прямая проходит через точки А(5,3) и В(6,8). К прямой применяется ОКП, заданное матрицей  с последующим проецированием на плоскость Н=1. Составить уравнение результирующей прямой.
с последующим проецированием на плоскость Н=1. Составить уравнение результирующей прямой.
Решение.
Запишем матрицу Р, задающую прямую в ОК  .
.
Найдём матрицу Р*, получающуюся после применения ОКП  .
.
Выполним операцию проецирования на плоскость Н=1. Для этого нормализуем полученные координаты  ,
,
|
|
|
т.е. получена прямая, проходящая через точки А *(0.65, 1.5) и В *(0.54, 1.57).
Запишем уравнение прямой А*В*
 ,
,
а уравнение прямой АВ:  .
.
т.е. мы трансформировали прямую  в
в  .
.
Задача 2. Найти матрицу ОКП, трансформирующую изображение, заданное матрицей Р в изображение, заданное матрицей Р *
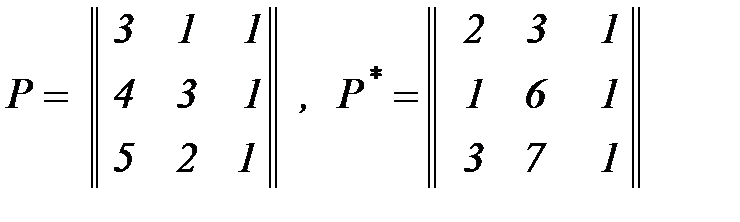 .
.
Решение: Р* = Р Т, откуда Т = Р-1 Р*.
1. Найдем определитель матрицы Р, разложив её по элементам первой строки
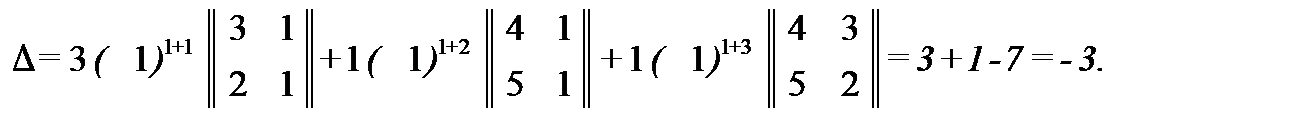
Найдём алгебраические дополнения каждого элемента матрицы Р

Из алгебраических дополнений составим матрицу А и после её транспонирования получим матрицу Аt
 .
.
Получим обратную матрицу  , после чего найдём матрицу
, после чего найдём матрицу  ;
;
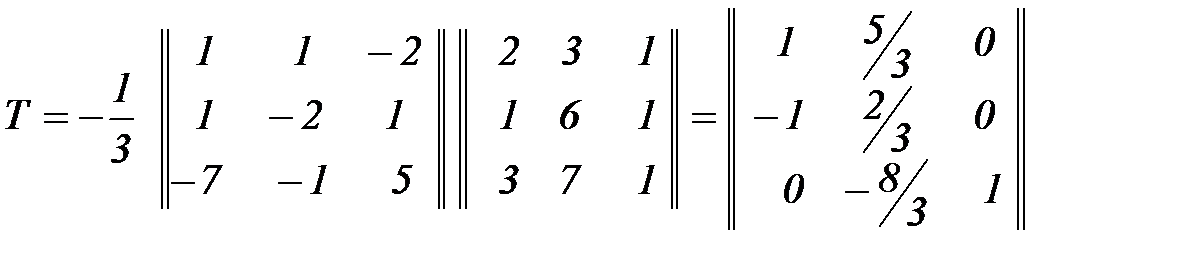 .
.
Выполним проверку правильности нахождения матрицы Т, т.е Р ´ Т = Р*:
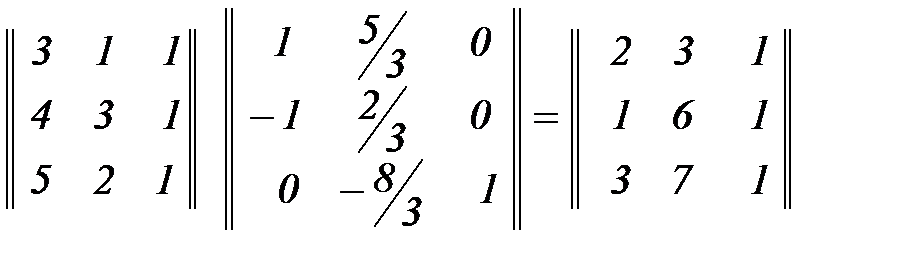 .
.
Задача 3. Составить матрицу ОКП, трансформирующего точку (x, y,z, 1) в точку ((x+5y+2z), (6x+y+4z), (2x+3y+z), 1)).
Решение. Запишем  ,
,
что возможно, исходя из правил перемножения матриц, когда матрица
 .
.
|
|
|


