Главная | Обратная связь | Поможем написать вашу работу!

Экзаменационные билеты по геометрии 10 класс

(2012-2013 учебный год)

Билет № 1

1. Правильные многогранники. Элементы симметрии правильных многогранников.

2. Докажите теорему о плоскости, перпендикулярной одной из двух параллельных прямых.

3. В тетраэдре ДАВС <ДАС=<ДАВ и <АДС=<АДВ. Докажите, что ВС АД.

4. Через сторону МО ромба МNPO проведена плоскость MOF так, что двугранный угол NMOF=45 градусов. Найдите сторону ромба, если угол NMO равен 30 градусов, а расстояние от точки N до плоскости MOF равно а см.

Билет № 2

1. Свойства прямоугольного параллелепипеда

2. Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости.

3. На плоскости лежат три точки А, В и С так, что АВ = 2, ВС = АС = . Точка О не принадлежит плоскости АВС и отстоит от точек А, В и С на расстояния
соответственно. Найдите расстояние от точки О до плоскости АВС.

4. В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 60°, а расстояние от середины стороны основания до противоположной боковой грани равно 4 . Найдите площадь боковой поверхности.

Билет № 3

1. Пространственная теорема Пифагора.

2. Параллельные плоскости. Признак параллельности двух плоскостей

3. АВСДА₁В₁С₁Д₁– куб. Чему равно расстояние между скрещивающимися прямыми

ДА₁ и СД₁

4. В правильной треугольной пирамиде высота основания равна 2 , а расстояние от

середины стороны основания до противоположного бокового ребра — 3 см. Найдите:

угол между боковыми гранями

Билет № 4

1. Теорема о прямой, перпендикулярной к плоскости

2. Параллелепипед. Теорема о точке пересечения диагоналей параллелепипеда.

3. Все ребра наклонной призмы АВСА₁В₁С₁, в основании которой лежит правильный треугольник, равны а. Точка А₁ равноудалена от А, В и С. Найдите расстояние
от вершины А₁ до плоскости ВСС₁ и угол, который составляет с этой плоскостью прямая А ₁С.

4. АВСДА1В1С1Д1 – куб. К середина А1Д1Найти двугранные углы а) АВВ1С

б) А1ВВ1К

Билет № 5

1. Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости.

2. Теоремы о боковой поверхности правильной пирамиды

3. В тетраэдре ДАВС ребро ДВ перпендикулярно плоскости АВС. <АСВ=90 градусов, ВС=ВД, точка F- середина АД. Постройте сечение тетраэдра плоскостью, проходящей через точку F и перпендикулярной СД.

4. В правильной треугольной пирамиде высота основания равна 2 , а расстояние от середины стороны основания до противоположного бокового ребра — 3 см. Найдите:

плоский угол при вершине пирамиды

Билет № 6

1. Аксиомы стереометрии. Теорема о существовании и единственности плоскости,

проходящей через данную прямую и точку, не принадлежащую этой прямой.

2. Теорема о площади проекции фигуры на плоскость.

3. АВСДА1В1С1Д1 – куб. К середина СС1. Найти расстояние между А 1С и Д1К

4. Основанием пирамиды ДАВС является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29 см, а катет АС равен 21 см. Боковое ребро ДА перпендикулярно к плоскости основания и равно 20 см. Найти площадь боковой поверхности пирамиды.

Билет № 7

Сформулируйте определение перпендикулярности двух плоскостей. Докажите признак перпендикулярности двух плоскостей.
Теорема о площади боковой поверхности наклонной призмы.

3. Для правильного тетраэдра АВС О с ребром а определите расстояние от точки К — середины ребра АС — до плоскости ВСО и угол между прямой КВ и этой плоскостью.

4. В прямом параллелепипеде АВСДА₁В₁С₁Д₁АВ=1, ВС = 7 , 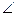АВС = 150°. Через диагональ АС и вершину В₁ проведена плоскость, составляющая с плоскостью основания угол в 60°. Найдите площадь боковой поверхности параллелепипеда.

Билет № 8

1. Докажите теорему, обратную теореме о трех перпендикулярах

2. Теорема о боковой поверхности призмы

3. АВСДА₁В₁С₁Д₁– куб. К середина СС_1. Найти расстояние между АС и Д₁К

4. В прямом параллелепипеде АВСДА₁В₁С₁Д₁СД=15, ВС =7, 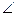ВСД = 60°. Через диагональ ВД и вершину С₁ проведена плоскость, составляющая с плоскостью основания угол в 45°. Найдите площадь боковой поверхности параллелепипеда.

Билет № 9

1. Теорема об отрезках параллельных прямых, заключенных между двумя параллельными плоскостями.

2. Докажите теорему о трех перпендикулярах

3. Через точку О пересечения диагоналей ромба АВСД проведена прямая ОМ так, что МА=МС, МВ=МД. Докажите, что прямая ОМ перпендикулярна к плоскости ромба.

4. АВСДА₁В₁С₁Д₁– куб. К середина СД_. Найти расстояние между АД и В₁К

Билет № 10

1. Свойства перпендикулярности прямой и плоскости

2. Теорема о плоскости, перпендикулярной одной из двух параллельных прямых.

3. Точка М равноудалена от всех вершин правильного треугольника со стороной 12 см и удалена от плоскости треугольника на расстояние 6 см. Найдите расстояние от точки М до сторон треугольника.

плоский угол при вершине пирамиды

Билет № 11

1. Докажите теорему о трех перпендикулярах.

2. Параллелепипед. Свойство противолежащих граней параллелепипеда

3. Найдите расстояния и углы между диагональю АС₁ куба АВСДА₁В₁С₁Д₁ и скрещивающимися с ней диагоналями граней этого куба, если ребро куба равно 1.

4. В треугольнике АВС АС=СВ=8, 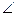АСВ=130 градусов. Точка М удалена от плоскости АВС на расстояние, равное 12, и находится на равном расстоянии от вершин треугольника АВС. Найдите угол между МА и плоскостью АВС

Билет № 12

1. Параллельные плоскости (определение). Признак параллельности двух плоскостей.

2. Докажите, что если плоскости и перпендикулярны прямой а, то они параллельны.

3. Внутри двугранного угла величины ( < 90°) взята точка М, удаленная от граней двугранного угла на а и b соответственно. Найдите расстояние от М до ребра двугранного угла.

4. Треугольник АВС- равнобедренный, АВ=АС, точка Д – середина ВС, прямая ЕД перпендикулярна плоскости АВС. Докажите, что АЕ перпендикулярна ВС.

Билет № 13

1. Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости.

2. Теорема о линиях пересечения двух параллельных плоскостей третьей плоскостью.

Из точки к плоскости проведены две наклонные длиной 12 и 24 см, проекции которых относятся как 1:7. Найдите расстояние от точки до плоскости.
В параллелепипеде АВСДА1В1С1Д1точки Р и К - середины АВ и ВС соответсвенно, А1С=АС1. Найдите угол между прямыми ДД1и РК.

Билет № 14

1. Теорема о плоскости, перпендикулярной одной из двух параллельных прямых.

2. Сформулируйте определение перпендикулярности двух плоскостей. Докажите признак перпендикулярности двух плоскостей.

3. Из центра О правильного треугольника АВС проведен перпендикуляр ОМ к его плоскости. Найдите площадь треугольника МВС, если АВ=6 см, ОМ=4см.

4. В трехгранном угле ОАВС все плоские углы равны 60°. Какой угол
с плоскостью ВОС составляет ребро ОА?

Билет № 15

1. Прямая, параллельная плоскости (определение). Признак параллельности прямой и плоскости.

2. Параллелепипед. Свойство противолежащих граней параллелепипеда.

3. Из вершины А правильного треугольника АВС проведен перпендикуляр АМ к его плоскости. Найти расстояние от точки М до стороны ВС, если АВ=4см, АМ=2 см.

4. В трехгранном угле плоские углы равны 120°; 120° и 90°. Найдите
двугранный угол, лежащий против меньшего плоского угла.

Билет № 16

1. Параллельные прямые (определение). Теорема о существовании и единственности прямой, параллельной данной прямой и проходящей через точку, не лежащую на этой прямой.

2. Двугранный угол. Линейный угол двугранного угла.

3. Из вершины Д квадрата АВСД проведен перпендикуляр ДМ к плоскости квадрата. Определите площадь треугольника МВС, если АД=8см, МД=6см.

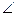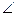4. В трехгранном угле ОАВС АОС = АОВ; 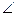ВОС = 90°. Ребро ОА составляет с плоскостью противолежащего плоского угла угол 45°. Найдите равные плоские углы.

Воспользуйтесь поиском по сайту: