 |
Проверка гипотезы о равенстве средних
|
|
|
|
Используется для проверки предложения о том, что среднее значения двух показателей, представленных выборками, значимо различаются. Существует три разновидности критерия: один – для связанных выборок, и два для несвязных выборок (с одинаковыми и разными дисперсиями). Если выборки не связны, то предварительно нужно проверить гипотезу о равенстве дисперсий, чтобы определить, какой из критериев использовать. Так же как и в случае сравнения дисперсий имеются 2 способа решения задачи, которые рассмотрим на примере.
ПРИМЕР 3. имеются данные о количестве продаж товара в двух городах. Проверить на уровне значимости 0,01 статистическую гипотезу о том, что среднее число продаж товара в городах различно.
| 23 | 25 | 23 | 22 | 23 | 24 | 28 | 16 | 18 | 23 | 29 | 26 | 31 | 19 |
| 22 | 28 | 26 | 26 | 35 | 20 | 27 | 28 | 28 | 26 | 22 | 29 |
Используем пакет «Анализ данных». В зависимости от типа критерия выбирается один из трех: «Парный двухвыборочный t-тест для средних» - для связных выборок, и «Двухвыборочных t-тест с одинаковыми дисперсиями» или «Двухвыборочных t-тест с разными дисперсиями» - для несвязных выборок. Вызовите тест с одинаковыми дисперсиями, в открывшемся окне в полях «Интервал переменной 1» и «Интервал переменной 2» вводят ссылки на данные (А1-N1 и А2-L2, соответственно), если имеются подписи данных, то ставят флажок у надписи «Метки» (у нас их нет, поэтому флажок не ставится). Далее вводят уровень значимости в поле «Альфа» - 0,01. Поле «Гипотетическая средняя разность» оставляют пустыми. В разделе «Параметры вывода» ставят метку около «Выходной интервал» и поместив курсор в появившемся поле напротив надписи, щелкают левой кнопкой в ячейке В7. вывод результата будет осуществляться начиная с этой ячейки. Нажав на «ОК» появляется таблица результата. Сдвиньте границу между столбцами В и С, С и D, D и Е увеличив ширину столбцов В, С и D так, чтобы умещались все надписи. Процедура выводит основные характеристики выборки, t-статистику, критические значения этих статистик и критические уровни значимости «Р(Т<=t) одностороннее» и «Р(Т<=t) двухстороннее». Если по модулю t-статистика меньше критического, то средние показатели с заданной вероятностью равны. В нашем случае│-1,784242592│ < 2,492159469, следовательно, среднее число продаж значимо не отличается. Следует отметить, что если взять уровень значимости α=0,05, то результаты исследования будут совсем иными.
|
|
|
Двухвыборочный t-тест с одинаковыми дисперсиями | ||
|
|
|
|
| город 1 | город 2 | |
| Среднее | 23,57142857 | 26,41666667 |
| Дисперсия | 17,34065934 | 15,35606061 |
| Наблюдения | 14 | 12 |
| Объединенная дисперсия | 16,43105159 |
|
| Гипотетическая разность средних | 0 |
|
| df | 24 |
|
| t-статистика | -1,784242592 |
|
| P(T<=t) одностороннее | 0,043516846 |
|
| t критическое одностороннее | 2,492159469 |
|
| P(T<=t) двухстороннее | 0,087033692 |
|
| t критическое двухстороннее | 2,796939498 |
|
Лабораторная работа №3
ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
Цель: Освоить методы построения линейного уравнения парной регрессии с помощью ЭВМ, научиться получать и анализировать основные характеристики регрессионного уравнения.
Рассмотрим методику построения регрессионного уравнения на примере.
ПРИМЕР. Даны выборки факторов х i и у i. По этим выборкам найти уравнение линейной регрессии ỹ = ах + b. Найти коэффициент парной корреляции. Проверить на уровне значимости а = 0,05 регрессионную модель на адекватность.
| Х | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 6,7 | 6,3 | 4,4 | 9,5 | 5,2 | 4,3 | 7,7 | 7,1 | 7,1 | 7,9 |
Для нахождения коэффициентов a и b уравнения регрессии служат функции НАКЛОН и ОТРЕЗОК, категории «Статистические». Вводим в А5 подпись «а=» а в соседнюю ячейку В5 вводим функцию НАКЛОН, ставим курсор в поле «Изв_знач_у» задаем ссылку на ячейки В2-K2, обводя их мышью. Результат 0,14303. Найдем теперь коэффициент b. Вводим в А6 подпись «b=», а в В6 функцию ОТРЕЗОК с теми же параметрами, что и функции НАКЛОН. Результат 5,976364. следовательно, уравнение линейной регрессии есть у=0,14303х+5,976364.
|
|
|
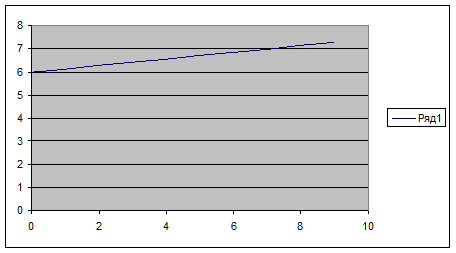
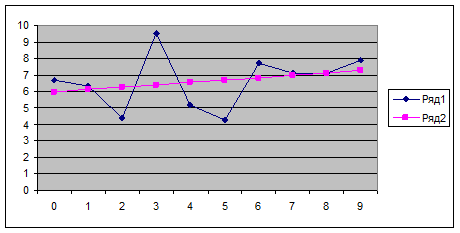
Построим график уравнения регрессии. Для этого в третью строчку таблицы введем значения функции в заданных точках Х (первая строка) – у(х1). Для получения этих значений используются функция ТЕНДЕНЦИЯ категории «Статистические». Вводим в А3 подпись «Y(X) и, поместив курсор в В3, вызываем функцию ТЕНДЕНЦИЯ. В полях «Изв_знач_у» и «Изв_знач_х» даем ссылку на В2-K2 и В1-K1. в поле «Нов_знач_х» вводим также ссылку на В1-K1. в поле «Константа» вводят 1, если уравнение регрессии имеет вид y = ax + b, и 0, если у=ах. В нашем случае вводим единицу. Функция ТЕНДЕНЦИЯ является массивом, поэтому для вывода всех ее значений выделяем область В3-K3 и нажимаем F2 и Ctrl+Shift+Enter. Результат – значения уравнения регрессии в заданных точках. Строим график. Ставим курсор в любую свободную клетку, вызываем мастер диаграмм, выбираем категорию «Точеная», вид графика – линия без точек (в нижнем правом углу), нажимаем «Далее», в поле «Диагноз» вводим ссылку на В3-K3. переходим на закладку «Ряд» и в поле «Значения Х» вводим ссылку на В1-K1, нажимаем «Готово». Результат – прямая линия регрессии. Посмотрим, как различаются графики опытных данных и уравнения регрессии. Для этого ставим курсор в любую свободную ячейку, вызываем мастер диаграмм, категория «График», вид графика – ломанная линия с точками (вторая сверху левая), нажимаем «Далее», в поле «Диапазон» вводим ссылку на вторую и третью строки В2-K3. переходим на закладку «Ряд» и в поле «Подписи оси Х» вводим ссылку на В1-K1, нажимаем «Готово». Результат – две линии (Синяя – исходные, красная – уравнение регрессии). Видно, что линии мало различаются между собой.
| а= | 0,14303 |
| b= | 5,976364 |
Для вычисления коэффициента корреляции rxy служит функция ПИРСОН. Размещаем график так, чтобы они располагались выше 25 строки, и в А25 делаем подпись «Корреляция», в В25 вызываем функцию ПИРСОН, в полях которой «Массив 2» вводим ссылку на исходные данные В1-K1 и В2-K2. результат 0,993821. коэффициент детерминации Rxy – это квадрат коэффициента корреляции rxy. В А26 делаем подпись «Детерминация», а в В26 – формулу «=В25*В25». Результат 0,265207.
|
|
|
Однако, в Excel существует одна функция, которая рассчитывает все основные характеристики линейной регрессии. Это функция ЛИНЕЙН. Ставим курсор в В28 и вызываем функцию ЛИНЕЙН, категории «Статистические». В полях «Изв_знач_у» и «Изв_знач_х» даем ссылку на В2-K2 и В1-K1. поле «Константа» имеет тот же смысл, что и функции ТЕНДЕНЦИЯ, у нас она равна 1. поле «Стат» должно содержать 1, если нужно вывести полную статистику о регрессии. В нашем случае ставим туда единицу. Функция возвращает массив размеров 2 столбца и 5 строк. После ввода выделяем мышью ячейку В28-С32 и нажимаем F2 и Ctrl+Shift+Enter. Результат – таблица значений, числа в которой имеют следующий смысл:
| Коэффициент а | Коэффициент b |
| Стандартная ошибка m o | Стандартная ошибка mh |
| Коэффициент детерминации Rxy | Среднеквадратическое отклонение у |
| F – статистика | Степени свободы n-2 |
| Регрессионная сумма квадратов Sn2 | Остаточная сумма квадратов Sn2 |
| 0,14303 | 5,976364 |
| 0,183849 | 0,981484 |
| 0,070335 | 1,669889 |
| 0,60525 | 8 |
| 1,687758 | 22,30824 |
Анализ результата: в первой строчке – коэффициенты уравнения регрессии, сравните их с рассчитанными функциями НАКЛОН и ОТРЕЗОК. Вторая строчка – стандартные ошибки коэффициентов. Если одна из них по модулю больше, чем сам коэффициент, то коэффициент считается нулевым. Коэффициент детерминации характеризует качество связи между факторами. Полученное значение 0,070335 говорит об очень хорошей связи факторов, F – статистика проверяет гипотезу о адекватности регрессионной модели. Данное число нужно сравнить с критическим значением, для его получения вводим в Е33 подпись «F-критическое», а в F33 функцию FРАСПОБР, аргументами которой вводим соответственно «0,05» (уровень значимости), «1» (число факторов Х) и «8» (степени свободы).
| F-критическое | 5,317655 |
Видно, что F-статистика меньше, чем F-критическое, значит, регрессионная модель не адекватна. В последней строке приведены регрессионная сумма квадратов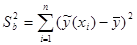 
и остаточные суммы квадратов 
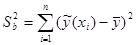. Важно, чтобы регрессионная сумма (объясненная регрессией) была намного больше остаточной (не объясненная регрессией, вызванная случайными факторами). В нашем случае это условие не выполняется, что говорит о плохой регрессии.
|
|
|
Вывод: В ходе работы я освоил методы построения линейного уравнения парной регрессии с помощью ЭВМ, научился получать и анализировать основные характеристики регрессионного уравнения.
Лабораторная работа № 4
НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Цель: освоить методы построения основных видов нелинейных уравнений парной регрессии с помощью с помощью ЭВМ (внутренне линейные модели), научиться получать и анализировать показатели качества регрессионных уравнений.
Рассмотрим случай, когда нелинейные модели с помощью преобразования данных можно свести к линейным (внутренне линейные модели).
ПРИМЕР. Построить уравнение регрессии у = f (х) для выборки хп уп (f = 1,2,…,10). В качестве f (х) рассмотреть четыре типа функций – линейная, степенная, показательная и гиперболу:
у = Ах + В; у = АхВ; у = АеВх; у = А/х + В.
Необходимо найти их коэффициенты А и В, и сравнив показатели качества, выбрать функцию, которая наилучшим образом описывает зависимость.
| Прибыль Y | 0,3 | 1,2 | 2,8 | 5,2 | 8,1 | 11,0 | 16,8 | 16,9 | 24,7 | 29,4 |
| Прибыль X | 0,25 | 0,50 | 0,75 | 1,00 | 1,25 | 1,50 | 1,75 | 2,00 | 2,25 | 2,50 |
Введем данные в таблицу вместе с подписями (ячейки A1-K2). Оставим свободными три строчки ниже таблицы для ввода преобразованных данных, выделим первые пять строк, проведя по левой серой границе по числам от 1 до 5 и выбрать какой-либо цвет (светлый – желтый или розовый) раскрасить фон ячеек. Далее, начиная с A6, выводим параметры линейной регрессии. Для этого в ячейку A6 делаем подпись «Линейная» и в соседнюю ячейку B6 вводим функцию ЛИНЕЙН. В полях «Изв_знач_x» даем ссылку на B2-K2 и B1-K1, следующие два поля принимают значения по единице. Далее обводим область ниже в 5 строчек и левее в 2 строки и нажимаем F2 и Ctrl+Shift+Enter. Результат - таблица с параметрами регрессии, из которых наибольший интерес представляет коэффициент детерминации в первом столбце третий сверху. В нашем случае он равен R1 = 0,951262. Значение F-критерия, позволяющего проверить адекватность модели F1 = 156,1439
(четвертая строка, первый столбец). Уравнение регрессии равно
y = 12,96 x +6,18 (коэффициенты a и b приведены в ячейках B6 и C6).
| Линейная | 12,96 | -6,18 | ||
|
| 1,037152 | 1,60884 | ||
|
| 0,951262 | 2,355101 | ||
|
| 156,1439 | 8 | ||
|
| 866,052 | 44,372 |
Определим аналогичные характеристики для других регрессий и в результате сравнения коэффициентов детерминации найдем лучшую регрессионную модель. Рассмотрим гиперболическую регрессию. Для ее получения преобразуем данные. В третьей строке в ячейку A3 введем подпись «1/ x» а в ячейку B3 введем формулу «=1/B2». Растянем автозаполнением данную ячейку на область B3-K3. Получим характеристики регрессионной модели. В ячейку А12 введем подпись «Гипербола», а в соседнюю функцию ЛИНЕЙН. В полях «Изв_знач_ y» и «Изв_знач_ x 2 даем ссылку на B1-K1 и преобразованные данные аргумента x – B3-K3, следующие два поля принимают значения по единице. Далее обводим область ниже 5 строчек и левее в 2 строки и нажимаем F2 и Ctrl+Shift+Enter. Получаем таблицу параметров регрессии. Коэффициент детерминации в данном случае равен R2 = 0,475661, что намного хуже, чем в случае линейной регрессии. F-статистика равна F2 = 7,257293. Уравнение регрессии равно y = -6,25453 x 18,96772.
| Гипербола | -6,25453 | 18,96772 |
|
| 2,321705 | 3,655951 |
|
| 0,475661 | 7,724727 |
|
| 7,257293 | 8 |
|
| 433,0528 | 477,3712 |
Рассмотрим экспоненциальную регрессию. Для ее линеаризации получаем уравнение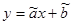 
, где ỹ = ln y, ã = b, 
= ln a. Видно, что надо сделать преобразование данных – y заменить на ln y. Ставим курсор в ячейку А4 и делаем заголовок «ln y». Ставим курсор в В4 и вводим формулу LN (категория «Математические»). В качестве аргумента делаем ссылку на В1. Автозаполнением распространяем формулу на четвертую строку на ячейки В4-K4. Далее в ячейке F6 задаем подпись «Экспонента» и в соседней G6 вводим функцию ЛИНЕЙН, аргументами которой будут преобразованные данные В4-K4 (в поле «Изв_знач_ y»), а остальные поля такие же как и для случая линейной регрессии (B2-K2, 1, 1). Далее обводим ячейки G6-H10 и нажимаем F2 и Ctrl+Shift+Enter. Результат R3 = 0,89079, F3 = 65,25304, что говорит об очень хорошей регрессии. Для нахождения коэффициентов уравнения регрессии b = ã; 
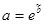ставим курсор в J6 и делаем заголовок «а=», а в соседней К6 формулу «=ЕХР(Н6)», в J7 даем заголовок «b=», а в К7 формулу «=G6». Уравнение регрессии есть y = 0,511707· e 6,197909x.
| Экспонента | 1,824212 | -0,67 |
| a= | 0,511707 |
|
| 0,225827 | 0,350304 |
| b= | 6,197909 |
|
| 0,89079 | 0,512793 |
|
|
|
|
| 65,25304 | 8 |
|
|
|
|
| 17,15871 | 2,103652 |
|
|
|
Рассмотрим степенную регрессию. Для ее линеаризации получаем уравнение ỹ = ã 
, где ỹ = ln y,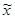 
= ln x, ã = b, = ln a. Видно, что надо сделать преобразование данных – y заменить на ln y и x заменить на ln x. Строчка с ln y у нас уже есть. Преобразуем переменные х. В ячейку А5 даем подпись «ln x», а в В5 и вводим формулу LN (категория «Математические»). В качестве аргумента делаем ссылку на В2. Автозаполнением распространяем формулу на пятую строку на ячейки B5-K5. Далее в ячейке F12 задаем подпись «Степенная» и в соседней G12 вводим функцию ЛИНЕЙН, аргументами которой будут преобразованные данные B4-K4 (в поле «Изв_знач_ у»), и B5-K5 (в поле «Изв_знач_ х»), остальные поля – единицы. Далее освободим ячейки G12-H16 и нажимаем F2 и Ctrl+Shift+Enter. Результат R4 = 0,997716, F4 = 3494,117, что говорит об хорошей регрессии. Для нахождения коэффициентов уравнения регрессии b = ã; 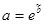ставим курсор в J12 и делаем заголовок «а=», а в соседней К12 формулу «=ЕХР(Н12)», в J13 даем заголовок «b=», а в К13 формулу «=G12». Уравнение регрессии есть у = 4,90767/ х + 7,341268.
| Степенная | 1,993512 | 1,590799 |
| a= | 4,90767 |
|
| 0,033725 | 0,023823 |
| b= | 7,341268 |
|
| 0,997716 | 0,074163 |
|
|
|
|
| 3494,117 | 8 |
|
|
|
|
| 19,21836 | 0,044002 |
|
|
|
Проверим, все ли уравнения адекватно описывают данные. Для этого нужно сравнить F-статистики каждого критерия с критическим значением. Для его получения вводим в А21 подпись «F-критическое», а в В21 функцию FРАСПОБР, аргументами которой вводим соответственно «0,05» (уровень значимости), «1» (число факторов Х в строке «Уровень значимости 1») и «8» (степень свободы 2 = n – 2). Результат 5,317655. F – критическое больше F – статистики значит модель адекватна. Также адекватны и остальные регрессии. Для того, чтобы определить, какая модель наилучшим образом описывает данные, сравним индексы детерминации для каждой модели R 1, R 2, R 3, R 4. Наибольшим является R4 = 0,997716. Значит опытные данные лучше описывать у = 4,90767/ х+ 7,341268.
Вывод: В ходе работы я освоил методы построения основных видов нелинейных уравнений парной регрессии с помощью с помощью ЭВМ (внутренне линейные модели), научился получать и анализировать показатели качества регрессионных уравнений.
| Y | 0,3 | 1,2 | 2,8 | 5,2 | 8,1 | 11 | 16,8 | 16,9 | 24,7 | 29,4 |
| X | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 | 2,25 | 2,5 |
| 1/x | 4 | 2 | 1,333333 | 1 | 0,8 | 0,666667 | 0,571429 | 0,5 | 0,444444 | 0,4 |
| ln y | -1,20397 | 0,182322 | 1,029619 | 1,648659 | 2,0918641 | 2,397895 | 2,821379 | 2,827314 | 3,206803 | 3,380995 |
| ln x | -1,38629 | -0,69315 | -0,28768 | 0 | 0,2231436 | 0,405465 | 0,559616 | 0,693147 | 0,81093 | 0,916291 |
| Линейная | 12,96 | -6,18 |
|
| Экспонента | 1,824212 | -0,67 |
| a= | 0,511707 |
|
| 1,037152 | 1,60884 |
|
|
| 0,225827 | 0,350304 |
| b= | 6,197909 |
|
| 0,951262 | 2,355101 |
|
|
| 0,89079 | 0,512793 |
|
|
|
|
| 156,1439 | 8 |
|
|
| 65,25304 | 8 |
|
|
|
|
| 866,052 | 44,372 |
|
|
| 17,15871 | 2,103652 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Гипербола | -6,25453 | 18,96772 |
|
| Степенная | 1,993512 | 1,590799 |
| a= | 4,90767 |
|
| 2,321705 | 3,655951 |
|
|
| 0,033725 | 0,023823 |
| b= | 7,341268 |
|
| 0,475661 | 7,724727 |
|
|
| 0,997716 | 0,074163 |
|
|
|
|
| 7,257293 | 8 |
|
|
| 3494,117 | 8 |
|
|
|
|
| 433,0528 | 477,3712 |
|
|
| 19,21836 | 0,044002 |
|
|
|
| F - критическое | 5,317655 | |||||||||
|
|
| |||||||||
Лабораторная работа № 5
ПОЛИНОМИНАЛЬНАЯ РЕГРЕССИЯ
Цель: По опытным данным построить уравнение регрессии вида у = ах2 + b х + с.
ХОД РАБОТЫ:
Рассматривается зависимость урожайности некоторой культуры у i от количества внесенных в почву минеральных удобрений х i. Предполагается, что эта зависимость квадратичная. Необходимо найти уравнение регрессии вида ỹ = ах2 + bx + c.
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 29,8 | 58,8 | 72,2 | 101,5 | 141 | 135,1 | 156,6 | 181,7 | 216,6 | 208,2 |
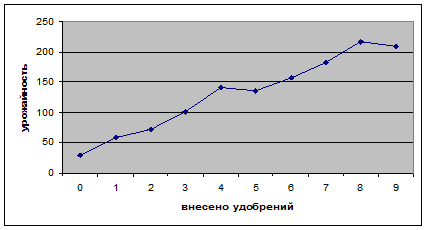
Введем эти данные в электронную таблицу вместе с подписями в ячейки А1-K2. Построим график. Для этого обведем данные Y (ячейки В2-K2), вызываем мастер диаграмм, выбираем тип диаграммы «График», вид диаграммы – график с точками (второй сверху левый), нажимаем «Далее», переходим на закладку «Ряд» и в поле «Подписи оси Х» делаем ссылку на В2-K2, нажимаем «Готово». График можно приблизить полиномом 2 степени у = ах2 + b х + с. Для нахождения коэффициентов a, b, c нужно решить систему уравнений:
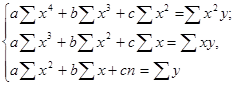
Рассчитаем суммы. Для этого в ячейку А3 вводим подпись «Х^2», а в В3 вводим формулу «= В1*В1» и Автозаполнением переносим ее на всю строку В3-K3. В ячейку А4 вводим подпись «Х^3», а в В4 формулу «=В1*В3» и Автозаполнением переносим ее на всю строку В4-K4. В ячейку А5 вводим «Х^4», а в В5 формулу «=В4*В1», автозаполняем строку. В ячейку А6 вводим «Х*Y», а в В8 формулу «=В2*В1», автозаполняем строку. В ячейку А7 вводим «Х^2*Y», а в В9 формулу «=В3*В2», автозаполняем строку. Теперь считаем суммы. Выделяем другим цветом столбец L, щелкнув по заголовку и выбрав цвет. В ячейку L1 помещаем курсор и щелкнув по кнопке автосуммы со значком ∑, вычисляем сумму первой строки. Автозаполнением переносим формулу на ячейки L1-710.
Решаем теперь систему уравнений. Для этого вводим основную матрицу системы. В ячейку А13 вводим подпись «А=», а в ячейки матрицы В13-D15 вводим ссылки, отраженные в таблице
| B | C | D | |
| 13 | =L5 | =L4 | =L3 |
| 14 | =L3 | =L2 | =L1 |
| 15 | =L2 | =L1 | =9 |
Вводим также правые части системы уравнений. В G13 вводим подпись «В=», а в Н13-Н15 вводим, соответственно ссылки на ячейки «=L7», «=L6», «=L2». Решаем систему матричным методом. Из высшей математики известно, что решение равно А-1В. Находим обратную матрицу. Для этого в ячейку J13 вводим подпись «А обр.» и, поставив курсор в K13 задаем формулу МОБР (категория «Математические»). В качестве аргумента «Массив» даем ссылку на ячейки В13:D15. Результатом также должна быть матрица размером 4×4. Для ее получения обводим ячейки K13-М15 мышью, выделяя их и нажимаем F2 и Ctrl+Shift+Enter. Результат – матрица А -1. Найдем теперь произведение этой матрицы на столбец В (ячейки Н13-Н15). Вводим в ячейку А18 подпись «Коэффициенты» и в В18 задаем функцию МУМНОЖ (категория «Математические»). Аргументами функции «Массив 1» служит ссылка на матрицу А -1 (ячейки K13-М15), а в поле «Массив 2» даем ссылку на столбец В (ячейки Н13-Н16). Далее выделяем В18-В20 и нажимаем F2 и Ctrl+Shift+Enter. Получившийся массив – коэффициенты уравнения регрессии a, b, c. В результате получаем уравнение регрессии вида: у = 1,201082 х 2 – 5,619177 х + 78,48095.
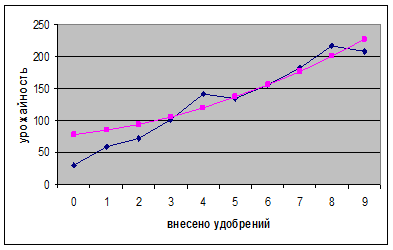
Построим графики исходных данных и полученных на основе уравнения регрессии. Для этого в ячейку А8 вводим подпись «Регрессия» и в В8 вводим формулу «=$В$18*В3+$В$19*В1+$В$20». Автозаполнением переносим формулу в ячейки В8-K8. Для построения графика выделяем ячейки В8-K8 и, удерживая клавишу Ctrl, выделяем также ячейки В2-М2. Вызываем мастера диаграмм, выбираем тип диаграммы «График», вид диаграммы – график с точками (второй сверху левый), нажимаем «Далее», переходим на закладку «Ряд» и в поле «Подписи оси Х» делаем ссылку на В2-М2, нажимаем «Готово». Видно, что кривые почти совпадают.
ВЫВОД: в процессе работы я по опытным данным научился строить уравнение регрессии вида у = ах2 + bх + с.
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| y | 29,8 | 58,8 | 72,2 | 101,5 | 141 | 135,1 | 156,6 | 181,7 | 216,6 | 208,2 | |||
| X^2 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | |||
| X^3 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | |||
| X^4 | 0 | 1 | 16 | 81 | 256 | 625 | 1296 | 2401 | 4096 | 6561 | |||
| X*Y | 0 | 58,8 | 144,4 | 304,5 | 564 | 675,5 | 939,6 | 1271,9 | 1732,8 | 1873,8 | |||
| X^2*Y | 0 | 58,8 | 288,8 | 913,5 | 2256 | 3377,5 | 5637,6 | 8903,3 | 13862,4 | 16864,2 | |||
| Регресс. | 78,48095 | 85,30121 | 94,52364 | 106,1482 | 120,175 | 136,6039 | 155,435 | 176,6682 | 200,3036 | 226,3412 | |||
| A= | 15333 | 2025 | 285 | B= | 52162,1 | A Обр. | 0,003247 | -0,03247 | 0,059524 | ||||
|
| 2025 | 285 | 45 | 7565,3 | -0,03247 | 0,341342 | -0,67857 | ||||||
|
| 285 | 45 | 9 | 1301,5 | 0,059524 | -0,67857 | 1,619048 | ||||||
| Коэффиц. | 1,201082 | a | |||||||||||
|
| 5,619177 | b | |||||||||||
|
| 78,48095 | c | |||||||||||
|
|
|
12 |
