Метод электрической корреляции.

Физические основы метода. В основе метода электрических корреляций (МЭК) лежат принципы одного из методов электроразведки на постоянном токе - метода заряженного тела (МЗ).

Если проводящий объект (в идеальном случае - с бесконечно большой проводимостью, т.е. с нулевым сопротивлением), находящегося в непрово­дящей среде, зарядить с помощью внешнего источника, то вокруг этого объ­екта будет создано электрическое поле (рис.1).

 

Рис.1. Распределение зарядов на поверхности проводящих объектов, эквипотенциальные линии вокруг этих объектов и графики потенциалов в окружающем пространстве для двух проводящих объектов: а – сферы, б – сфероида. 1 – изолинии и значения потенциалов; 2 – скважины, прошедшие через центр проводящего тела и точки заряда (ТЗ); 3 – заряды на поверхности тел; 4 – графики потенциалов вне проводящих тел.

 

При заряде проводящей сферы (рис.1а) потенциалы на поверхности ее будут равны потенциалу заряда, т.к. при нулевом сопротивлении сферы по­терь потенциалов внутри сферы не будет. Изометричная форма объекта при­во­дит к тому, что на поверхности его заряды будут распределены равномер­но, и эквипотенциальные линии в непроводящей среде (или в среде с боль­шим сопротивлением) будут представлять, в двумерном варианте, окружнос­ти. Т.к. потенциал точечного источника в однородной среде убывает обратно пропорционально расстоянию, то и радиусы эквипотенциальных окружнос­тей от данного тела, будут убывать по этому же закону. Перпендикуляр, опу­щенный из максимума графика потенциалов на ось измерения, в данном слу­чае, будет направлен к центру заряженного тела (точке заряда).

При заряде проводящего сфероида (рис.1б), вследствие электро­стати­че­с­кого взаимодействия, заряды будут смещаться в сторону полюсов сфероида, что скажется на распределении эквипотенциальных линий. График потенци­ала вне тела будет также симметричен относительно максимума, но макси­мум, относительно точки заряда, сместиться в сторону.

Иное распределение потенциала будет наблюдаться в присутствии другого проводящего тела, находящегося вблизи точки заряда. Подобная ситуация показана на рис.2. Проводящий сфероид в поле зарядного тела (сферы) приобретает собственный потенциал. Так как сфероид имеет бесконечно малое сопротивление, то на всей его поверхности потенциал будет одинаковый (отсутствуют потери). Вокруг сфероида в окружающем пространстве, за счет эмиссии зарядов, будет создано собственное электрическое поле.

 

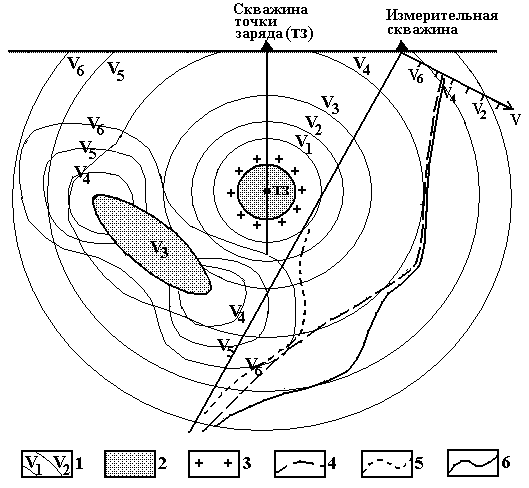
Рис.2. Распределение зарядов на поверхности проводящих объектов, эквипотенциальные линии вокруг этих объектов и графики потенциалов в окружающем пространстве для проводящего тела с точкой заряда (тз) и находящегося рядом другого проводящего тела. 1 – изолинии и значения потенциалов; 2 – проводящие тела; 3 – заряды на поверхности зарядного тела; 4 – график потенциалов в измерительной скважине от зарядного тела; 5 – то же от проводящего сфероида; 6 – суммарный наблюдаемый график потенциалов.

 

Если мы будем проводить измерение потенциала в скважине, проходя­щей вне проводящих тел, как показано на рис.2, то измеряемый потенциал будет суперпозицией потенциальных полей от двух тел. В результате на сум­ма­р­ном графике потенциалов мы получим два максимума и один минимум между ними.

Реальные объекты, в отличие выше рассмотренных модельных тел, имеют конечные значения сопротивления (проводимости), могут быть ани­зотропны и неоднородны. Если реальное тело находится в электрическом поле, то на его поверхности, в зависимости от его размеров и пространствен­ного положения относительно зарядного тела, возникнут различные потенци­алы (у модельного проводящего тела потенциалы на поверхности одинако­вы). Эта разность потенциалов приведет к образованию тока натекания по поверхности тела, что в свою очередь приведет к перераспределению зарядов на поверхности реального объекта. Величина тока натекания будет зависеть от градиента первичного поля, сопротивления и размеров реального объекта.

Ниже рассмотрим три варианта расположений точек ЗТ (заряда тела) или ЗП (зарядный пункт), ЗС (зарядной скважины) и ИС (измерительной скважины).

 

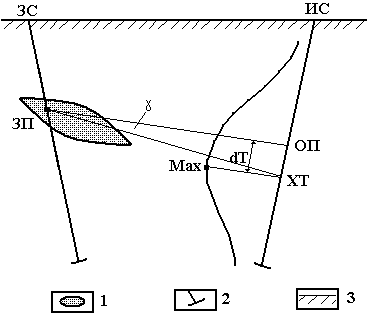
Рис.3. Рудное тело не дости­гает измерительной скважины. Усло­вные обозначе­ния: 1 – проводящее тело; 2- скважины; 3 – поверхность раздела земля-воздух.

 

 

Отрезок, направленный от точ­ки ЗПк XT и соединяющий их, на­зывается корреляционной осью. Корреляци­он­ная ось может зани­мать аномаль­ное положение, соответст­ву­ющее аномалии dХТ и ха­рактеризуе­мое угловой аномалией γ(Рис.3 ). Ее про­водят иногда и к точке минимума. Характерная точка ОП - основанием пер­пендикуляра, опущенного из точки ЗП (ЗТ)на ось ИС.

 

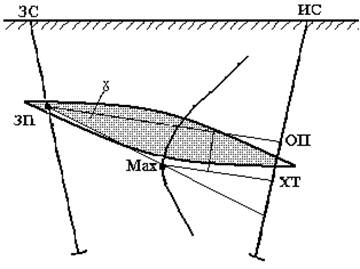
Рис.4. ЗП и ИС находятся в одном и том же рудном теле, то принци­пиа­льно кривая по­те­н­циала не изменит­ся (при условии сохра­нения формы и угла наклона руд­ного тела), но резко возрастет зна­чение потен­циала.

 

Таким образом, корреля­цион­ные кривые несут инфор­ма­­­цию о геоэлек­три­ческом стро­­ении околоскважинного, меж­скважинного, заскважин­ного, а также око­ловыработочного и межвыработочного пространства. Эта информа­ция извле­кается в процессе количест­венной и качественной интер­пре­тации, которая выполняется спе­циально разработанными способами.

Если же в меж­сква­жин­ной, засква­жинной или подза­бой­ной областях име­ются крупные геоэле­к­­три­чес­кие неодно­ро­д­ности, то кор­реля­ци­онные кривые претер­пят соответствующие изменения. В част­но­сти, на кривой по­тен­циала могут обра­зова­ться точки и зоны ми­нимума (ТМ), до­полнительные максимумы, и характерная точка (XT) может сместиться по отношению к точке ОП.

 

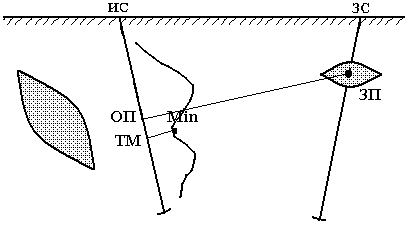Рис.5. Проводящее тело находится вне зарядной и измерительной скважин.

 

Перемещение заряда из точки ЗП1 в точку ЗП2 вызывает смену области эмиссии областью натекания тока, кото­рые фиксируются кривыми 1 и 2соответственно (рис.6.).

Рис.6. Проводящее тело находится вне зарядной и измерительных скважин. Условные обозначения: ρ₂ – удельное сопротивление рудного тела; ρ₁ - – удельное сопротивление вмещающих пород; ЗП1 и ЗП2 – зарядные точки 1 и 2; 1 и 2 – соотвествующие зарядным точкам 1 и 2 кривые потенциалов в измерительной скважине (ИС); δ – угол между верти­ка­лью и осью скважины; γ – угол между зарядным пунктом 1 (ЗП1) и перпендикуляром, опущенным из ЗП1 на ось измерительной скважины (ОП); Δ – расстояние между линией, соединяющей характерные точки ТМ и ХТ и перпендикуляром, опущенным на эту линию из точки ЗП1.

 

 

Метод электрической корреляции (МЭК) реализуется в трех вариантах - скважинном, поисково-картировочном (по­верхность - скважина) и шахтном (рис.4).

В скважинном варианте в зарядной скважине (ЗС) помещают питаю­щий электрод А, а по соседней измерительной скважине (ИС) снимают кор­реляционные кривые - кривую потенциала (рис. 4а) или реже его градиента при помощи соответственно зондов М и MN. В однородно-изотропной среде при пренебре­жимо малом влиянии границы земля — воздух точка макси­мума потенциала или точка перехода через нуль его градиента будет сов­падать с основанием перпендикуляра (ОП), опущенного из точки А на ось ИС. Если же в межскважинной, заскважинной или подзабойной областях имеются крупные геоэлектрические неодно­родности или среда анизотропна, то корреляционные кривые претерпят соответствующие изменения. В част­но­сти, на кривой по­тенциала могут образоваться точки и зоны минимума (ТМ), до­полнительные максимумы, и характерная точка (XT) может смести­ть­ся по отношению к точке ОП.

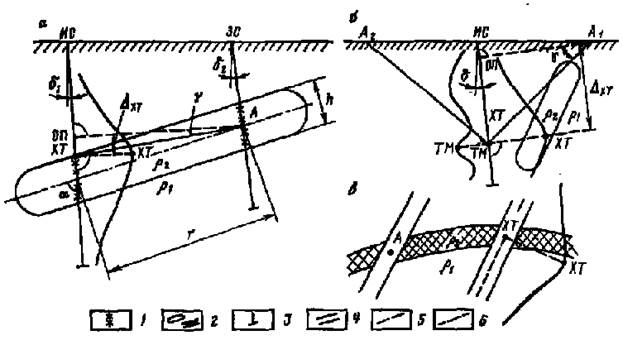
Рис.4. Основные варианты МЭК: а) – скважинный; б) – поисково-картировоч­ный; с) – шахтный; 1 – проводящие подсечения; 2 – проводящие объекты; 3 – скважины; 4 – горные выроботки; 5 – ось проводящего объекта; 6 – трассы наблюдений.

 

Аномалия положения характерной точки: Δ_ХТ = h_ХТ - h_ОП, где h_ХT и h_ОП

- глубины соответствующих точек.

Отрезок, направленный от точки А к XT и соединяющий их, называет­ся корреляционной осью. Корреляционная ось может зани­мать аномальное положение, соответствующее аномалии Δ_ХТ и ха­рактеризуемое угловой ано­малией γ (рис.4а, б). Ее про­водят иногда и к точке минимума.

При поисково-картировочном варианте МЭК электрод А последова­те­ль­но заземляется в точках земной поверхности по системе профилей или чаще радиальных лучей, проходящих через устье ИС; по измерительной скважине снимают кривые потенциала. Корреляционные кривые для однородно-изотропного полупрост­ранства будут иметь нормальный вид. Если же в околоскважинном или подзабойном пространстве находятся неоднородности или нижнее полупространство анизотропно, то на коре­ля­ционных кривых могут образоваться точки минимума, аномалии положения XT и корреляционных осей, угловые аномалии (рис. 4б). Таким образом, корреляционные кривые несут информацию о геоэлектрическом строении околоскважинного, межскважинного, заскважинного, а также околовы­рабо­точ­ного и межвыработочного пространства. Эта информация извлекается в процессе количест­венной и качественной интерпретации, которая выполняя­ется спе­циально разработанными способами.

Корреляционные кривые формируются под действием трех ос­новных факторов — эмиссии, натекания тока и экранирования поля. В области эми­ссии корреляционные кривые имеют характер­ную точку. Область натекания отмечается точкой или зоной мини­мума, окаймленной двумя максимумами, соответствующей незаря­женному проводнику. Перемещение заряда из точки А1, в точку А2 вызывает смену области эмиссии областью натекания тока, кото­рые фиксируются кривыми 1 и 2 соответственно (рис. 4б).

Экранирование прежде всего проявляется при разобщении об­ластей на­блю­дения поля и замещении его источника проводником или, напротив, высо­коомным объектом. Вследствие натекания тока на достаточно протя­же­нный проводник, по одну сторону которого расположен источник поля А и основание перпендикуляра, харак­терная точка корреляционной кривой смещается с ОП по направ­лению от проводника. В аналогичной ситуации изолятор смещает XT кривой в свою сторону. Типичный и важный пример проявле­ния этих разновидностей натекания и экранирования - влияние на положение XT корреляционных кривых покровных низкоомных отложений и соответственно - границы раздела земля - воздух.

Основной объект исследования в МЭК — проводники. При увязке под­сечений двух соседних скважин хорошим проводником следует считать такой, для которого XT корреляционной кривой еще лежит на его контакте при данных значениях расстояния R между ЗС и ИС по оси проводника, его мощности h, угла встречи α и параметра μ = ρ2/ρ1, где ρ2 и ρ1 – соответствен­но значения УЭС изучаемого проводящего тела и вмещающей среды. Такая ситуа­ция показана на рис.4а, где угол встречи α равен предельному минима­льному углу α_ПРmin. Если α<α_ПPmin, то XT кривой распо­лагается вне тела.

Объектом корреляции могут быть и анизотропные образования – Ани­зо­тропный пласт, залегаю­щий среди изотропных пород, или же изотропный пласт, залегаю­щий среди пород анизотропных.

В ряде случаев, например, когда проводники, пересеченные со­седними скважинами, не идентифицируются, возникает задача оп­ределения длины вы­клинивающейся в межскважинной области части заряженного проводящего тела. Решение этой задачи, а также определение контура рудного тела в пло­скости профиля бурения и оценка размеров рудных тел разработаны, за неболь­шими исключениями, для идеально проводящих объектов. С уче­том этого обстоятельства применительно к данным задачам и оп­ределяется поня­тие достаточно хорошего проводника. Хотя при этом предельная величина и находится в некоторой зависимости от геометрических факторов, расчеты и опыт позволяют использо­вать для оценок значение μ<0,01. Такие рудные проводники пред­ставляют и наибольший практический интерес.

Количественная интерпретация результатов измерений в МЭК осуще­ствляется при помощи палеток, номограмм и путем расчетов по соответ­ст­вую­щим формулам.

Для записи корреляционных кривых по скважинам, как пра­вило, испо­ль­зуют каротажные станции. Если возникает необходимость в применении больших токов пита­ния, превышающих максимально допустимые для каро­тажных станций, а также если непрерывная запись кривых становится не­возможной или ненужной, прибегают к поточечным измерениям с шагом в 2—10 м или же к одиночным замерам. Иногда, например при опоисковании межскважинного пространства в сравнительно низкоомных сре­дах и при больших расстояниях между ЗС и ИС, целесообразно применять электрораз­ведочные станции.

Метод электрической корреляции используют в скважинах на­земного и подземного бурения, а также в горных выработках на всех стадиях поиско­во-разведочных работ, начиная с поисковых работ и кончая эксплуатации­онной разведкой. Работы ведутся на медноколчеданные, полиметаллические, магнетитовые и другие хо­рошо проводящие руды. Метод может быть испо­ль­зован при гид­рогеологических изысканиях (корреляция трещиноватых зон, изу­чение подземных пресноводных потоков). В ряде случаев МЭК дает хоро­шие результаты при решении структурно-геологических задач. При этом изу­чаемые объекты — обводненные и, следова­тельно, низкоомные или, напро­тив, «залеченные» высокоомные зоны тектонических нарушений.

Полноценное использование возможностей МЭК требует предварите­ль­ного проведения работ по ГИС, в которые обязательно должны входить метод сопротивлений и инклинометрия. Являясь составной частью комп­лекса поисково-разведочных работ, МЭК обеспечивает полноту и завершен­ность коррелирования разрезов скважин.

Скважинным вариантом МЭК решаются следующие задачи.

1. Увязка проводящих или анизотропных подсечений, которая проводится на основании сопоставления положения точек XT, ОП и ТМ, подсечений, точек заряда, осей зарядных и измерительных скважин. Положение XT корреляционной кривой на изучаемом подсечений — обязательный признак увязки. При необходимости используют экранные явления. При интерпретации учитывают осо­бенности формы кривых и геоэлектричес­кого разреза, геологиче­ские условия. Круг неоднозначности интерпрета­ции сужается за счет рассмотрения всей совокупности корреляционных кривых по данному узлу скважин.

2. Определение положения высокоомных образований в межскважинном пространстве с использованием экранных явлений. Возможно также применение МЭК ПВС — метода электрической корреляции пластов высокого сопротивления.

3. Определение длины выклинивающейся в межскважинном пространстве части рудного.

4. Определение направления и угла падения. Направление па­дения опреде­ляется по положению корреляционных осей. Кажущийся и истинный углы падения находят различными путями в зависимости от ситуации. Оценка размеров рудных тел.

5. Обнаружение рудных тел в межскважинном и подзабойном пространстве. В межскважинном пространстве проводники выяв­ляются прежде всего по положению (схождению) корреляционных осей. Большое значение имеют точки минимума.

6. Оценка анизотропии однородных горных пород.

Поисково-картировочным вариантом МЭК ре­шаются задачи:

1. Увязка рудных тел, вскрытых карьерами, шурфами и кана­вами, с рудными подсечениями в скважинах.

2. Выявление проводников в подзабойном и околоскважинном пространстве с использованием особенностей кривых в зонах натекания и эмиссии тока, а также аномалий в положении корреля­ционных осей.

3. Картирование проводящих или анизотропных горных пород под покров­ны­ми отложениями по изменению типа корреляцион­ных кривых при пере­мещении электрода А.

4. Определение направления падения горных пород по поло­жению кор­ре­ляционных осей.

5. Определение коэффициента анизотропии мощных однород­ных толщ горных пород путем расчета по соответствующим фор­мулам.

В табл.1 приведены результаты оценки размеров рудных тел медноколче­дан­ного месторождения по палеткам. Оценка размеров выполнялась по отдельным скважинам.

 

 

Таблица 1.

Оценка размеров рудных тел на медноколчеданном месторождении

Индекс тела	Длина тела, м	Погреш­- ность, %	Ширина тела, м	Погреш­- ность, %
Бурение	Геофизика	Бурение	Геофизика
А Б В Г			+ 34 - 26 + 20 + 4	40 - 120		- 38 - 36 - 47 + 50

 

 

Поделиться:

Воспользуйтесь поиском по сайту: