Научно-педагогическая деятельность

Мещерский, Иван Всеволодович

Ива́н Все́володович Меще́рский (29 июля (10 августа) 1859, Архангельск — 7 января) 1935, Ленинград) — русский и советский учёный-механик, основоположник механики систем переменного состава^[1] (систем переменной массы).

Биография

Родился в городе Архангельске в небогатой семье. В 1878 г. поступил на математическое отделение физико-математического факультета Петербургского университета. Это было время расцвета Петербургской математической школы, созданной П. Л. Чебышёвым. Здесь Мещерский с интересом слушал лекции как самого Чебышёва, так и известных в то время профессоров А. Н. Коркина (1837—1908), К. А. Поссе (1847—1928) и многих других.

В студенческие годы Мещерский с особым интересом занимался механикой. В 1882 г. он окончил университет и был оставлен для подготовки к профессорскому званию. С этого времени начинается его более чем полувековая научно-педагогическая деятельность. В 1891 г. он получил кафедру механики на Петербургскихвысших женских курсах, которую занимал до 1919 г., то есть до слияния этих курсов с университетом. В 1897 г. Мещерский успешно защитил в Петербургском университете диссертацию на тему «Динамика точки переменной массы», представленную им для получения степени магистра прикладной математики.

В 1902 г. он был приглашён заведовать кафедрой в Петербургский политехнический институт. Здесь до конца жизни протекала его основная научно-педагогическая работа. И. В. Мещерский 25 лет вёл педагогическую работу в Петербургском университете и 33 года — в Политехническом институте. За эти годы он обучил тысячи специалистов. Многие его слушатели стали крупными учёными (академик А. Н. Крылов, профессорГ. В. Колосов и др.).

За выдающиеся заслуги в области науки И. В. Мещерскому в 1928 году было присвоено звание заслуженного деятеля науки. Его именем назван кратер Мещерский (англ. Meshcherskiy) на Луне.

 

Научно-педагогическая деятельность

Широко известен курс теоретической механики И. В. Мещерского и особенно его «Сборник задач по теоретической механике» (первое издание — 1914 г.), выдержавший (на конец 2012 г.) 51 издание и принятый в качестве учебного пособия для высших учебных заведений не только в СССР, но и в ряде зарубежных стран. Сборник Мещерского, как и его работа «Преподавание механики и механические коллекции в некоторых высших учебных заведениях Италии, Франции, Швейцарии и Германии» (1895), немало способствовали подъёму научного и педагогического уровня преподавания механики в высших учебных заведениях России.

И. В. Мещерскому принадлежит ряд работ по общей механике, но наибольшую известность получили его исследования по динамике точки переменной массы. Уже упоминавшаяся его работа «Динамика точки переменной массы» (1897) стала основополагающей в процессе становления механики систем переменной массы (или систем переменного состава — более точный термин, предпочитаемый авторами современных изданий^[2][3][4]). Во втором выдающемся труде Мещерского «Уравнения движения точки переменной массы в общем случае» (1904) его теория получила окончательное и в высшей степени изящное выражение. Здесь он устанавливает и исследует общее уравнение движения точки, масса которой изменяется от одновременного процесса присоединения и отделения материальных частиц (ныне это уравнение известно как уравнение Мещерского).

И. В. Мещерский не только разработал теоретические основы динамики точки переменной массы, но и рассмотрел большое количество частных задач о движении таких точек (например, задачи о восходящем движении ракеты и вертикальном движении аэростата). Он подверг весьма обстоятельному исследованию движение точки переменной массы под действием центральной силы, заложив тем самым основания небесной механики тел переменной массы. Он исследовал также и некоторые проблемы движения комет. И. В. Мещерский впервые сформулировал и так называемые обратные задачи динамики точки переменной массы, когда по заданным внешним силам и траекториям определяется закон изменения массы.

Огромное практическое значение исследований И. В. Мещерского в области механики точки переменной массы выявилось с достаточной полнотой лишь после окончания Второй мировой войны, когда человечество вплотную подошло (а затем и приступило) к освоению космического пространства. В это время появляется большое число глубоких теоретических исследований, посвящённых как специальным проблемам ракетодинамики и динамики тел переменного состава, так и значительному обобщению результатов исследований Мещерского. Опираясь на его труды, многие советские и зарубежные учёные разработали основные вопросы динамики произвольных изменяемых систем переменного состава. Технический прогресс в области реактивного движения наглядно показывает проницательность и глубину научных исканий Мещерского.

В историю науки Мещерский вошёл как основоположник механики систем переменного состава (переменной массы). Его исследования в этой области явились теоретической основой современной ракетодинамики. Его имя неразрывно связано с именем одного из создателей научных основ космонавтики — К. Э. Циолковского.

Научные труды

· 1887 год — «Дифференциальные связи в случае одной материальной точки^[5].», Харьков, Университетская типография, 12 страниц.

· 1897 год — «Динамика точки переменной массы.», Магистерская диссертация, Санкт-Петербургский Университет.

· 1897 год — «Динамика точки переменной массы, рассуждения.», Санкт-Петербург, Типография Императорской Академии Наук, 160 страниц.

· 1904 год — «Уравнение движения точки переменной массы в общем случае.», Известия Санкт-Петербургского Политехнического Университета, часть 2, страницы 77-118.

· 1907 год — «Теоретическая механика.», лекции, читаемые профессором И. В. Мещерским в Санкт-Петербургском Политехническом Институте в 1906—1907 учебных годах, в 2-х частях, Санкт-Петербург: Издательство студенческой кассы взаимопомощи при Санкт-Петербургском Политехническом Институте, 316 страниц.

· 1909 год — «Сборник задач, относящихся к курсу Теоретическая механики.», часть 1-я, Санкт-Петербург: Издательство студенческой кассы взаимопомощи при Санкт-Петербургском Политехническом Институте, 91 страница (переиздан в 1998 году, 37-е издание, 448 страниц).

· 1911 год — «Кабинет теоретической механики Санкт-Петербургского Политехнического Института Императора Петра Великого.», Санкт-Петербург, 8 страниц.

· 1918 год — «Задача из динамики переменных масс.», Известия Первого Петроградского Политехнического Института, том 27, страницы 101—112.

· 1918 год — «Гидродинамическая аналогия прокатки.», Известия Первого Петроградского Политехнического Института, том 27, страницы 141—179.

· 1921 год — «Дифференциальные уравнения движения гироскопического вагона однорельсовой железной дороги.», Петроград, страницы 133—162.

Награды

Действительный статский советник И. В. Мещерский был награждён Правительственными наградами Российской Империи:

· 1915 год — «Заслуженный профессор Петроградского Политехнического Института Императора Петра Великого» (это почётное звание И. В. Мещерскому было присвоено за заслуги в области научной и педагогической деятельности).

· 1928 год — «Заслуженный деятель науки РСФСР» (это почётное звание И. В. Мещерскому было присвоено по ходатайству Совета ПетроградскогоПолитехнического Института за выдающиеся заслуги в области науки).

За выслугу лет и безупречную службу он был пожалован орденами и медалями:

· 1898 год — Орден Святого Станислава, 3-ей степени;

· 1902 год — Орден Святой Анны, 3-й степени;

· 1906 год — Орден Святой Анны, 2-й степени;

· 1916 год — Орден Святого Владимира, 4-й степени;

Серебряные медали в память Царственного Императора Александра III 2-й, 3-й и 4-й степеней.

 

Источники:

1. ↑ Под словом «состав» понимают совокупность частиц, образующих механическую систему в каждый конкретный момент времени (иными словами, термин «система переменного состава» используется не в том смысле, какой в него вкладывается в химии и статистической физике).

2. ↑ Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3. — С. 214.

3. ↑ Голубев Ю. Ф. Основы теоретической механики. 2-е изд. — М.: Изд-во Моск. ун-та, 2000. — 720 с. — ISBN 5-211-04244-1. — С. 404.

4. ↑ Веретенников В. Г., Синицын В. А. Теоретическая механика (дополнения к общим разделам). 2-е изд. — М.: Физматлит, 2006. — 416 с. — ISBN 5-9221-0703-8. — С. 71.

5. ↑ ИСТОРИКО-ТЕХНИЧЕСКИЙ МУЗЕЙ Санкт-Петербурского государственного политехнического университета

Мещерский Иван Всеволодович // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.

 

 

Уравнение Мещерского

История открытия

Уравнение движения материальной точки переменной массы для случая присоединения (или отделения) частиц было получено и основательно исследовано в магистерской диссертации И. В. Мещерского, защищенной в Петербургском Университете 10 декабря 1897 года^[9]. Первое сообщение об уравнении движения материальной точки переменной массы в общем случае одновременного присоединения и отделения частиц было сделано И. В. Мещерским 24 августа 1898 года на заседании секции математики и астрономии X съезда русских естествоиспытателей и врачей в Киеве, широкую известность оно получило позднее, после работы «Уравнения движения точки переменной массы в общем случае», напечатанной в «Известиях Петербургского политехнического института» в 1904 году^[10].

Следует отметить, что по исследованиям Г. К. Михайлова, изложенным в его докторской диссертации^[11] и работе «Георг Бюкуа и начала динамики систем с переменными массами»^[12], аналогичное уравнение было установлено чешским учёным-любителем Георгом Бюкуа (1781—1851) ещё в работах 1812—1814 гг.

Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное И. В. Мещерским в 1897 году^[1] для материальной точки переменной массы (состава).

Уравнение обычно записывается в следующем виде:

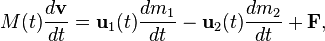
где:

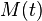· — масса материальной точки, изменяющаяся за счет обмена частицами с окружающей средой, в произвольный момент времени t;

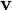· — скорость движения материальной точки переменной массы;

· — результирующая внешних сил, действующих на материальную точку переменной массы со стороны её внешнего окружения (в том числе, если такое имеет место, и со стороны среды, с которой она обменивается частицами, например электромагнитные силы — в случае массообмена с магнитной средой, сопротивление среды движению и т. п.);

· — относительная скорость присоединяющихся частиц;

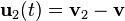· — относительная скорость отделяющихся частиц;

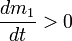· и 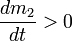— скорость увеличения суммарной массы присоединившихся частиц и скорость увеличения суммарной массы отделившихся частиц соответственно.

Формула Циолковского может быть получена как результат решения этого уравнения.

Величина:

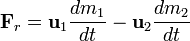
называется «реактивной силой».

Вывод уравнения Мещерского из второго закона Ньютона в форме

где масса материальной точки считается непостоянной, приведён в книге^[2].

Обычно^[3][4][5] уравнение Мещерского получают, основываясь на уравнении для скорости изменения импульса системы материальных точек, имеющим вид:

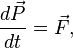
где 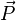— импульс системы, равный сумме импульсов всех материальных точек, составляющих систему, а — равнодействующая всех внешних сил, действующих на тела системы. Ниже приведён вывод уравнения, использующий именно такой подход.

Вывод Уравнения Мещерского

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: