 |
Задание 6. Выявление различий в уровне исследуемого признака.
|
|
|
|
Варианты заданий для контрольной работы
По дисциплине «Прикладная математика»
Задание 1. Выборка, её числовые характеристики
Для указанных ниже статистических распределений выборок требуется:
1) Найти эмпирическую функцию распределения и построить ее график.
2) Построить полигон частот.
3) Вычислить выборочную среднюю.
4) Вычислить выборочную и исправленную дисперсии.
Вариант 1. xi 1 4 8 10
ni 5 3 2 1
Вариант 2. xi-5 1 3 5
ni 2 5 3 1
Вариант 3. xi 1 5 9 11
ni 2 3 5 1
Вариант 4. xi -2 1 2 3 4 5
ni 2 1 2 2 2 1
Вариант 5. xi0 1 2 3 4
ni5 2 1 1 1
Вариант6. xi1 5 6 8
ni5 15 20 10
Вариант 7. xi1 5 7 9
ni6 12 1 1
Вариант 8. xi 2 3 5 6
ni 10 15 5 20
Вариант 9. xi-5 2 3 4
ni 4 3 1 2
Вариант 10. xi 1 2 4 7
ni 1 3 6 2
Задание 2. Линейная корреляция
По данным, приведенным ниже, вычислить коэффициент корреляции, найти выборочное уравнение прямой линии регрессии Y на X, построить корреляционное поле и нанести на него прямую регрессии Y на X.
Вариант 1. X 
5 9 10 12
Y 3 6 4 7
Вариант 2. X 1 2 5 8 16
Y 1,0 1,4 2,2 2,8 4,0
Вариант 3. X 1 3 4 7 10
Y -1,0 -2,1 -2,4 -3,0 -3,3
Вариант 4. X 2 5 7 10
Y 2 4 6 8
Вариант 5. X -1 -0,5 0 0,8 1,5
Y 2,7 3,2 4,0 6,5 11,0
Вариант 6. X -2 -1 0 1 2
Y 15,8 6,4 3,0 1,7 1,3
Вариант 7. X 1 3 6 8 10
Y 8,9 5,6 3,5 2,7 2,0
Вариант 8. X 1 3 6 10
Y 5,5 6,9 7,4 7,5
Вариант 9. X 9,5 10,5 11,0 12,0 14,5
Y 4,5 6,0 8,5 9,0 10,0
Вариант 10. X 6,6 7,0 8 9 9,8
Y 6,0 7,8 8,7 7,8 9
Задание 3. Статистическая проверка статистических гипотез
В вариантах 1–10 приведено эмпирическое распределение дискретной случайной величины X. Требуется, используя критерий 
, проверить на уровне значимости 
=0,05 гипотезу о распределении генеральной совокупности по закону Пуассона.
1. Случайная величина X – число вышедших из строя станков в цехе за одну смену. Число наблюдений n = 200:
|
|
|
xi 0 1 2 3 4 5 6 7 
8
ni 41 62 45 22 16 8 4 2 0
2. Случайная величина X – число нестандартных коробок консервов в одном ящике. Число наблюдений n = 200:
xi 0 1 2 3 4 5
ni 132 43 20 3 2 0
3. Случайная величина X – число отказов радиоэлектронной аппаратуры. Число наблюдений n = 60:
xi 0 1 2 3 4
ni 42 11 4 3 0
4. Случайная величина X – число неправильных соединений в минуту на телефонной станции. Число наблюдений n = 60:
xi 0 1 2 3 4 5 6 7 8
ni 8 17 16 10 6 2 0 1 0
5. Случайная величина X – число деталей, поступивших на конвейер в течение 2-х минутного интервала. Число наблюдений n = 600:
xi 0 1 2 3 4 5 6 7
ni 400 167 29 3 0 0 1 0
6. Случайная величина X – число поврежденных стеклянных изделий в контейнере. Число наблюдений n = 500:
xi 0 1 2 3 4 5 6 7 8
ni 199 169 87 31 9 3 1 1 0
7. Cлучайная величина X – число сбоев в работе ЭВМ за неделю. Число наблюдений n = 20:
xi 0 1 2 3 4 5
ni 109 65 22 3 1 0
8. Случайная величина X – число заявок, поступающих на телефонную станцию в минуту. Число наблюдений n = 100:
xi 0 1 2 3 4 5 6 7 8
ni 7 21 26 21 13 7 3 2 0
9. Случайная величина X – число неправильно сброшюрованных учебников в партии. Число наблюдений n = 1000:
xi 0 1 2 3 4 5 6
ni 505 336 125 24 8 2 0
10. Случайная величина X – число заявок, поступающих в систему массового обслуживания в течение часа. Число наблюдений n = 100:
xi 0 1 2 3 4 5 6 7 8 9 10 11
ni 1 3 8 14 17 17 15 10 7 5 2 1
Задание 4. Доверительные интервалы для параметров нормального закона распределения
Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 
= 0,95, зная выборочную среднюю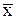 
, объем выборки n и среднее квадратичное отклонение 
Вариант 1. 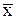= 75,17; n = 36; 
Вариант 2. 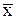= 75,16; n = 49; 
Вариант 3. 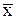= 75,15; n = 64; 
Вариант 4. 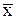= 75,14; n = 81; 
Вариант 5. 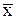= 75,13; n = 100; 
Вариант 6. 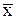= 75,12; n = 121;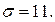 
Вариант 7. 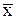= 75,11; n = 144;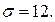 
Вариант 8. 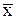= 75,10; n = 169; 
Вариант 9. 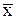= 75,09; n = 196; 
Вариант 10. 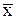= 75,08; n = 225; 
Задание 5.
В группе n студентов. По контрольной работе n1 студентов получили 5 баллов, n2 студентов получили 4 балла, n3 студентов получили 3 балла и n4 студента получили 2 балла. Можно ли считать, что мы имеем дело с группой «троечников»?
|
|
|
1.1 n = 30, n1 = 5, n2 = 6, n3 = 12, n4 = 7.
1.2 n = 32, n1 = 6, n2 = 7, n3 = 13, n4 = 6.
1.3 n = 28, n1 = 5, n2 = 5, n3 = 10, n4 = 8.
1.4 n = 30, n1 = 6, n2 = 5, n3 = 11, n4 = 8.
1.5 n = 24, n1 = 4, n2 = 6, n3 = 9, n4 = 5.
1.6 n = 28, n1 = 6, n2 = 6, n3 = 12, n4 = 4.
1.7 n = 32, n1 = 5, n2 = 7, n3 = 14, n4 = 6.
1.8 n = 24, n1 = 5, n2 = 5, n3 = 10, n4 = 4.
1.9 n = 26, n1 = 6, n2 = 5, n3 = 9, n4 = 6.
1.10 n = 28, n1 = 4, n2 = 5, n3 = 13, n4 = 5.
Указание. Решить задачу с помощью критерия Пирсона.
Задание 6. Выявление различий в уровне исследуемого признака.
В таблице (ниже) представлены значения вербального интеллекта, полученные с помощью методики Векслера у студентов-физиков (А), студентов-психологов (В), студентов-биологов (С), студентов-экологов (D) и студентов-историков (Е) университета. Требуется установить:
2.1. Превосходят ли студенты-физики (А) студентов-психологов (В) по уровню вербального интеллекта?
2.2. Превосходят ли студенты-физики (А) студентов-биологов (С) по уровню вербального интеллекта?
2.3. Превосходят ли студенты-физики (А) студентов-экологов (D) по уровню вербального интеллекта?
2.4. Превосходят ли студенты-физики (А) студентов-историков (Е) по уровню вербального интеллекта?
2.5. Превосходят ли студенты- психологи (В) студентов-биологов (С) по уровню вербального интеллекта?
2.6. Превосходят ли студенты-психологи (В) студентов-экологов (D) по уровню вербального интеллекта?
2.7. Превосходят ли студенты-биологи (С) студентов-историков (Е) по уровню вербального интеллекта?
2.8. Превосходят ли студенты-психологи (В) студентов-историков (Е) по уровню вербального интеллекта?
2.9. Превосходят ли студенты- биологи (С) студентов-экологов (D) по уровню вербального интеллекта?
2.10. Превосходят ли студенты-экологи (D) студентов- историков (Е) по уровню вербального интеллекта?
Таблица 1.
| № п/п | А: физики | В: психологи | С: биологи | D: эко-логи | Е: историки |
Указание. Решить задачу с помощью критерия U Манна-Уитни, критические значениядля n1=n2=12:
U кр= 42 (
=0.05) и U кр = 31 ( =0.01).
|
|
|
