 |
Интегрирование дробно-рациональных функций.
|
|
|
|
Всякая рациональная функция  есть дробь
есть дробь  , где
, где  и
и 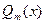 многочлены соответственно n-ой и m-ой степени.
многочлены соответственно n-ой и m-ой степени.
Если  - дробь правильная.
- дробь правильная.
Если  - дробь неправильная. В этом случаи при интегрировании дроби сначала следует выделить целую часть (разделить
- дробь неправильная. В этом случаи при интегрировании дроби сначала следует выделить целую часть (разделить  на
на 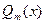 ), и тогда
), и тогда

 , где
, где  - многочлен, который легко интегрируется, а
- многочлен, который легко интегрируется, а  - правильная дробь.
- правильная дробь.
Пример:
1. 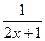 ,
,  - правильные дроби.
- правильные дроби.
2. 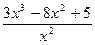 - неправильная дробь, для интегрирования ее следует записать в виде
- неправильная дробь, для интегрирования ее следует записать в виде  ;
;
3. 
 - неправильная дробь, для интегрирования ее следует записать в виде
- неправильная дробь, для интегрирования ее следует записать в виде  (разделите “уголком” числитель данной дроби на знаменатель).
(разделите “уголком” числитель данной дроби на знаменатель).
Задача интегрирования дробно-рациональной функции свелась к задаче интегрирования правильной дроби.
Раньше уже рассматривались некоторые частные случаи. Сделаем некоторые обобщения.
Интегралы вида  и
и 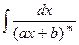 подстановкой
подстановкой  сводятся к табличным.
сводятся к табличным.
Интегралы вида  ,
,  ,
, 
 сводятся к табличному, выделив в знаменателе полный квадрат, подстановкой
сводятся к табличному, выделив в знаменателе полный квадрат, подстановкой  .
.
Для этого метода интегрирования понадобится еще известная теорема из алгебры.
Теорема. Если  правильная рациональная дробь, знаменатель которой
правильная рациональная дробь, знаменатель которой 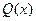 можно представить в виде произведения линейных и квадратичных множителей (с действительными коэффициентами), то эта дробь раскладывается на элементарные дроби:
можно представить в виде произведения линейных и квадратичных множителей (с действительными коэффициентами), то эта дробь раскладывается на элементарные дроби:
 , то
, то

+ 
+  .
.

Пример:
Дробь  - правильная.
- правильная.
Знаменатель  .
.
Тогда
 .
.
Коэффициенты A, B, C, D – пока неопределены. Большой любитель может их просто “подбирать”, но, понятно, в математике есть метод нахождения/вычисления этих коэффициентов. Он так и называется: метод неопределенных коэффициентов.
Сущность этого метода покажем на рассматриваемом примере.
В правой части равенства все три дроби приведем к общему знаменателю.
|
|
|
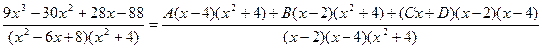 .
.
Констатируем: дроби равны; знаменатели этих дробей равны.
Значит, числители их тоже равны (в числителе правой дроби сделаны соответствующие тождественные алгебраические преобразования), т.е.

-  .
.
Многочлены в левой и правой частях равенства равны, следовательно равны коэффициенты при одинаковых степенях переменной х, т.е.

Решая полученную систему 4-х линейных алгебраических уравнений с 4-мя неизвестными A,B,C,D любым из известных многочисленных методов, получаем:  .
.
А значит,
 .
.
Интегрировать такую дробь уже легко:

= 
 =
=  .
.
Метод интегрирования также называется методом неопределенных коэффициентов.
Если интегрируется неправильная дробь, то, представив ее в виде суммы целой части (многочлена) и правильной дроби, процесс становится очевидным.
 |
Пример:
1.  .
.
 2.
2.  .
.
Интегрирование тригонометрических функций.
В этом параграфе будем говорить об интегрировании функций, рационально определяющихся через тригонометрические функции sinx, cosx. Их принято записывать в виде  .
.
Теорема. Интеграл

подстановкой  преобразуется в интеграл от рациональной функции (рационализируется).
преобразуется в интеграл от рациональной функции (рационализируется).
Доказательство этой теоремы основывается на известных формулах
 , т.е.,
, т.е.,  ;
;
 , т.е.,
, т.е.,  ;
;
а из равенства 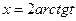 получаем
получаем  .
.
И  , т.е. интегрирование свелось к предыдущему методу.
, т.е. интегрирование свелось к предыдущему методу.
Подстановка  называется универсальной. Но не следует ею пользоваться во всех случаях, хотя она сработает во всех. Например, такие интегралы, как
называется универсальной. Но не следует ею пользоваться во всех случаях, хотя она сработает во всех. Например, такие интегралы, как  ,
,  ,
,  ,
,  и т.п., разумнее брать непосредственно.
и т.п., разумнее брать непосредственно.
 Пример:
Пример:

 .
.
Практикум по разделу 5.2.
Задание 1. Пользуясь  найти следующие неопределенные интегралы:
найти следующие неопределенные интегралы:
а)  ; а)
; а)  ; в)
; в) 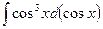 ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Задание 2. Проинтегрировать методом подстановки:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 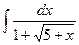 ; е)
; е)  ;
;
ж) 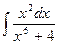 ; з)
; з)  ; и)
; и)  ;
;
к)  ; л)
; л)  ; м)
; м)  ;
;
н)  ; о)
; о)  ; п)
; п)  .
.
|
|
|
Задание 3. Проинтегрировать методом интегрирования по частям:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ; и)
; и)  ;
;
к)  ; л)
; л)  ; м)
; м)  ;
;
н) 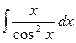 ; о)
; о)  .
.
Задание 4. Проинтегрировать дробно-рациональные функции:
а) 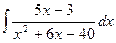 ; б)
; б)  ; в)
; в)  ;
;
г) 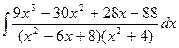 ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ; и)
; и)  ;
;
к)  ; л)
; л)  ; м)
; м)  ;
;
н)  ; о)
; о)  .
.
Задание 5. Проинтегрировать тригонометрические функции:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 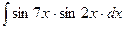 ; е)
; е)  ;
;
ж)  ; з)
; з)  ; и)
; и)  ;
;
к)  ; л)
; л) 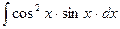 ;
;
м)  ; н)
; н) 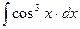 ; о)
; о) 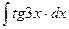 .
.
Задание 6. Проинтегрировать:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 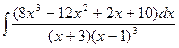 ;
;
е)  ;
;  ;
;
ж)  ; з)
; з)  ; и)
; и) 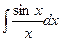 ;
;
к)  ; л)
; л)  ; м)
; м)  ;
;
н)  ; о)
; о)  ; п)
; п) 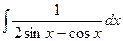 ;
;
р)  ; с)
; с)  ; т)
; т)  ;
;
у)  .
.
*) Знак - стилизованная буква S, часто используемая для обозначения суммы.
*) Наизусть! Это легко, если были выучены наизусть табличные производные
|
|
|


