 |
Построение модели линейной корреляции по несгруппированным данным
|
|
|
|
Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной.
Пусть опытные данные представлены в виде таблицы:
Таблица 1.7
| X | 
| 
| 
| 
| … | 
|
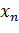
| Y | 
| 
| 
| 
| … | 
|
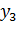
n – количество наблюдений за параметрами X и Y.
Данные не сгруппированы в корреляционную таблицу.
Изучение корреляционной связи будем проводить при решении двух основных задач:
- определение формы корреляционной связи, то есть вида теоретической функции регрессии (она может быть линейной и нелинейной);
- определение тесноты (силы) корреляционной связи и степени воздействия факторного признака X на результативный признак Y.
Наиболее простой и важный случай корреляционной зависимости - линейная регрессия. Предположим, что между двумя признаками существует линейная корреляционная зависимость, уравнение регрессии которой имеет вид:
| (1.19) |
Параметр b характеризует усредненное влияние на результативный признак Y неучтенных факторных признаков Xi. Параметр a называется коэффициентом регрессии и показывает, на сколько изменяется в среднем значение результативного признака Y при увеличении факторного признака X на единицу.
Для нахождения параметров линейной корреляции находят по методу наименьших квадратов. Преобразуем систему (1.17) следующим образом:
Введем обозначения
В результате, применяя к новой системе метод Кремера, получим:
(1.20)
Определение коэффициента эластичности.
На сколько изменяется в среднем значение результативного признака Y при увеличении факторного признака X на 1% показывает коэффициент эластичности Кэ:
|
|
|
| (1.21) |
Определение тесноты связи (коэффициент корреляции).
Для определения тесноты связи между признаками X и 
служит коэффициент корреляции r.
Для нахождения коэффициента корреляции определяют:
· среднее значение фактора X, результативного признака Y и среднее произведение значение признаков X и 
:
| 
| 
| (1.22) |
· среднее квадратическое отклонение фактора X и результативного признака Y:
| 
| (1.23) |
· коэффициент корреляции будет равен:
| (1.24) |
Свойства выборочного коэффициента корреляции:
1. 
.
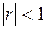2. Если 
, тогда признаки 
и 
не связаны линейной корреляционной зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
3. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при 
переходит в линейную функциональную зависимость.
4. Если 
, тогда признаки и связаны прямой (обратной) линейной функциональной зависимостью.
Оценку тесноты линейной корреляции определяют по шкале Чеддока (табл. 1.9).
Таблица 1.9
| Теснота связи | Значение коэффициента корреляции | |
| Линейной связи нет, переменные независимы |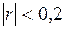 
| |
| Линейная связь слабая | 
| |
| Линейная связь средняя | 
| |
| Линейная связь сильная | 
| |
| Функциональная | 
| |
Определение доверительного интервала коэффициента корреляции.
Для определения коэффициента корреляции генерального совокупности 
определяют доверительный интервал. Для этого вычисляют значение средней квадратической ошибки 
по формуле:
| (1.25) |
В случае, если число наблюдений n <50, то доверительный интервал запишется в виде:
| (1.26) |
где 
это значение аргумента функции Лапласа 
(приложение 1), при котором 
. Для 
значение 
.
В случае, если число наблюдений n >50, то доверительный интервал находят по формуле:
|
|
|
| (1.27) |
Определение значимости выборочного коэффициента корреляции.
Значимость выборочного коэффициента корреляции проверяют по критерию Стьюдента 
:
| (1.28) |
По таблице критических точек распределения Стьюдента (Приложение 1) по заданному уровню значимости 
и числу степеней свободы 
находят критическое значение параметра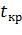 
.
Если 
, то коэффициент корреляции 
незначимый и признаки и 
некоррелированы. Если 
, то коэффициент корреляции значимый и признаки и связаны линейной корреляционной зависимостью.
Определение степени воздействия факторного признака X на результативный признак Y.
Степень воздействия факторного признака X на результативный признак Y показывает коэффициент детерминации:
| (1.29) |
где — опытные значения признака Y,
— значения y, найденные по уравнению регрессии,
— среднее значение признака Y.
Чем ближе значение 
к единице, тем лучше модель согласуется с опытными данными.
Проверка адекватности модели.
Чтобы установить, соответствует ли построенное уравнение регрессии опытным данным и достаточно ли включенных в уравнение факторных признаков X i для описания результативного признака необходимо проверить адекватность модели.
Для проверки соответствия уравнения регрессии опытным данным применяют критерий Фишера-Снедокора. Вычисляют 
:
| (1.30) |
По таблице критических точек распределения Фишера-Снедокора (Приложение 7) по заданному уровню значимости и числу степеней свободы 
находят критическое значение параметра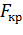 
.
Если 
, то уравнение регрессии согласуется с опытными данными. Если 
, то полученная модель регрессии не согласуется с опытными данными.
ПРИЛОЖЕНИЕ
Распределение Стьюдента - таблица значений
| п | g | п | g | ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 | 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 | 8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 | 20 25 30 35 40 45 50 60 70 80 90 100 120 ∞ | 2,093 2,064 2.045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960 | 2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576 | 3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291 |
|
|
|
|
|
|
