Рассмотрим алгоритмы перехода от одной формы к другой.

Введение.

Математическое программирование – раздел высшей математики, разрабатывающий теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Для решения экономической задачи математическими методами составляют математическую модель задачи, т.е. записывают ее с помощью математических выражений: неравенств, уравнений и т.п. Для математического описания экономической задачи можно руководствоваться следующей общей схемой:

1) выбирают некоторое количество переменных x₁,…..x_n, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого экономического процесса;

2) выражают взаимосвязи исследуемого экономического процесса в виде математических соотношений (уравнений, неравенств). Эти соотношения образуют систему ограничений математической модели;

3) поиск наилучшего решения формулируют в терминах поиска оптимального (максимального или минимального) значения функции

Z (x₁, ……x_n). Построенная функция называется целевой и обычно обозначается за Z=Z(x) или f=f(x).

Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений

Если Z (x₁, ……x_n) – линейная функция и линейны функции, описывающие ограничения на переменные x₁, ……x_n, то математическая модель представляет задачу линейного программирования (программирование употребляется в смысле планирования ).

Если хотя бы одна из указанных функций нелинейная, то математическая модель является объектом исследования нелинейного программирования.

1. Линейное программирование

Различные формы записи задачи линейного программирования.

Рассмотрим задачу линейного программирования (ЗЛП) в общем виде:

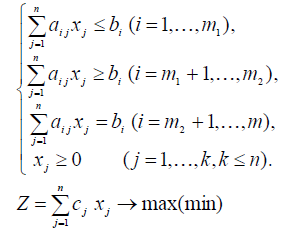
Линейное программирование – это раздел математического программирования, применяемый при отыскании экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные.

Задача линейного программирования задана в канонической форме, если требуется максимизировать целевую функцию, а все ограничения системы – уравнения и на все переменные наложено условие неотрицательности.

Задача линейного программирования задана в симметричной форме, если требуется максимизировать целевую функцию, все ограничения системы – неравенства «≤»(или минимизировать целевую функцию, все ограничения системы – неравенства «≥») и на все переменные наложено условие неотрицательности.

Набор чисел Х=(x₁, ……,x_n) называется допустимым решением (планом), если он удовлетворяет системе ограничений ЗЛП.

Множество всех допустимых решений называется областью допустимых решений (ОДР).

Допустимое решение X^*=(, ……, ), для которого достигается максимальное (минимальное) значение функции, называется оптимальным планом ЗЛП.

Все формы записи ЗЛП являются эквивалентными в том смысле, что имеются алгоритмы перехода от одной формы к другой.

Рассмотрим алгоритмы перехода от одной формы к другой.

1. Симметричная → каноническая. Переход осуществляется путем добавления в левую часть каждого неравенства дополнительной неотрицательной переменной. Если неравенство было «≤», то балансовая переменная добавляется в левую часть неравенства со знаком «+». Если неравенство было «≥», то балансовая переменная добавляется в левую часть неравенства со знаком «–». Вводимые новые переменные называются балансовыми (базисными). Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) и используют, что min Z = –max (–Z).

2. Каноническая → симметричная. Для осуществления такого перехода находится общее решение системы уравнений – ограничений, целевая функция выражается через свободные переменные. Далее,воспользовавшисьнеотрицательностью базисных переменных, можно исключить их из задачи. Симметричная форма задачи будет содержать неравенства, связывающие только свободные переменные, и целевую функцию, зависящую только от свободных переменных. Значения базисных переменных находятся из общего решения исходной системы уравнений.

3. Общая → каноническая. Каждая переменная, на которую не было наложено условие неотрицательности, представляется в виде разности двух новых неотрицательных переменных. Неравенства преобразуются в уравнения путем введения в левую часть каждого неравенства балансовой переменной таким же образом, как это было описано при переходе от симметричной к канонической форме. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) таким же образом, как это было описано при переходе от симметричной к канонической форме.

Пример 1. Фирмой выпускаются колбасы пяти наименований: ветчинно-рубленная 1с, подольская 1с, особая 1с, деснянская 1с и баранья 2с. Определить максимальную прибыль фирмы от реализации колбасной продукции.

Ресурсы, которыми располагает фирма, ограничены.

Нормы расхода сырья, ресурсы жилованного мяса и прибыль от реализации 1ц готовой продукции заданы в таблице.

Виды сырья	Нормы расхода сырья (кг на 1 ц)	Ресурсы мяса, кг
x1	x2	x3	x4	x5
1.	Говядина 1с (ГЖ1)						58 621,0
2.	Говядина 2с (ГЖ2)						3568,9
3.	Свинина полужирная (СЖпж)						75362,0
4.	Свинина жирная (СЖ)						5006,9
5.	Баранина (БАР)						6851,9
6.	Сердце говяжье или свиное (СГ(с))						8536,4
7.	Шпик боковой (ШБ)						4965,1
8.	Крахмал пищевой (КП)						3812,5
9.	Белково-жировая эмульсия (Б/Жэ)						12865,0
Прибыль от реализации 1 ц готовой продукции, руб.	61,2	21,9	90,5	41,8	30,7

 

Решение. Строим математическую модель ЗЛП.

Введем обозначения переменных:

x₁ –ветчинно-рубленная 1с, ц

x₂ –подольская 1с, ц

x₃ –особая 1с, ц

x₄ –деснянская 1с, ц

x₅ –баранья 2с., ц

Построим план, удовлетворяющий условиям:

1. 40 x₁ +42 x₂ +32 x₃ +17 x₄ ≤ 58 621

2. 45x₄ + 30 x₅ ≤ 3568,9

3. 58 x₁ + 35 x₃≤ 74362

4. 55 x₂ +15 x₄ ≤5006,9

5. 10 x₃≤8436,4

6. 5 x₃+5 x₅ ≤4965,1

7. 2 x₁ +3 x₂ +3 x₄ +5 x₅ ≤3812,5

8. 15 x₃+20 x₄ ≤ 12865

9. x_i ≥0, i=

Целевая функция:

f(x)=62,1x₁+21,9x₂+90,5x₃ +41,8x₄+30,7x₅ →max

Все ограничения задачи представляют собой неравенства вида «≤», так как в условиях задачи сказано, что все ресурсы ограничены и использование дополнительных не предусмотрено.

1.2. Задание для самостоятельной работы. Построить математическую модель с использованием заданной экономической постановки.

1.1. Мебельная фабрика выпускает столы, стулья, бюро и книжные шкафы. При изготовлении этих товаров используются два различных типа досок, причем фабрика имеет в наличии 1500 м досок I типа и 1000 м досок II типа. Кроме того, задан объём трудовых ресурсов в количестве 800 чел.-ч. В следующей таблице приведены нормативы затрат каждого из видов ресурсов на изготовление единицы каждого изделия, а также получаемая прибыль.

 

Построить математическую модель определения ассортимента выпускаемой продукции таким образом, чтобы общая прибыль фабрикибыла максимальной.

1.2. Экспериментальная лаборатория химического завода разработала пять новых видов реактивов, которые имеют огромное значение в хозяйственной деятельности региона. Прибыль от продажи одной тонны реактива соответственно составляет 500, 800, 900, 100 и 1000 ден. ед. Но при производстве этих реактивов в атмосферу выделяются вредные вещества А, В и С. При этом нормы выбросов вещества А в месяц составляют 8000 мл, В – 1000 мл, С – 4000 мл. Выбросы этих веществ при производстве одной тонны реактива приведены в таблице.

Необходимо определить, в каком количестве данные реактивы можно производить, чтобы не превысить нормы выбросов вредных веществ иполучить максимальную прибыль.

1.3. При выращивании зерновых культур используются три вида удобрений в четырёх климатических зонах. Увеличение урожайности привнесении на 1 га 1 кг удобрения, запасы удобрений, а также площадьпосевных площадей каждой климатической зоны представлены в таблице.

Требуется распределить выделенный фонд удобрений между посевными зонами так, чтобы суммарный прирост урожайности зерновых культур за счёт внесения удобрений был максимальным.

1.4. На берегу Крымского побережья строится новая база отдыха «Аврора», которая будет состоять из корпусов «люкс», «высшего класса» и «среднего класса». Количество номеров в корпусах разного типа по предоставляемым услугам представлено в таблице.

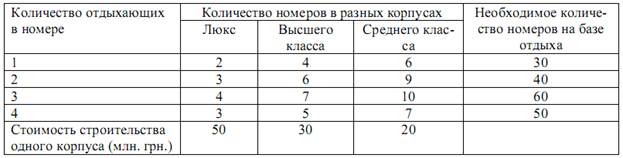
Необходимо определить оптимальный план строительства корпусов базы отдыха«Аврора» таким образом, чтобы затраты на строительство были минимальными.

1.5. Процесс изготовления глюкозы и патоки на крахмалопаточном комбинате представляет собой выполнение таких операций как расщепление сырья, выжимку и варение. Время работы оборудования при выполнении каждой операции ограничено и составляет соответственно 1600, 1200 и 1400 часов. Нормы времени обработки продукции при каждой операции, а также прибыль, получаемая комбинатом от реализации единицы продукции, приведены в таблице.

 

 

Необходимо определить план выпуска продукции, обеспечивающий комбинату максимальную прибыль.

1.6. На приобретение нового оборудования для открытия филиала фирма имеет в наличии 18 тыс. у.д.е., причем наличная производственная площадь составляет 28 м². Фирма может себе позволить содержать штат из 16 работников для обслуживания данного оборудования. На рынке представлено 2 вида подобного оборудования: более мощное, стоимостью 4 тыс. у.д.е., требующее 3 человека для обслуживания и производственную площадь 5 м². Данный вид оборудования позволяет производить 4 тыс. ед. продукции за смену. Второй вид оборудования, стоимостью 2,5 тыс. у.д.е., требует 2 человека для обслуживания и производственную площадь 7 м². Производственная мощность этого вида оборудования составляет 3

тыс. ед. продукции за смену.

Найти такой вариант приобретения оборудования, при котором филиал будет выпускать наибольшее количество продукции.

1.7. Для нормального развития промышленного рыбоводства в хозяйстве необходимо, чтобы ежедневно рыба получала 4 вида питательных веществ в количествах соответственно 20, 15, 18 и 12 тыс. ед. Эти питательные вещества содержатся в 2-х видах кормов. Содержание питательных веществ в одном кг корма приведено в следующей таблице:

Необходимо составить оптимальный рацион кормления рыб, если известно, что цена одного кг І вида корма 2 у.д.е., а ІІ вида – 1 у.д.е.

1.8. За счет мелиоративных работ площадь пашни в хозяйстве возросла на 120 га. Эту площадь было решено отвести под посев двух наиболее эффективных для хозяйства культур: проса и гречихи, причем гречихи необходимо получить не менее 1000 ц. В хозяйстве имеется 800 ц. минеральных удобрений. Выращивание культур характеризуется следующими показателями:

Найти такое распределения пашни под указанные культуры, при котором получаемая прибыль будет максимальной.

1.9. В саду имеются яблони различного возраста. Новый хозяин сада стоит перед дилеммой: имеющихся у него удобрений явно не хватает на подкормку всех яблонь. Известнаурожайность деревьев каждого возраста и количество удобрений, вносимых на одно дерево каждого возраста.

Необходимо найти оптимальное количество деревьев, которые должен удобрить хозяин, чтобы урожайность была максимальной. (Так как сад находится в нечернозёмной зоне, то неудобренные деревья практически не дают урожая).

1.10. Кондитерская фабрика для производства трёх видов карамели А, В и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида, общее количество сырья каждого вида, а также прибыль от реализации 1 т карамели данного вида приведены в таблице.

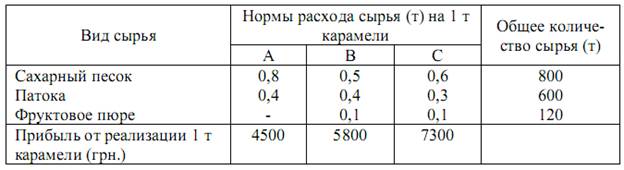
Найти план производства карамели, обеспечивающий максимальную прибыль от её реализации.

 

Поделиться:

Воспользуйтесь поиском по сайту: