 |
Иррациональные неравенства
|
|
|
|
Квадратные неравенства
Пример 6: Решить неравенство х2> 4
Решение:
х2> 4
(х - 2)∙(х + 2) > 0.
Решаем методом интервалов.
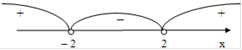
Рис. 1
Ответ: 
) Рациональные неравенства
Пример 7: Найти все целые значения, удовлетворяющие неравенству 
Решение:
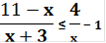
0;
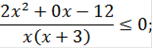
Методом интервалов:
Рис. 2
Решение неравенства: 
Целые числа, принадлежащие интервалу: -6;-5;-4;1.
Ответ:-6;-5;-4;1.
Иррациональные неравенства
Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8: Решить неравенство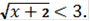 
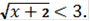
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
≤x<7.
Ответ: [-2;7)/
) Показательные, логарифмические неравенства
Пример 9: Решите неравенство 
..
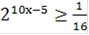Решение:
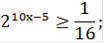
x 
Ответ: x 
Пример 10: Решите неравенство 
.
Решение:
;
+5x+1>1;
+5x>0;
x(2x+5)>0 
.
Ответ: 
.
Особенности решения уравнения с параметрами
Рассмотрим уравнение
F(х,у,...,z;б,в,...,г)=0 (1)
с неизвестными х, у,..., z и с параметрами б,в,..., г;при всякой допустимой системе значений параметров б0,в0,..., г0 уравнение (1) обращается в уравнение
F(х,у,...,z;б0,в0,...,г0)=0 (2)
с неизвестными х, у,..., z, не содержащее параметров. Уравнение (2) имеет некоторое вполне определенное множество решений.
Решить уравнение содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения.
Основные виды уравнений с параметрами:
) Линейные и квадратные уравнения, содержащие параметр
Линейные и квадратные уравнения, содержащие параметр, можно объединить в одну группу - группу уравнений с параметром не выше второй степени.
|
|
|
Уравнения с параметром не выше второй степени являются самыми распространенными в практике итоговых и конкурсных заданий. Их общий вид определяется многочленом.
Контрольные значения параметра определяются уравнением. На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.
Тогда решением всякого уравнения с параметром не выше второй степени осуществляется по следующим этапам:
. На числовой прямой отмечаются все контрольные значения параметра, для которых соответствующие частные уравнения не определены.
. На области допустимых значений параметра исходного уравнения при помощи равносильных преобразований приводится к виду.
. Выделяют множество контрольных значений параметра, для которых уравнение имеет конечное множество решений, то для каждого найденного контрольного значения параметра соответствующее частное уравнение решается отдельно.
Проводится классификация частных уравнений по первым трем типам. На бесконечном множестве решений уравнения проводится решение уравнения, выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых и, соответствует третий тип не особых частных уравнений.
. Выделяются контрольные значения параметра, для которых дискриминант обращается в нуль. Соответствующие не особые частные уравнения имеют двукратный корень.
. Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков определяется знак дискриминанта.
) Дробно-рациональные уравнения, содержащие параметр, сводящиеся к линейным.
|
|
|
Процесс решения дробно-рациональных уравнений протекает по обычной схеме: данное уравнение заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего учащиеся решают известным им способом целое уравнение, исключая посторонние корни, то есть числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы посторонние корни исключить, требуется находить значение параметра, обращающее общий знаменатель в нуль, то есть решать соответствующие уравнения относительно параметра.
) Иррациональные уравнения, содержащие параметр.
Главными особенностями при решении уравнений такого типа являются:
.ограничение области определения неизвестной х, так как она меняется в зависимости от значения параметра;
. в решении уравнений вида при возведении в квадрат необходимо учитывать знак и проводить проверку корней.
При рассмотрении всех особых случаев и возведении обеих частей иррационального уравнения в квадрат мы переходим к решению квадратного уравнения с параметром.
) Показательные уравнения, содержащие параметр.
Большинство показательных уравнений с параметрами сводится к показательным уравнениям вида: аf(x) = bg(х), где а>0, b>0.
Область допустимых значений такого уравнения находится как пересечение областей допустимых значений функций f(x) и g(х). Для решения уравнения аf(x) = bg(х) необходимо рассмотреть следующие случаи:
. При а=b=1 решением уравнения аf(x) = bg(х) является область его допустимых значений D.
. При а=1, b≠1 решением уравнения аf(x) = bg(х) служит решение уравнения g(х)=0 на области допустимых значений D.
. При а≠1, b=1 решение уравнения аf(x) = bg(х) находится как решение уравнения f(х) = 0 на области D.
. При а=b (а>0, а≠1, b>0, b≠1) уравнение аf(x) = bg(х) равносильно уравнению f(х) = g(х) на области D.
. При а≠b (а>0, а≠1, b>0, b≠1) уравнение аf(x) = bg(х) тождественно уравнению (c>0, c≠1) на области D.
) Логарифмические уравнения, содержащие параметр.
Решение логарифмических уравнений с параметрами сводится к нахождению корней элементарного логарифмического уравнения.
Важным моментом решения уравнений такого типа является проверка принадлежности найденных корней ОДЗ исходного уравнения.
|
|
|
Основные методы решения уравнений, содержащих параметр:
. Аналитический метод
.Свойства функций в задачах, содержащих параметр. Функциональный подход.
. Графический метод. Координатная плоскость (x;y).
. Графический метод. Координатная плоскость (x;a).
Особенности решения неравенства с параметрами
Неравенство с параметрами - математическое неравенствовнешний вид и решение которого зависит от значений одного или нескольких параметров. Как при решении уравнения, так и при решении неравенства требуется найти все те значения неизвестной величины, для каждого из которых указанное соотношение оказывается верным.
Решение неравенства (уравнения) может включать в себя несколько методов решения, соответствующих каждому виду уравнения при определенных значениях параметра. Например, при каком-то значении параметра неравенство линейное, поэтому решаем его аналитически тождественными преобразованиями; при остальных значениях параметра неравенство квадратичное, - решаем его функционально-графическим способом.
Аналогично уравнениям с параметрами, неравенства с параметрами имеют ту же классификацию видов и методов решения.
) Линейные и квадратные неравенства, содержащие параметр
) Дробно-рациональные неравенства, содержащие параметр, сводящиеся к линейным.
Решение некоторых дробно-рациональных неравенств сводится к решению неравенств первой или второй степени.
) Иррациональные неравенства, содержащие параметр.
) Показательные неравенства, содержащие параметр.
) Логарифмические неравенств, содержащие параметр.
Основные методы решения неравенств, содержащих параметр:
. Аналитический метод
.Свойства функций в задачах, содержащих параметр. Функциональный подход.
. Графический метод. Координатная плоскость (x;y).
. Графический метод. Координатная плоскость (x;a).
2. Методические рекомендации к решению уравнений и неравенств с параметрами
Решение задач с параметрами является одним из самых трудных разделов школьной математики. При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить довольно разветвленные логические построения, аккуратность и внимательность для того, чтобы не потерять решений и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры, но, в свою очередь, эти задачи сами способствуют их развитию. Опыт вступительных экзаменов показывает, что учащиеся, владеющие методами их решения, обычно успешно справляются и с другими задачами.
|
|
|
К сожалению, в программах по математике для неспециализированных школ задачам с параметром практически не отводится места, а, например, в учебнике для учащихся школ и классов с углубленным изучением курса математики («Алгебра и математический анализ для 10 и 11 классов», Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд) им отведено место только в 11-м классе. Между тем, задачи с параметрами можно и нужно использовать уже начиная с линейных и квадратных уравнений и неравенств. Это могут быть задачи нахождения решений в общем виде, определения корней, удовлетворяющих каким-либо свойствам, исследования количества корней в зависимости от значений параметра. Так сделано в «Сборнике задач по алгебре для 8-9 классов», 1994 г. (авторы: М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич). Важно, чтобы школьники уже на первых простых примерах усвоили: во-первых, необходимость аккуратного обращения с параметром - фиксированным, но неизвестным числом, поняли, что оно имеет двойственную природу (с одной стороны, это некоторое число, с другой стороны, степень свободы общения с ним ограничивается его неизвестностью); во-вторых, что запись ответа существенно отличается от записи ответов аналогичных уравнений и неравенств без параметра.
Методически было бы правильно каждый пройденный тип уравнений (неравенств) завершать задачами с использованием параметра. Во-первых, школьнику трудно привыкнуть к параметру за два-три занятия - нужно время; во-вторых, использование подобных задач улучшает закрепление пройденного материала; в-третьих, оно способствует развитию его математической и логической культуры, а также развитию интереса к математике, поскольку открывает перед ним новые методы и возможности для самостоятельного поиска.
Понятие параметра является математическим понятием, которое часто используется в школьном курсе математики и в смежных дисциплинах.
класс - при изучении линейной функции и линейного уравнения с одной переменной.
класс - при изучении квадратных уравнений.
|
|
|
Общеобразовательная программа школьного курса математики не предусматривает решение задач с параметрами, а на вступительных к заменах в вузы и на ЕГЭ по математике задачи с параметрами присутствуют, решение которых вызывает большие затруднения учащихся.Задачи с параметрами обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности.
При решении уравнения (неравенства) можно пользоваться следующим алгоритмом.
Алгоритм решения уравнения или неравенства с параметром
1. Определяют ограничения, налагаемые на значения неизвестного 
и параметра, вытекающие из того, что функции и арифметические операции в 
или 
имеют смысл.
. Определяют формальные решения, записываемые без учета ограничений. Если при решении возникают контрольные значения параметра, то их наносят на числовую ось 
. Эти значения разбивают область допустимых значений параметра на подмножества. На каждом из подмножеств решают заданное уравнение..
. Исключают те значения параметра, при которых формальные решения не удовлетворяют полученным ограничениям.
. На числовую ось . добавляют значения параметра, найденные в п.3. Для каждого из промежутков на оси . записывают все полученные решения в зависимости от значений параметра 
. (В случае достаточно простых уравнений п.4 можно опустить).
. Выписывают ответ, т.е. записывают решения в зависимости от значений параметра .
Наличие параметра в задаче предполагает специальную форму записи ответа, позволяющую установить, каков ответ для любого допустимого значения параметра. Недопустимые значения также указываются в ответе, и считается, что при этих значениях параметра задача не имеет решения. При записи ответа обычно значения параметра перечисляются в порядке возрастания от −∞ до +∞, но иногда для компактности ответа объединяют промежутки для параметра, на которых формулы решения совпадают.
В случае ветвления решения удобно использовать числовую прямую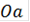 
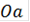., на которую наносятся контрольные значения параметра, а на промежутках, на которые эти значения разбили прямую, указываются ответы задачи. Данный прием позволяет в дальнейшем не потерять найденные ответы и четко указать значения параметра, которым они соответствуют.
Продемонстрируем сказанное выше на примере.
Пример 10: Решить неравенство 
.
Решение:
Контрольные значения параметра получаются из условия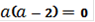 
, так как при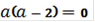 
неравенство не содержит переменной x.
Нанесем на числовую ось Oa контрольные значения. Они разбивают ось Oa на промежутки:
) a<0; 2) 0< a <2; 3) a>2
На каждом из этих промежутков решим данное неравенство. Значения a=0 и. a=2 требуют отдельного рассмотрения.
Если a<0, то a(a-2)>0. Разделив обе части неравенства на множитель a(a − 2) ≠ 0, получим x> 
.
Если 2>a>0, a(a − 2) < 0 и, следовательно, x< .
Если a>2, a(a − 2) > 0 и x> /
Нанесем получаемые в ходе решения ответы на соответствующие промежутки числовой оси Oa и запишем ответ.
Промежуток, к которому относится соответствующее решение, помечается на рисунке дугой. На ее конце ставится стрелочка в том случае, если это решение не относится к крайней точке промежутка.
Рис. 3
Ответ: Если a<0, то x> ; если 0<a<2, то x< ; если a>2, то x> 
; если a=0 и a=2, то решений нет.
Главная особенность задач с параметрами - ветвления решения в зависимости от значений параметров. Другими словами, процесс решения осуществляется классификаций частных уравнений (неравенств) по типам с последующим поиском решений каждого типа.
Одновременно решение бесконечной совокупности частных уравнений и неравенств с учетом требования равносильности преобразований возможно лишь при развитии достаточного уровня логического мышления. С другой стороны, формирование методов решения уравнений и неравенств с параметрами обеспечивает значительный процесс в развитии математической культуры учащихся. Развивающий характер уравнений и неравенств с параметрами определяется их способностью реализовывать многие виды мыслительной деятельности учащихся:
. Выработка определенных алгоритмов мышления.
. Умение определить наличие и количество корней в уравнении.
. Решение семейств уравнений, являющихся следствием данного.
. Выражение одной переменной через другую.
. Нахождение области определения уравнения.
. Повторение большого объема формул при решении.
. Значение соответствующих методов решения.
. Широкое применение словесной и графической аргументации.
. Развитие графической культуры учащихся.
Все вышесказанное позволяет говорить о необходимости изучения решений задач с параметрами.
уравнение неравенство параметр
Заключение
Таким образом, в нашей курсовой работе речь шла о уравнениях и неравенствах с параметрами в школьном курсе математике, особенности их решения. Были рассмотрены уравнения и неравенства в школьном курсе математике, особенности решения уравнений и неравенств с параметрами.Была разработана методики к решению уравнений и неравенств с параметрами.
Цель нашей курсовой работы заключалась в выявление видов, методов решения уравнений и неравенств с параметрами.
Для достижения данной цели, была подобрана и изучена литература по данной проблеме, исследовано особенности решения уравнений и неарвенств с параметрамишкольном курсе математики основной школы, представлена методические рекомендации к решению уравнений(неравенств) с параметрами.
Вывод: Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты. В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.
Изучение уравнений и неравенств с параметрами в общеобразовательных школах дает учащимся большие возможности для анализа различных ситуаций, то есть показывает значимость этих понятий при решении многих практических задач. Именно с простейших практических задач и приложений математически постепенно формируется у школьников понимание значимости математики в жизни.
Список используемой литературы
уравнение неравенство математика
1. Алгебра. 7 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2010.
2. Алгебра. 7 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2010.
3. Алгебра. 7 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011.
. Алгебра. 8 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2012.
. Алгебра. 8 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2011.
. Алгебра. 8 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011.
. Алгебра. 9 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2013.
. Алгебра. 9 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2013.
. Алгебра. 9 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011.
. Алгебра. Учеб.для 7 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2011.
. Алгебра. Учеб.для 7 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2012.
. Алгебра. Учеб.для 8 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2014.
. Алгебра. Учеб.для 8 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2011.
. Алгебра. Учеб.для 9 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2010.
. Алгебра. Учеб.для 9 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2001.
. Беляева Э.С. Математика. Уравнение и неравенство с параметрами в 2 ч.: Учебное пособие/ Беляева Э.С., Потапов А.С., Титоренко С.А. -., - М.:,2009.
. Крамор В.С. Задачи с параметром и методы их решения: Учебное пособие /- М.: Оникс; Мир и Образование,2007
. Козко А.И. Задачи с параметрами и другие сложные задачи: Учебное пособие для вузов/Козко А. И.,Чирский В. Г. - М.:,МЦНМО,2007.
. Мирошин В.В. Решение задач с параметрами. Теория и практика: Учебное пособие /. - М.: Экзамен,2009.
. Прокофьев А.А. Задачи с параметрами: Учебное пособие. - М.: МИЭТ, 2004.
. Севрюков П.Ф. Школа решения задач с параметрами: Учебное пособие /Севрюков П.Ф., Смоляков А. Н.-2-е изд.- М.:,2009.
|
|
|
